More than 5 years have passed since last update.

正規表現のJITコンパイラを実装する

Last updated at 2016-02-01Posted at 2015-05-16

前回の記事で、正規表現（の抽象構文木）からLLVMの中間表現（LLVM IR）¹へコンパイルするという試みを行ったところ、Twitterで次のような投稿をいただいた²。

@_yyu_ https://t.co/UPV535fqbB とかを使うと、Mokkosuから動的コード生成ができてきっと楽しいです。
— ラムダ太郎 (@lambdataro) 2015, 5月 11

つまり、プログラムの実行時に正規表現に対応するバイトコードを生成して、それを実行すれば速度が早くなったりするかもしれないということである。これは一般的にJust in Time（JIT）コンパイルと呼ばれているもので、正規表現技術入門という本でも紹介されている。Mokkosuで実装してもよかったが、たぶんMokkosuのプログラマはそれほど多くないだろうということで、今回もScalaを使って実装することにする。

正規表現の抽象構文木

今回も正規表現の抽象構文木を次のデータ型で表現する。

sealed trait Regex
case object Empty                  extends Regex
case class Let(c: Char)            extends Regex
case class Con(a: Regex, b: Regex) extends Regex
case class Alt(a: Regex, b: Regex) extends Regex
case class Star(a: Regex)          extends Regex

動的コード生成の方法

JVMのバイトコード（バイナリ）を生成するコンパイラを自力で作るというのも一興だったが、色々調べた結果、ASMというフレームワークを使えば気軽に動的コード生成ができそうな気がしたので、この記事ではこのフレームワークを用いて実行時にバイトコードを動的生成する。
ただ、この記事ではこのフレームワークについての知識は特に必要ない。

バイトコードの中間表現

今回も前回と同じように、バイトコードを表現するデータ型を定義して、それを後でバイトコードへ変換するアプローチを取る。バイトコードに対応するこれらの表現のことをこの記事では中間表現と呼ぶ。

sealed trait LId
case class LInt(n: Int)   extends LId
case class LLbl(l: Label) extends LId

sealed trait Repr
case object Const1          extends Repr
case class  Push(n: Int)    extends Repr
case object Dup2            extends Repr
case class  Lbl(l: LId)     extends Repr
case object Add             extends Repr
case class  Goto(l: LId)    extends Repr
case class  IfTrue(l: LId)  extends Repr
case class  IfCmpNe(l: LId) extends Repr
case class  InvokeStatic(p: String, n: String, t: String)  extends Repr
case class  InvokeVirtual(p: String, n: String, t: String) extends Repr

まずLIdはラベルの識別子を表現するデータ型であり、Repr³はJVMの命令を表現するデータ型である。
最小の正規表現をコンパイルするだけならば、これだけの命令で済むというのは少し興味深い。

\def\AtSOne#1\csod{%
	\begin{array}{c|}
		\hline
		#1\\
		\hline
	\end{array}
}%
\def\AtSTwo#1,#2\csod{%
	\begin{array}{c|c|}
		\hline
		#1 & #2\\
		\hline
	\end{array}
}%
\def\AtSThree#1,#2,#3\csod{%
	\begin{array}{c|c|c|}
		\hline
		#1 & #2 & #3\\
		\hline
	\end{array}
}%
\def\AtSFour#1,#2,#3,#4\csod{%
	\begin{array}{c|c|c|c|}
		\hline
		#1 & #2 & #3 & #4\\
		\hline
	\end{array}
}%
\def\AtSFive#1,#2,#3,#4,#5\csod{%
	\begin{array}{c|c|c|c|c|}
		\hline
		#1 & #2 & #3 & #4 & #5\\
		\hline
	\end{array}
}%
\def\SOne#1{\AtSOne#1\csod}
\def\STwo#1{\AtSTwo#1\csod}
\def\SThree#1{\AtSThree#1\csod}
\def\SFour#1{\AtSFour#1\csod}
\def\SFive#1{\AtSFive#1\csod}
\def\textsc#1{\dosc#1\csod}
\def\dosc#1#2\csod{{\rm #1{\scriptsize #2}}}
\def\red#1{\color{red}{#1}}
\def\blue#1{\color{blue}{#1}}

スタックに関する表記

JVMは一本のスタックにデータを出し入れして計算を進めていく構造を取っている。この記事では分かりやすさのために、スタックに入ったデータを次のように表す。

\SFive{\red{s},\blue{t},a,c,k}

ここから、例えばスタックの先頭を破棄する命令 $\textsc{POP}$ を行うと、次のようにスタックが変化する。

\SFive{\red{s},\blue{t},a,c,k} \Rightarrow \SFour{\blue{t},a,c,k}

そして、スタックの先頭にデータを加える命令 $\textsc{PUSH}(\red{c})$ を行うと、次のようにスタックが変化する。

\SFour{\blue{t},a,c,k} \Rightarrow \SFive{\red{c},\blue{t},a,c,k}

また、空のスタックを次のように表す。

\SOne{\phantom{a}}

正規表現から中間表現への変換

前回の記事ではレジスタを用いるLLVMの特性上、レジスタの番号をコンパイラが管理しなければならず、コードが必要以上に複雑になってしまった。ところがJVMは一本のスタックを操作するスタックマシンとなっているので、前回のコードより少しシンプルになっている。
また、今回も前回と同様に正規表現技術入門やRegular Expression Matching: the Virtual Machine Approachで紹介されたていたVMをバイトコードで表現するアプローチとなる。
そして、次のような型を持つ関数を生成する。

public static boolean test(String str, int sp, int label)

実装の方針

生成された関数testは次の動作を行う。

引数str, sp, labelを受け取る
引数を全てスタックへ置く（$\textsc{LOAD}$）$\SOne{\phantom{a}} \Rightarrow \SThree{label, sp, str}$
labelの値に応じてジャンプする（$\textsc{LOOKUPSWITCH}$）$\SThree{label, sp, str} \Rightarrow \STwo{sp, str}$
ジャンプ先の処理を実行する

なので、ジャンプ先の処理に入る際のスタックは$\STwo{sp, str}$という状態になっている。

文字

case Let(c) =>
  val (l1, n1) = mk_label(n)
  val r = List(
    Lbl(l1),
    Dup2,
    InvokeVirtual("java/lang/String", "charAt", "(I)C"),
    Push(c.toInt),
    IfCmpNe(lmiss),
    Const1,
    Add
  )
  (r, n1)

これは次のような処理を中間表現を生成する。なお、lmissとはマッチに失敗した場合に遷移する場所である。

ラベルを打つ
スタックの二つをコピーする（$\textsc{DUP2}$）$\STwo{sp, str} \Rightarrow \SFour{sp, str, sp, str}$
charAtを呼び出す（$\textsc{INVOKEVIRTUAL}$）charAtは文字列strと位置$i$という二つの引数を取り、strの位置$i$にある文字をスタックの先頭に置く $\SFour{sp, str, sp, str} \Rightarrow \SThree{char, sp, str}$
c に対応する文字コード（c.toInt）をスタックの先頭に置く（$\textsc{PUSH}$）$\SThree{char, sp, str} \Rightarrow \SFour{c, char, sp, str}$
スタックの先頭と二番目が等しくなければlmissへジャンプする（$\textsc{IFCMPNE}$）$\SFour{c, char, sp, str} \Rightarrow \STwo{sp, str}$
スタックの先頭に$1$を置く（$\textsc{CONST1}$）$\STwo{sp, str} \Rightarrow \SThree{1, sp, str}$
スタックの先頭と二番目を足し算して、結果を先頭に置く（$\textsc{ADD}$）$\SThree{1, sp, str} \Rightarrow \STwo{sp + 1, str}$

連接

case Con(a, b) =>
  val (r1, n1) = loop(a, n)
  val (r2, n2) = loop(b, n1)
  (r1 ++ r2, n2)

前の部分と後の部分をそれぞれ中間表現へ変換し、それを結合する。

選択

case Alt(a, b) =>
  val (l1, n1) = mk_label(n)
  val (r1, n2) = loop(a, n1)
  val (l2, _)  = mk_label(n2)
  val (r2, n3) = loop(b, n2)
  val (l3, _)  = mk_label(n3)
  val r = List(
    Lbl(l1),
    Dup2,
    Push(n1),
    InvokeStatic(cname, mname, mtype),
    IfTrue(lmatch),
    Goto(l2)) ++
    r1 ++ (Goto(l3) :: r2)
  (r, n3)

まず、事前に次の処理を行う。

部分正規表現aを中間表現へ変換する（これをr1とする）
r1の末尾に次の命令を加える

選択のもう一方（部分正規表現b）をスキップする（$\textsc{GOTO}$）

部分正規表現bを中間表現へ変換する（これをr2とする）

そして、次のような処理を中間表現を生成する。なおlmatchはマッチに成功した際に遷移する場所である。

ラベルを打つ
スタックの二つをコピーする（$\textsc{DUP2}$）$\STwo{sp, str} \Rightarrow \SFour{sp, str, sp, str}$
r1の先頭を指すラベルn1をスタックの先頭に置く（$\textsc{PUSH}$）$\SFour{sp, str, sp, str} \Rightarrow \SFive{n_1, sp, str, sp, str}$
関数testを再帰的に呼び出し、返り値をスタックの先頭に置く（$\textsc{INVOKESTATIC}$）$\SFive{n_1, sp, str, sp, str} \Rightarrow \SThree{{1, {\rm or}, 0}, sp, str}$
スタックの先頭が$1$ならば、lmatchへジャンプする（$\textsc{IFTRUE}$）$\SThree{{1, {\rm or}, 0}, sp, str} \Rightarrow \STwo{sp, str}$
r2の先頭を指すラベルl2へジャンプする（$\textsc{GOTO}$）
生成したr1とr2を結合する

繰り返し

case Star(Star(a)) => loop(Star(a), n)

case Star(a) =>
  val (l1, n1) = mk_label(n)
  val (r1, n2) = loop(a, n1)
  val (l2, n3) = mk_label(n2)
  val r2       = List(Lbl(l2), Goto(l1))
  val (l3, _)  = mk_label(n3)
  val r = List(
    Lbl(l1),
    Dup2,
    Push(n1),
    InvokeStatic(cname, mname, mtype),
    IfTrue(lmatch),
    Goto(l3)) ++
    r1 ++ r2
  (r, n3)

まず、事前に次の処理を行う。

部分正規表現aを中間表現へ変換する（これをr1とする）
r1の末尾に次の処理をする中間表現を加える
ラベルを打つ
ラベルl1（後で定義）へジャンプする（$\textsc{GOTO}$）

そして、次のような処理を中間表現を生成する。

ラベルを打つ（このラベルをl1とする）
スタックの二つをコピーする（$\textsc{DUP2}$）$\STwo{sp, str} \Rightarrow \SFour{sp, str, sp, str}$
r1の先頭を指すラベルn1をスタックの先頭に置く（$\textsc{PUSH}$）$\SFour{sp, str, sp, str} \Rightarrow \SFive{n_1, sp, str, sp, str}$
関数testを再帰的に呼び出し、返り値をスタックの先頭に置く（$\textsc{INVOKESTATIC}$）$\SFive{n_1, sp, str, sp, str} \Rightarrow \SThree{{1, {\rm or}, 0}, sp, str}$
スタックの先頭が$1$ならば、lmatchへジャンプする（$\textsc{IFTRUE}$）$\SThree{{1, {\rm or}, 0}, sp, str} \Rightarrow \STwo{sp, str}$
次の場所へジャンプする（$\textsc{GOTO}$）
生成した中間表現r1を結合する

中間表現からバイトコードの生成

前回の記事と同じように、中間表現のパターンマッチで次のように実装できる。

def repr_to_code(mv: MethodVisitor, r: Repr, la: List[Label]): Unit = r match {
  case Lbl(l) => mv.visitLabel(get_label(l, la))
  case Const1 => mv.visitInsn(ICONST_1)
  case Push(n) => mv.visitIntInsn(BIPUSH, n)
  case Add => mv.visitInsn(IADD)
  case Dup2 => mv.visitInsn(DUP2)
  case Goto(l) => mv.visitJumpInsn(GOTO, get_label(l, la))
  case IfCmpNe(l) => mv.visitJumpInsn(IF_ICMPNE, get_label(l, la))
  case IfTrue(l) => mv.visitJumpInsn(IFNE, get_label(l, la))
  case InvokeVirtual(p, n, t) => mv.visitMethodInsn(INVOKEVIRTUAL, p, n, t)
  case InvokeStatic(p, n, t) => mv.visitMethodInsn(INVOKESTATIC, p, n, t)
}

実装

今回の実装はGithubで公開している。

ベンチマーク

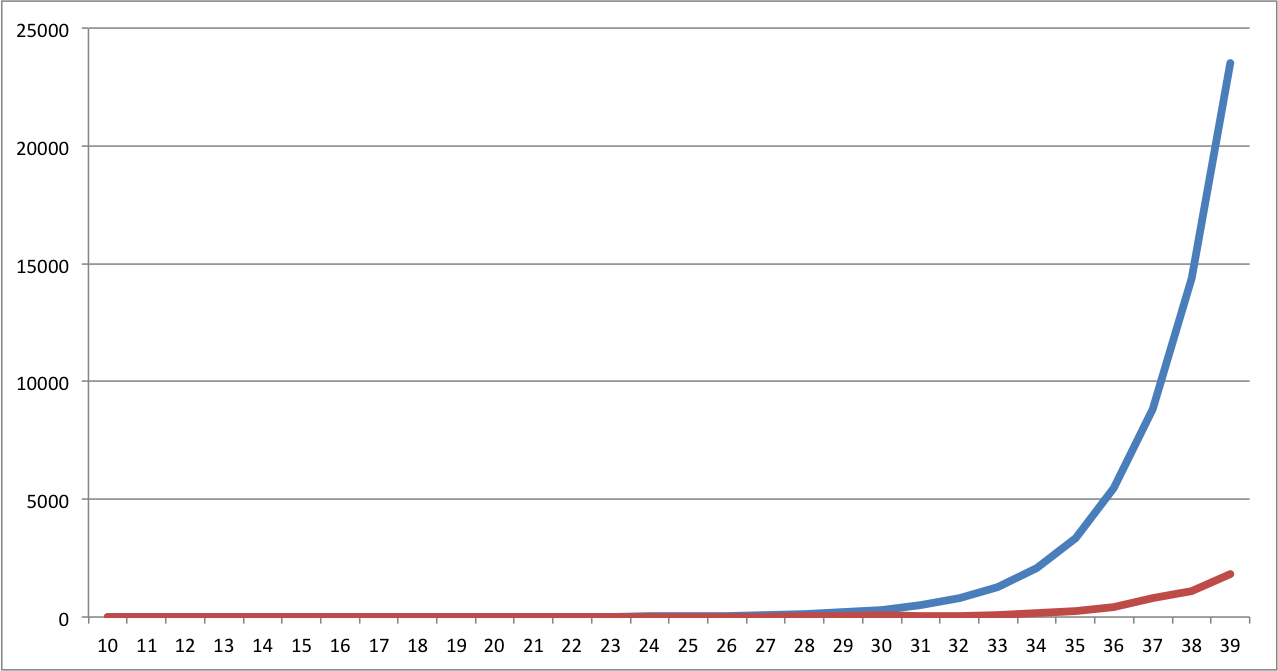
遅い正規表現の方おもしろいような気がするので、遅いッ！遅すぎるッ！Java の正規表現のお話。から遅い正規表現の例を紹介する⁴。

(aa|a)*X

与える文字列は a や aaaaa といったマッチしない文字列を使って、マッチしないと判定するまでにかかる時間を測定することとする。次のコードを用いて、文字列 a を10文字から一文字ずつ増やして、かかる時間（ミリ秒）を計測した。

for (i <- 10 to 40) {
  var str = ""
  for (_ <- 1 to i) {
    str += "a"
  }
  str += "\0"

  var time = 0.0
  for (_ <- 1 to 10) {
    val start = System.currentTimeMillis
    m.invoke(c, str, Int.box(0), Int.box(0))
    //p.findFirstIn(str)
    time += (System.currentTimeMillis - start)
  }
  println(time / 10 + ",")
}

結果

グラフの赤が今回実装したエンジンで、青がScalaの正規表現エンジンである。

Scalaの正規表現エンジンと比べて、少なくともこの例においてはよいパフォーマンスが得られた。

まとめ

今回作成したコードは約200行程度であり、動的コード生成をシンプルに実装できたうえに、パフォーマンスが実際に向上したのは大変よかった。もちろん、この正規表現は最小の機能しか持っていないため、直ちにこのエンジンが有用かというとそうではないだろう。

参考文献

前回の記事では統一的に「機械語」という表現を用いていたが、より正確な表現ではLLVMの中間表現（LLVM IR）であるので、この記事ではこちらで記述する。 ↩
会話に登場する“Mokkosu”とはプログラム言語Mokkosuのことである。 ↩
前回は「命令（Instruction）」という意味でInstという名前にしたが、「命令の表現（Representation）」であること強調するために今回はReprという名前にした。 ↩
今回実装した正規表現は機能が小さすぎて、記事にある正規表現を実行できないので、少々アレンジしたもの用いることにする。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up