概要
Haskell には Co/Yonda 型があり、圏論には米田の補題がある。両者の関連についての分かりやすい解説を見つけられなかったため、ここで米田の補題と Co/Yoneda 型をシームレスに繋ぐことを試みる。
圏論の基礎知識は仮定している。また Co/Yoneda 型は kan-extensions で定義されたものを参照している。
記法
圏論の記法は一般的なものを用いるが、Haskell コードとの比較のし易さのために、圏 $\mathcal C$ における対象 $A$ から対象 $B$ への射の集合 $\mathcal C (A,B)$ を
$$
A\underset{\mathcal C}{\rightarrow}B
$$
とも書くことにする。
米田の補題
米田の補題によると、圏 $\mathcal C$ とその対象 $A$ ならびに関手 $F:\mathcal C\rightarrow \mathcal{Sets}$ について
$$
[\mathcal C,\mathcal{Sets}](\mathcal C(A,-),F)\simeq FA \qquad (0)
$$
が成り立つ。
すると自然変換の定義より、圏 $\mathcal C$ の任意の対象 $B$ について
$$
FA\overset{\omega_B}{\rightarrow} \mathcal{Sets}(C(A,B),FB)
$$
なる射の存在が言える。記法を変えると次の通りである。
$$
FA\overset{\omega_B}{\rightarrow} \left[\left(A\underset{\mathcal C}{\rightarrow}B\right)\underset{\mathcal{Sets}}{\longrightarrow}FB)\right]\qquad(1)
$$
$B=A$ のとき、逆向きの射
$$
FA\overset{\eta_A}{\leftarrow}\left[\left(A\underset{\mathcal C}{\rightarrow}A\right)\underset{\mathcal{Sets}}{\longrightarrow}FA)\right]
\qquad(2)
$$
を
$$
\eta_A(f)=f(\mathrm{id}_A)
$$
によって構成することができる。
Yoneda型
Yoneda 型は次のように定義される。
newtype Yoneda f a = Yoneda { runYoneda :: forall b. (a -> b) -> f b }
すなわち Yoneda f a は (a -> b) -> f b 型のシノニムであり、b の型は任意に取れる。
この型はちょうど (1) 式の右辺そのものである。
Data.Functor.Yoneda で定義されている liftYoneda
liftYoneda :: Functor f => f a -> Yoneda f a
liftYoneda a = Yoneda (\f -> fmap f a)
は (1) 式の射 $\omega_B$ そのものの実装である。また、lowerYoneda
lowerYoneda :: Yoneda f a -> f a
lowerYoneda (Yoneda f) = f id
は (2) 式の射 $\eta_A$ そのものである。
余米田の補題
(1) 式をuncurrying すると、任意の対象 $B$ について
$$
FA\times \left(A\underset{\mathcal C}{\rightarrow}B\right) \overset{\omega^B}{\rightarrow} FB
$$
なる射 $\omega^B$ が得られる。この射の存在は同型
$$
F\otimes_{\mathcal C}\mathcal C(-,B)\simeq FB
$$
で言い換えることができ、余米田の補題と呼ぶ。
記号を合わせるために $A$ と $B$ とを入れ替えて
$$
\left(B\underset{\mathcal C}{\rightarrow}A\right)\times FB \overset{\omega^A}{\rightarrow} FA
\qquad(3)
$$
としよう。やはり $B=A$ のとき、逆向きの射
$$
\left(A\underset{\mathcal C}{\rightarrow}A\right)\times FA \overset{\eta^A}{\leftarrow} FA
\qquad(4)
$$
が
$$
\eta^A(a)=(\mathrm{id}_A,a)
$$
で構成できる。
Coyoneda型
Coyoneda型は次のように定義される。
data Coyoneda f a where
Coyoneda :: (b -> a) -> f b -> Coyoneda f a
これは
data Coyoneda f a = forall b. Coyoneda (b -> a) (f b)
と書いても同じことである。すなわち Coyoneda 型 Coyoneda f aは (b -> a) 型の関数と f b 型の値を保持する型であり、b の型は任意に取れる。
これは(3)式の左辺そのものである。
Data.Functor.Coyoneda で定義されている lowerCoyoneda
lowerCoyoneda :: Functor f => Coyoneda f a -> f a
lowerCoyoneda (Coyoneda f m) = fmap f m
は (3) 式の射 $\omega^A$ そのものの実装である。また liftCoyoneda
liftCoyoneda :: f a -> Coyoneda f a
liftCoyoneda = Coyoneda id
は (4) 式の射 $\eta^A$ そのものである。
結論
米田の補題と Co/Yoneda 型の定義との対応をごく自然に取ることができた。
備考
end と忍者米田の補題
上で行った米田の補題の書き換えは、end を用いると
$$
\begin{split}
F &\simeq \int_{C\in\mathcal C}\mathcal{Sets}(\mathcal{C}(-,C),FC)
\\
F&\simeq\int^{C\in\mathcal C}FC\times\mathcal C(C,-)
\end{split}
$$
と定式化できる。これらを忍者米田の補題と呼ぶ。上で$\omega$ と書いた射は co/wedge である。
なお、ここで述べているのはすべで共変版であり、反変版も当然存在する。
Kan 拡張との関連
忍者米田の補題は Kan 拡張を用いて
$$
F\simeq \mathrm{Ran}_{\mathrm{id}} F , \quad F\simeq \mathrm{Lan}_{\mathrm{id}} F
$$
と書くこともできる。それゆえにこれらの型は kan-extensions で定義されており、相互の変換関数が次のように定義されている。
yonedaToRan :: Yoneda f a -> Ran Identity f a
yonedaToRan (Yoneda m) = Ran (m . fmap runIdentity)
ranToYoneda :: Ran Identity f a -> Yoneda f a
ranToYoneda (Ran m) = Yoneda (m . fmap Identity)
coyonedaToLan :: Coyoneda f a -> Lan Identity f a
coyonedaToLan (Coyoneda ba fb) = Lan (ba . runIdentity) fb
lanToCoyoneda :: Lan Identity f a -> Coyoneda f a
lanToCoyoneda (Lan iba fb) = Coyoneda (iba . Identity) fb
Functor とすることについて
Co/Yoneda 型は Functor 型クラスのインスタンスとすることができる。実際、kan-extensionsでは
instance Functor (Yoneda f) where
fmap f m = Yoneda (\k -> runYoneda m (k . f))
instance Functor (Coyoneda f) where
fmap f (Coyoneda g v) = Coyoneda (f . g) v
と定義されている。これを少し読み解いてみよう。
まず Coyoneda 型は、単純に (b -> a) 型の関数と f b 型の値を保持するデータ型なのであった。射を fmap で Coyoneda 型に持ち上げて適用しても、射の結合を行うだけで、値への適用は行わない。fmap したフリをする。ほんとうに fmap するには lowerCoyoneda で Coyoneda 型を剥いでやらねばならない。
有名な記事に倣ってこの様子を戯画してみる。
Coyoneda はいわばお布団で、関数と値を隠し持っている。
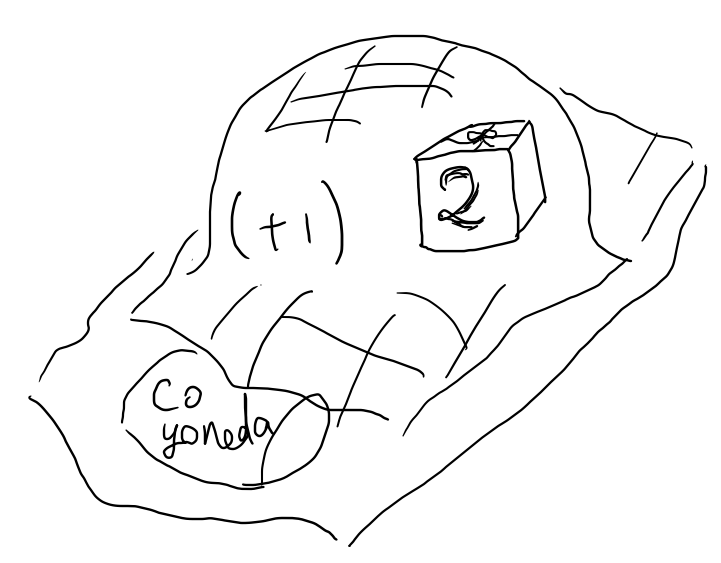
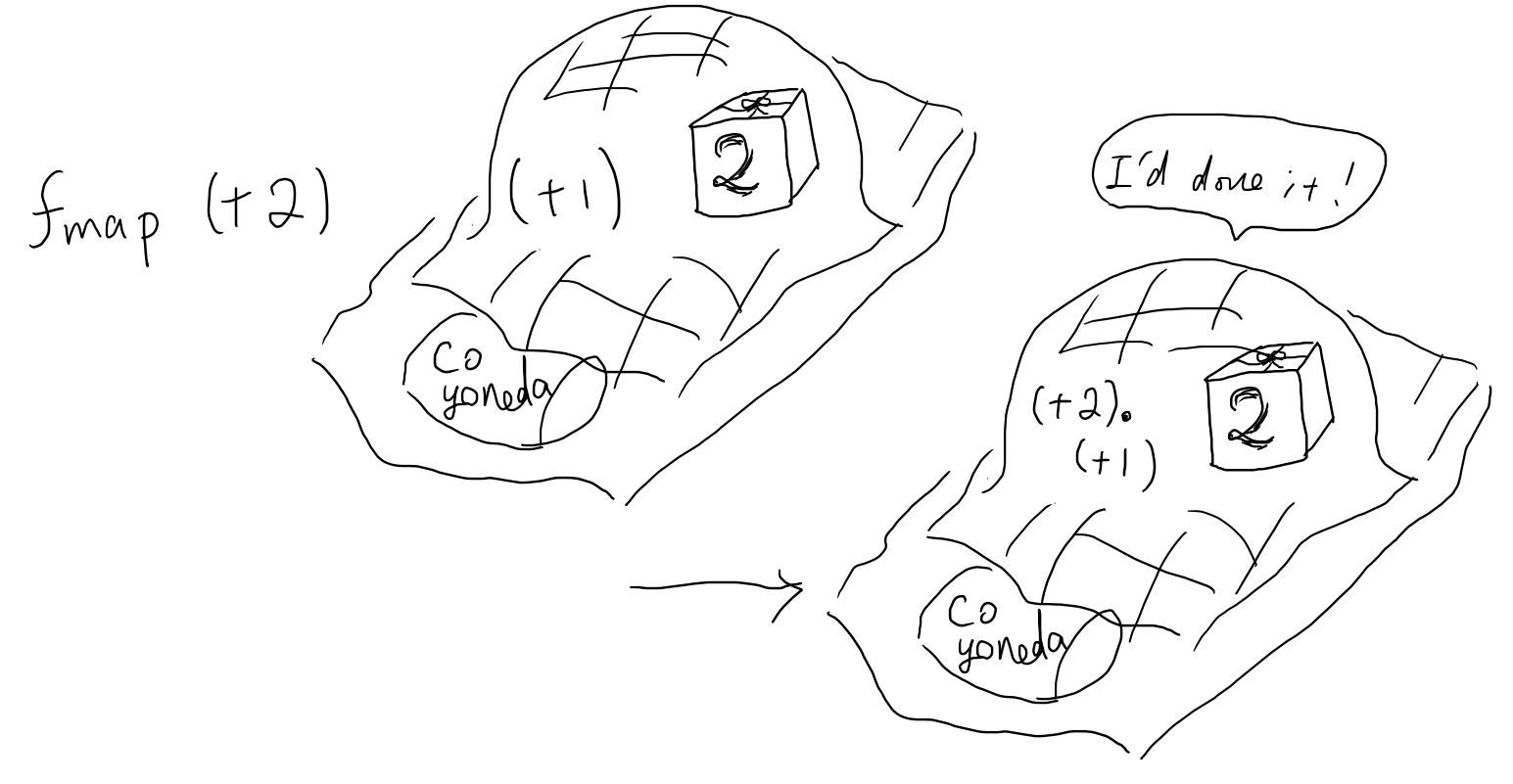
Coyoneda に fmap しても、やったフリをするだけで実際の計算は行わない。
lowerCoyoneda が適用されるとお布団が剥がれ、やっと計算を実行する。
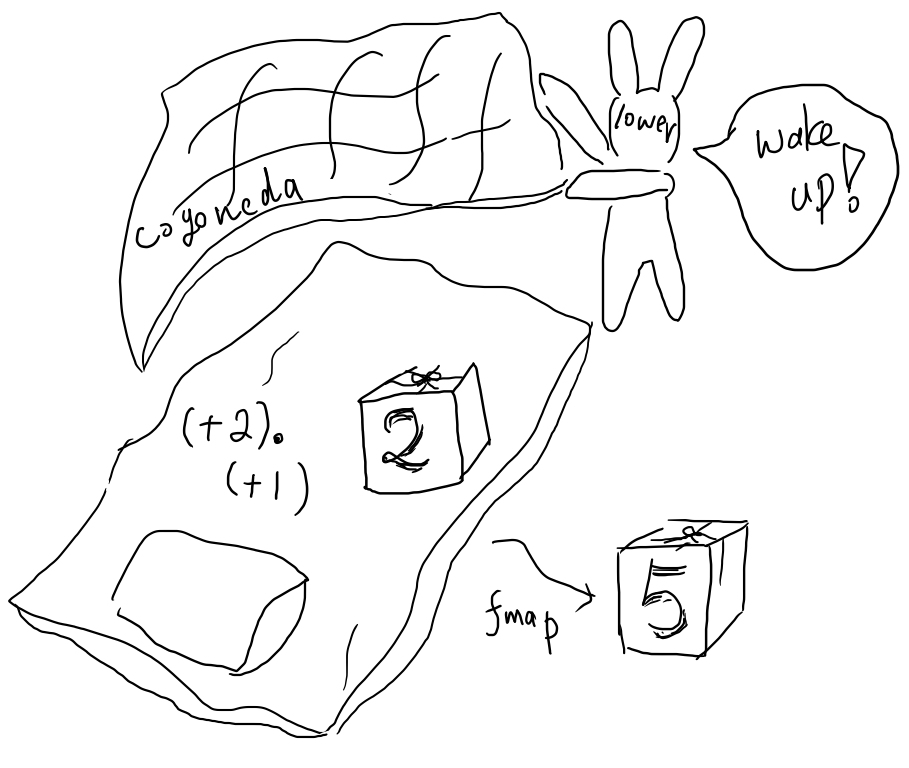
Coyoneda 型においては fmap の適用が自明(trivial)なので、Coyoneda が自由 Functor とでも呼ぶべきものになっているのはこういったわけである。
Yonedaも実現していることは同じである。式がun/currying されているかの違いである。興味深いことに、人間にとっては Coyoneda 形式の方が理解しやすいようである。
参考文献
米田の補題や end, Kan 拡張については次の文献を参考にした。