KaggleにHouse Prices問題でデビュー
はじめに
Kaggleの有名な練習問題であるHouse Prices問題に挑戦してみた。
このコンペでは、アイオワにある住宅の不動産価格をあらゆる説明変数を含むデータセットから予測することが求められている。
今回はランダムフォレストリグレッサーを使って、回帰分析で挑戦してみたいと思う。
なお、今回の分析に使ったコードは、以下のURLにおいてある。
(https://github.com/yzyz2015/HAIT/blob/master/HousePrices_RFR.ipynb)
EDA(Explanatory Data Analysis)
データ数
まずは、train、testデータ数をそれぞれ確認。
# trainデータ
display(train.shape)
# testデータ
display(test.shape)
trainデータの大きさ(1460, 81)
testデータの大きさ(1459, 80)
trainデータはtestデータと同じくらいあり、説明変数はおよそ80個あることがわかる。
次に、変数について見ていきたいと思う。
変数確認
# trainデータの全変数を確認
train.columns
Index(['MSSubClass', 'MSZoning', 'LotFrontage', 'LotArea', 'Street', 'Alley',
'LotShape', 'LandContour', 'Utilities', 'LotConfig', 'LandSlope',
'Neighborhood', 'Condition1', 'Condition2', 'BldgType', 'HouseStyle',
'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd', 'RoofStyle',
'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType', 'MasVnrArea',
'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual', 'BsmtCond',
'BsmtExposure', 'BsmtFinType1', 'BsmtFinSF1', 'BsmtFinType2',
'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', 'Heating', 'HeatingQC',
'CentralAir', 'Electrical', '1stFlrSF', '2ndFlrSF', 'LowQualFinSF',
'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath',
'BedroomAbvGr', 'KitchenAbvGr', 'KitchenQual', 'TotRmsAbvGrd',
'Functional', 'Fireplaces', 'FireplaceQu', 'GarageType', 'GarageYrBlt',
'GarageFinish', 'GarageCars', 'GarageArea', 'GarageQual', 'GarageCond',
'PavedDrive', 'WoodDeckSF', 'OpenPorchSF', 'EnclosedPorch', '3SsnPorch',
'ScreenPorch', 'PoolArea', 'PoolQC', 'Fence', 'MiscFeature', 'MiscVal',
'MoSold', 'YrSold', 'SaleType', 'SaleCondition', 'SalePrice'],
dtype='object')
なお、YearBuiltに関しては時系列に処理し直してもいいのだが予測するうえで特に問題なさそうなのでそのまま分析を進める。
目的変数の分布
## 目的変数の分布
display(train['SalePrice'].describe())
sns.distplot(train['SalePrice']);

正規性に関しては、統計的検定法と仮説検定法を扱わないため今回は特別な処理はせずに分析を進める。
変数ごとの相関
相関行列
# 相関行列でSalePriceと相関が強い説明変数を見つける
corr = train.corr()
plt.figure(figsize=(8,8))
sns.heatmap(corr)
plt.yticks(rotation=0, size=7)
plt.xticks(rotation=90, size=7)
plt.show()
# Select columns with a correlation > 0.5
rel_vars = corr.SalePrice[(corr.SalePrice > 0.5)]
rel_cols = list(rel_vars.index.values)
corr2 = train[rel_cols].corr()
plt.figure(figsize=(8,8))
hm = sns.heatmap(corr2, annot=True, annot_kws={'size':10})
plt.yticks(rotation=0, size=10)
plt.xticks(rotation=90, size=10)
plt.show()

相関行列から、SalePriceに大きな影響を与えるのは以下の10個の説明変数であるとわかった。
・OverallQual: Overall material and finish quality
・YeatBuilt: Original construction date
・YearRemodAdd: Remodel date (same as construction date if no remodeling or additions)
・TotalBsmtSF: Total square feet of basement area
・1stFlrSF: First Floor square feet
・GrLivArea: Above grade (ground) living area square feet
・FullBath: Full bathrooms above grade
・TotRmsAbvGrd: Total rooms above grade (does not include bathrooms)
・GarageCars: Size of garage in car capacity
・GarageArea: Size of garage in square feet
なお、説明変数同士の相関に注目すると、
・1stFlrSFとTotalbsmtSF
・TotRmsAbvGrdとGrLivArea
・GarageAreaとGarageCars
は特に高く、変数の意味を考えてみると多重共線性があるように見え、前処理で工夫する必要がありそうである。
散布図
# SalePriceとの相関が0.5よりも大きい説明変数を選び、散布図を書いてみる
cols_viz = ["OverallQual", "YearBuilt", "YearRemodAdd", "TotalBsmtSF", "1stFlrSF", "GrLivArea", "GarageCars", "GarageArea", "SalePrice"]
sns.pairplot(train[cols_viz], size=2.5)
plt.tight_layout()
plt.show()

相関行列を参考にして、特にSalePriceに影響を与えそうな説明変数を選び、散布図を書いてみた。最右列を確認すればわかる通り、散布図からそれぞれの説明変数とSalePriceの間に正の相関が見て取れる。
欠損値の確認
# 欠損値の数を確認する。
print(train.isnull().sum())
print(test.isnull().sum())
# 欠損値を可視化する。
msno.matrix(df=train, figsize=(20,14), color=(0.5,0,0))
MSSubClass 0
MSZoning 0
LotFrontage 259
LotArea 0
Street 0
Alley 1369
LotShape 0
LandContour 0
Utilities 0
LotConfig 0
LandSlope 0
Neighborhood 0
Condition1 0
Condition2 0
BldgType 0
HouseStyle 0
OverallQual 0
OverallCond 0
YearBuilt 0
YearRemodAdd 0
RoofStyle 0
RoofMatl 0
Exterior1st 0
Exterior2nd 0
MasVnrType 8
MasVnrArea 8
ExterQual 0
ExterCond 0
Foundation 0
BsmtQual 37
...
BedroomAbvGr 0
KitchenAbvGr 0
KitchenQual 0
TotRmsAbvGrd 0
Functional 0
Fireplaces 0
FireplaceQu 690
GarageType 81
GarageYrBlt 81
GarageFinish 81
GarageCars 0
GarageArea 0
GarageQual 81
GarageCond 81
PavedDrive 0
WoodDeckSF 0
OpenPorchSF 0
EnclosedPorch 0
3SsnPorch 0
ScreenPorch 0
PoolArea 0
PoolQC 1453
Fence 1179
MiscFeature 1406
MiscVal 0
MoSold 0
YrSold 0
SaleType 0
SaleCondition 0
SalePrice 0
Length: 80, dtype: int64
MSSubClass 0
MSZoning 4
LotFrontage 227
LotArea 0
Street 0
Alley 1352
LotShape 0
LandContour 0
Utilities 2
LotConfig 0
LandSlope 0
Neighborhood 0
Condition1 0
Condition2 0
BldgType 0
HouseStyle 0
OverallQual 0
OverallCond 0
YearBuilt 0
YearRemodAdd 0
RoofStyle 0
RoofMatl 0
Exterior1st 1
Exterior2nd 1
MasVnrType 16
MasVnrArea 15
ExterQual 0
ExterCond 0
Foundation 0
BsmtQual 44
...
HalfBath 0
BedroomAbvGr 0
KitchenAbvGr 0
KitchenQual 1
TotRmsAbvGrd 0
Functional 2
Fireplaces 0
FireplaceQu 730
GarageType 76
GarageYrBlt 78
GarageFinish 78
GarageCars 1
GarageArea 1
GarageQual 78
GarageCond 78
PavedDrive 0
WoodDeckSF 0
OpenPorchSF 0
EnclosedPorch 0
3SsnPorch 0
ScreenPorch 0
PoolArea 0
PoolQC 1456
Fence 1169
MiscFeature 1408
MiscVal 0
MoSold 0
YrSold 0
SaleType 1
SaleCondition 0
Length: 79, dtype: int64

見たところ、著しく多くの欠損値を持つカラムがいくつかある。先にカラムを処理して、その後で欠損値を多く含む行を個別に処理することにしよう。
前処理
データの可視化をもとに、前処理を行った。
カテゴリデータを数値型データに変換
# trainデータ・testデータともに、カテゴリ型カラムを数値型カラムに変換する
from sklearn.preprocessing import LabelEncoder
for i in range(train.shape[1]):
if train.iloc[:,i].dtypes == object:
lbl = LabelEncoder()
lbl.fit(list(train.iloc[:,i].values) + list(test.iloc[:,i].values))
train.iloc[:,i] = lbl.transform(list(train.iloc[:,i].values))
test.iloc[:,i] = lbl.transform(list(test.iloc[:,i].values))
from sklearn.preprocessing import LabelEncoder
for i in range(test.shape[1]):
if train.iloc[:,i].dtypes == object:
lbl = LabelEncoder()
lbl.fit(list(train.iloc[:,i].values) + list(test.iloc[:,i].values))
train.iloc[:,i] = lbl.transform(list(train.iloc[:,i].values))
test.iloc[:,i] = lbl.transform(list(test.iloc[:,i].values))
カテゴリ型データはそのままでは分析できないので、数値型データに変換した。
変数選択
EDAで確認したように、SalePriceにとって重要な説明変数はそこまで多くなさそうである。ここでは多重共線性を考慮し、相関行列で確認できた説明変数同士の相関を処理したい。
・1stFlrSFとTotalbsmtSFに関しては、1階の広さと地下の広さが相関することを示している。SalePriceとの相関は同じなので、任意で1stFlrSFを採用する。
・TotRmsAbvGrdとGrLivAreaに関しては、地上の部屋のトータル数と地上のリビングの広さが相関することを示している。リビングの広さの方がSalePriceと相関が大きいのでGrLivAreaを採用する。
・GarageAreaとGarageCarsに関しては、ガレージの広さとガレージの車の収容面積が相関することを示している。ガレージの車の収容面積の方がSalePriceとの相関が大きく、ガレージが広ければ車の収容台数が広いのも自然なので、GarageCarsを採用する。
したがって、
・OverallQual
・YeatBuilt
・YearRemodAdd
・1stFlrSF
・GrLivArea
・FullBath
・GarageCars
の7つをモデルに入れる説明変数として採用する。
家全体の質、建築年、広さなど、常識的に考えても不動産価格を決定するのにおかしくない要因であろう。
欠損値の処理
print(train["OverallQual"].isnull().sum())
print(train["YearBuilt"].isnull().sum())
print(train["YearRemodAdd"].isnull().sum())
print(train["1stFlrSF"].isnull().sum())
print(train["GrLivArea"].isnull().sum())
print(train["FullBath"].isnull().sum())
print(train["GarageCars"].isnull().sum())
0
0
0
0
0
0
0
print(test["OverallQual"].isnull().sum())
print(test["YearBuilt"].isnull().sum())
print(test["YearRemodAdd"].isnull().sum())
print(test["1stFlrSF"].isnull().sum())
print(test["GrLivArea"].isnull().sum())
print(test["FullBath"].isnull().sum())
print(test["GarageCars"].isnull().sum())
0
0
0
0
0
0
1
testデータに1つだけ欠損値が見つかったので平均値で補う。
# testデータの欠損値を補完する
test = test['GarageCars'].fillna(test['GarageCars'].mean())
外れ値の処理
外れ値に関しては、SalePriceとそれぞれの説明変数を単回帰の散布図で示し、著しい逸脱があったものは削除した。
OverallQual
# bivariate analysis saleprice/OverallQual
var = 'OverallQual'
data = pd.concat([train['SalePrice'], train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

右の方に外れ値が2点ある。これらを削除する。
# OverallQual
train = train.drop(train[(train['OverallQual']>=10) & (train['SalePrice']<250000)].index)
YearBuilt
# YearBuilt
# bivariate analysis saleprice/YearBuilt
var = "YearBuilt"
data = pd.concat([train['SalePrice'], train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
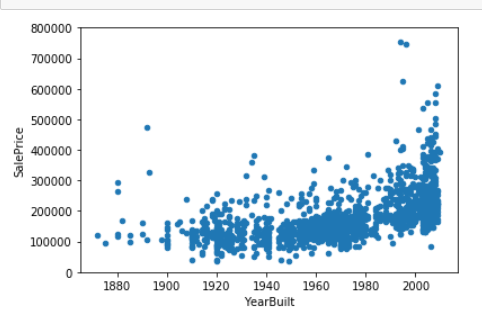
2000年以降に建築されたのに100,000ドル未満の家と1900年頃に建築されたのに400,000ドルより高い家が外れ値に見えるので削除する。
# YearBuilt
train = train.drop(train[(train['YearBuilt']>=2000) & (train['SalePrice']<100000)].index)
train = train.drop(train[(train['YearBuilt']<=1900) & (train['SalePrice']>400000)].index)
YearRemodAdd
# YearRemodAdd
# bivariate analysis saleprice/YearRemodAdd
var = 'YearRemodAdd'
data = pd.concat([train['SalePrice'], train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

1990年以前に改修されたもので350,000ドルより高い家は外れ値に見えるので削除する。
# YearRemodAdd
train = train.drop(train[(train['YearRemodAdd']<=1990) & (train['SalePrice']>350000)].index)
GrLivArea
# GrLivArea
# bivariate analysis saleprice/GrLivArea
var = 'GrLivArea'
data = pd.concat([train['SalePrice'], train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

リビングの広さが3,000より広く、300,000ドルよりも安い家は外れ値に見えるので削除。
# GrLivArea
train = train.drop(train[(train["GrLivArea"]>=3000) & (train['SalePrice']<300000)].index)
本当は説明変数の合成など、細かくやりたいこともあるが時間と労力の都合から今回はこれで前処理を終えて、分析に入りたいと思う。
ランダムフォレスト回帰による学習
今回はランダムフォレスト回帰を使って分析を試みる。
理由としては、EDAで散布図を見たところ線形回帰しているようには見えず、重回帰分析よりも適切であると考えたからである。
加えて、決定木をアンサンブルすることで汎化性能が高く、チューニングするパラメーターが少ないなどのメリットもある。
上記で選定した7つの説明変数でモデルを構築した。
# X,yにデータを代入
X = train.loc[:, ["OverallQual", "YearBuilt", "YearRemodAdd", "1stFlrSF", "GrLivArea", "FullBath", "GarageCars"]].values
y = train["SalePrice"].values
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size= 0.4, random_state=1)
from sklearn.ensemble import RandomForestRegressor
# ランダムフォレスト回帰のクラスをインスタンス化
forest = RandomForestRegressor(n_estimators=100, criterion="mse", random_state=1, n_jobs=-1)
forest.fit(X_train, y_train)
y_train_pred = forest.predict(X_train)
y_test_pred = forest.predict(X_test)
モデルの作成に成功したので、trainデータとtestデータそれぞれのMSEと決定係数を見てみる。
# MSEを出力
from sklearn.metrics import mean_squared_error
print("MSE train: %.3f, test: %.3f" % (mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
# R^2の出力
from sklearn.metrics import r2_score
print("R^2 train: %.3f, test: %.3f" % (r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
MSE train: 137299072.563, test: 1022759699.815
R^2 train: 0.979, test: 0.820
trainデータを見る限り、このモデルは過学習しているようにも見える。とはいえ、testデータの予測値も82%とまずまずの出来であった。
次に、予測された値の残差を見てみる。
# 予測値と残差をプロット
plt.scatter(y_train_pred, y_train_pred - y_train, c = "steelblue", edgecolor = "white", marker ="o", s = 35, alpha = 0.9, label = "training data")
plt.scatter(y_test_pred, y_test_pred - y_test, c = "limegreen", edgecolor = "white", marker = "s", s = 35, alpha = 0.9, label = "test data")

見たところ、trainデータの分布は比較的ランダムで傾向はみられない。testデータの分布は予測された住宅の価格が高いほど散らばりがあるように見える。
本来は残差の分布はランダムであるべきで、そうでないということは、残差の中に価格を説明する要因がまだ残っている可能性がある。さらに分析の精度を上げるには、変数の吟味などやらなければならないことがまだあるようである。
最後に、これをKaggleに提出し、スコアを得ようと思う。
# 作ったモデルをテスト用データに適用してみる
Pred = forest.predict(test.loc[:, ["OverallQual", "YearBuilt", "YearRemodAdd", "1stFlrSF", "GrLivArea", "FullBath", "GarageCars"]].values)
# 提出csvファイルの作成
submit_file = pd.DataFrame({'Id' : test_ID, 'SalePrice' : Pred})
submit_file.to_csv('submit.csv', index = False)
まとめ
Kaggleに提出してみた結果は、スコアが0.17466、ランクは3191/4112と、あまり良くはなかった。
とはいえ、今回は初めてのKaggleへの挑戦で、データ分析のおおよその流れをつかむことはできたと思う。
trainデータから分割したtestデータの予測精度が82%にとどまってしまったのは、特徴量の工夫が足りなかったことによると思う。すべての変数に目を通し、合わせるべきものは合わせたりできれば今回よりも高精度なモデルを作成できるのではないかと思う。
加えて、ランダムフォレストによる特徴量の重要度のランク付けなど、使ってみたいアルゴリズムはまだあったので今後はそうした工夫も付加したい。
今後の展望
今後もKaggleなどに挑戦して成果を確認することはもちろん、機械学習のメソッドがあまり使われることのなかった私の専攻である政治学の領域でも活用していきたい。回帰分析もそうだが、特に政治学の場合はテキストデータが豊富なので、選挙キャンペーンの分析などにおいて自然言語処理を使う機会も多そうである。
加えて、個人的には、院進学で経済系に進むにあたり因果メカニズムを解釈する力も付け、エンジニアリングと理論的な解釈を両方できる人材を目指したい。