はじめに
まずは、ruby や python で「1------------------------1」を計算してみてください。
以下はPythonの例です。
>python
Python 3.7.3 (default, Apr 24 2019, 15:29:51) [MSC v.1915 64 bit (AMD64)] :: Anaconda, Inc. on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> 1------------------------1
2
>>>
一見エラーとなりそうなコーディングですが、エラーとなりませんね。
さて、どうしてでしょうか?
マイナス記号(-)には3つの意味がある。
実はマイナス記号は次の3つの意味を持っています。
1.負数を表す「符号」としてのマイナス記号
これは一番ポピュラーですね。つまり、「-1」「-2」「-100」とか、負の数字を表す符号としてのマイナスです。
厳密にいうと、負符号のマイナス記号は単項演算子なのですが、わかりにくいので符号ということにしましょう。
2.「単項演算子」としてのマイナス記号
これは、例えば「-a」「-(b+c)」のマイナスです。
意味としては、直後の数字(aやb+c)の符号を逆転する(負なら正、正なら負)にする、となりますね。
3.「二項演算子」としてのマイナス記号
これは「a-b」のマイナスですね。aからbを引くという意味ですね。
以上をもとに順にひも解いていってみましょう。
(1) 1--1
この式は 1-(-1) と解釈されます。
つまり、最初のマイナス記号は「二項演算子」で、2つ目のマイナス記号は「符号」ですね。計算結果は2になりますね。
(2) 1---1
この式は、1-(-(-1)) と解釈されます。
すなわち、1つ目のマイナス記号が「二項演算子」、2つ目のマイナス記号が「単項演算子」、3つ目のマイナス記号が「符号」です。
計算結果は0ですね。
(3) 1----1
この式は、1-(-(-(-1))) と解釈されます。
最初が「二項演算子」、最後が「符号」、中の2つが「単項演算子」ですね。計算結果は2です。
つまり、1と1の間に、マイナスがn個あるとすると、1番目のマイナス記号は「二項演算子」、最後(n個目)のマイナス記号は「符号」、そして、中の(n-2)個のマイナス記号は「単項演算子」と見なされるわけです。
また、計算結果は、nが偶数のときは2、奇数のときは0になることは数学的帰納法で証明できますね。
最後に
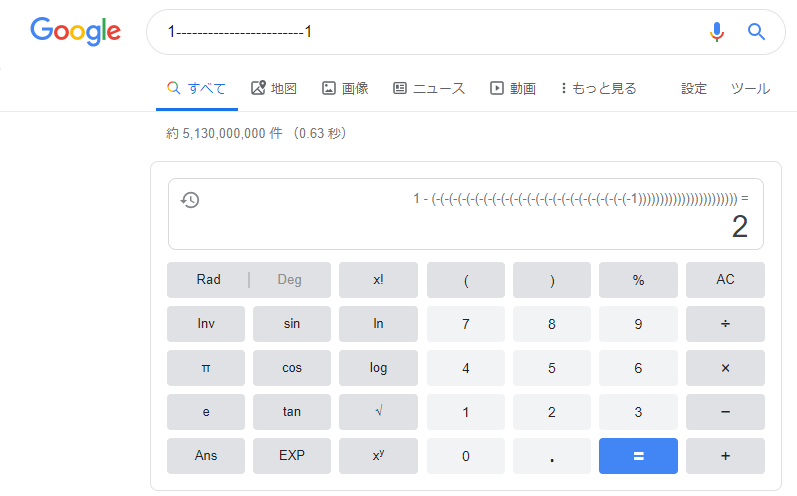
参考まで、グーグル検索窓に「1------------------------1」を入れてみたら下記のようになりました。
計算過程まで表示してくれるので、なぜ2になるのかがよくわかりますね。