PCL(Point Cloud Library)の勉強にあたって、公式サイトのチュートリアルの紹介をしたいと思います。間違いやおかしな点あればご指摘ください。
各項の詳細なチュートリアルも随時更新していこうと思います!
PCL概要
初めに、チュートリアルを見ていく前に概要について触れたいと思います!
PCLは大規模な3D点群オープンプロジェクトであり、フィルタリング、特徴推定、サーフェス再構成、レジストレーション(位置合わせ)、モデルフィッティング、セグメンテーションなど、たくさんの最先端のアルゴリズムが含まれています。
Kinectセンサの登場によって誰でも点群(point cloud)がリアルタイムに取得できるようになり、その3次元点群に対して処理を行うことができるライブラリがPCLということで注目を集めています。
VTKやOpenNIとの連携も可能で、3D表示はVTKで行うことができ、KinectのデータをOpenNIで取得することができます。
1. Features
・k-NN, 法線推定など
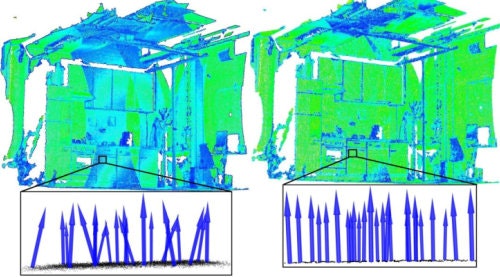
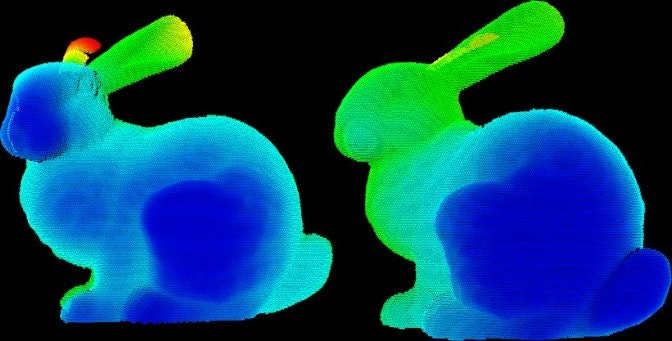
Featureライブラリは、点群データから3次元特徴推定のためのデータ構造とメカニズムが含まれています(特徴点探索については 3. KeyPoints で述べられています)。これらは主に法線(normals)の推定をする際に用いられます。法線方向の情報は、光の反射などの視覚効果を作成する上で重要な情報となります。
3次元特徴は、ある点の周囲から得られる情報に基づいた幾何学的なパターンによって描画される点群や空間で表現されます。クエリ点の周りの選択されたデータ空間はk近傍(k-neighborhood)と呼びます。近傍を効率的に求めるために、PCLではoctreeあるいはkD-treeのような空間分割テクニックを用いて小さな塊に分割し、その中で最近傍探索が行われます。
点群からの法線推定は、「最小二乗法 (least-squares)により、局所的な点群(k近傍)に対して平面を当てはめることで、その平面をサーフェスとみなし、サーフェスの垂直方向を法線とする。」というように求めることができます。
Documentation: http://docs.pointclouds.org/trunk/group__features.html
Tutorials: http://pointclouds.org/documentation/tutorials/#features-tutorial
2. Filter
・ノイズ除, ダウンサンプリングなど
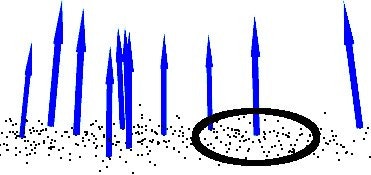
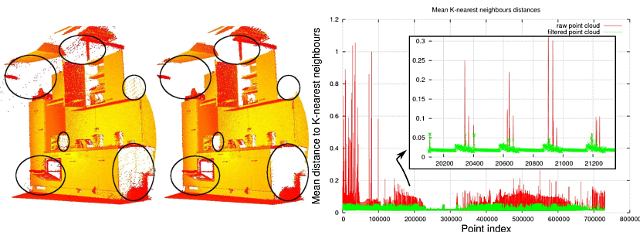
計測誤差によって、いくつかのデータにはノイズが発生します。これによって局所的な点群の3次元特徴を推定するのが困難になることがあります。
これらの外れ値(outlier)の一部は、各点の近傍に統計分析を行い、一定の基準を満たしていないものをトリミングすることによって除外することができます。 PCLでのスパース外れ値除去の実装は、入力データセット内の点の隣接距離の分布の計算に基づいています。
Documentation: http://docs.pointclouds.org/trunk/group__filters.html
Tutorials: http://pointclouds.org/documentation/tutorials/#filtering-tutorial
3. I/O
・ファイル入出力
I/Oライブラリでは、PCD(point cloud data)ファイルの読み書きだけでなく、様々なセンシングデバイスからの点群の取得に関するクラスや関数を含んでいます。OpenNIと連携しているため、Kinectのデータを取得することもできます。
Documentation: http://docs.pointclouds.org/1.7.2/a02409.html
Tutorials: http://pointclouds.org/documentation/tutorials/#i-o
4. Keypoints
・特徴点探索(AGAST, BRISK, Harris, NARF, SIFTなど)
Keypointsライブラリでは、特徴点探索アルゴリズムが含まれています。特徴点とは、画像や点群における、不変で独特であり、定義された判断基準を用いて区別可能な点を意味します。
PCLに限らず、コンピュータビジョンでの画像および3Dでの特徴量を用いた計算は、以下の3段階で順に行われます。
①Keypointの検出(pcl::keypoints)
②KeypointでのDescriptorの計算(pcl::features)
③Descriptor同士での対応計算(pcl::search, pcl::kdtree)
Documentation: http://docs.pointclouds.org/trunk/group__keypoints.html
Tutorials: http://pointclouds.org/documentation/tutorials/#keypoints-tutorial
5. KdTree
・最近傍探索、ダウンサンプリングなど
PCLのKdTreeモジュールは、FLANNというライブラリを採用しており、高速に最近傍探索が可能です。後述するOctreeもそうですが、「3D空間を効率的に分割しておき、高速な探索を行うための仕組み」です。
例えば、1万点から構成される3D点群データ内で、ある注目点の10個の近傍点を探したいという時にkdtree無しに全探索しようとすると1万点全てとの注目点の距離を計算することになりますが、kdtreeを用いると、バイナリーサーチとなるので、効率よく探索範囲を絞っていくことで、少ない計算コストで近傍探索を行う事ができます。
Documentation: http://docs.pointclouds.org/1.7.2/a02410.html
Tutorials: http://pointclouds.org/documentation/tutorials/#kdtree-tutorial
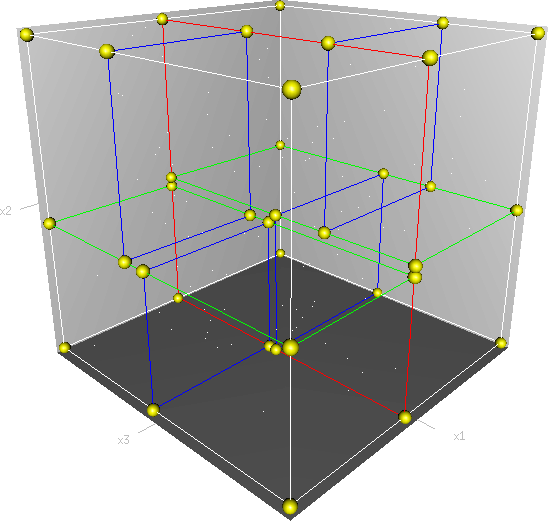
以下は3次元のkd木であり、根セル(白)をまず2つの部分セルに分割(赤)し、それぞれをさらに2つに分割(緑)しています。最後に4つのセルそれぞれを2つに分割(青)しています。それ以上の分割はされていないので、最終的にできた8つのセルを葉セルと呼びます。黄色の球は木の頂点を表しています。
6. Octree
・最近傍探索、ダウンサンプリングなど
Octreeモジュールはkd-tree同様、点群データから効率的に階層的木構造を作成するために用いられます。CG業界でもよく用いられ、対象の3Dデータを探索したり処理するために効率的な構造を八分木により作っておくという空間分割によるデータ構造です。
Octreeは3次元空間中のオブジェクト(点群)を、そのデータの配置具合にそって適応的に空間分割してくれるので,各ノード(立方体)ごとに点の密度を計算したり,kdtreeのように木構造を使って八分木探索したり,グリッドごとに占有度(Occupancy)管理も可能というわけです。
Documentation: http://docs.pointclouds.org/1.7.2/a02412.html
Tutorials: http://pointclouds.org/documentation/tutorials/#octree-tutorial
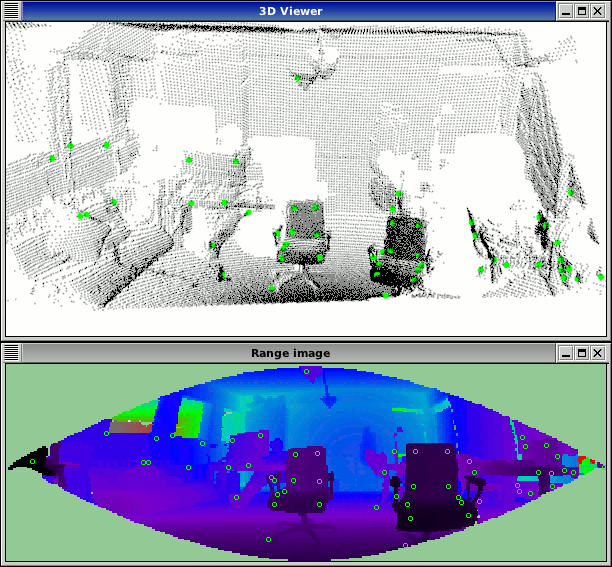
7. Range Images
各画素値の値がセンサーからの距離あるいは深度を表現する画像をRange image あるいはDepth map といいます。
カメラの内部パラメータがわかっていれば、range image は点群に落とし込むことができます。
Tutorials: http://pointclouds.org/documentation/tutorials/#range-images
8. Recognition
・物体認識
Recognitionモジュールでは、物体認識アプリケーションのためのアルゴリズムが含まれています。ただ、その種類自体はそれほど多くないかなといった印象です。RANSACベースの認識などがあります。
Documentation: http://docs.pointclouds.org/1.7.2/a02414.html
Tutorials: http://pointclouds.org/documentation/tutorials/#recognition-tutorial
9. Registration
・レジストレーション
いくつかのローカルなデータセットをグローバルな一貫したモデルに結合するためのテクニックは、レジストレーション(registration)と呼ばれます。これは、データセット間の対応する点を特定(pcl::keypoint, pcl::features)し、対応点間の距離(alignment error)が最小になるような変換を推定する方法です。対応点探索はデータセットの姿勢や方向に影響を受けるため、繰り返し計算を行います。対応点間の距離がある閾値以下になったらレジストレーション処理は終了です。
Documentation: http://docs.pointclouds.org/trunk/group__registration.html
Tutorials: http://pointclouds.org/documentation/tutorials/#registration-tutorial
10. Sample Consensus
・物体検出、セグメンテーションなど
RANSACのような手法で、平面や円筒の検出に用いられます。平面のフィッティングは、壁や床、テーブルなどのサーフェスの検出タスクによく用いられます。
Documentation: http://docs.pointclouds.org/1.7.2/a02416.html
Tutorials: http://pointclouds.org/documentation/tutorials/#sample-consensus
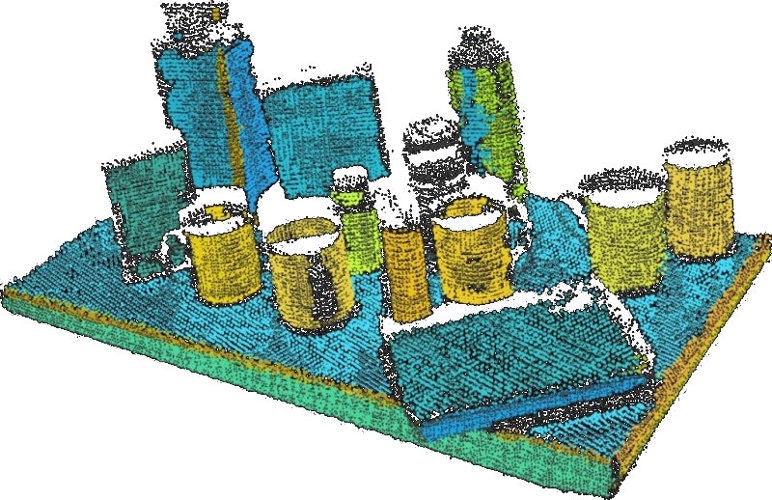
11. Segmentation
・セグメンテーション
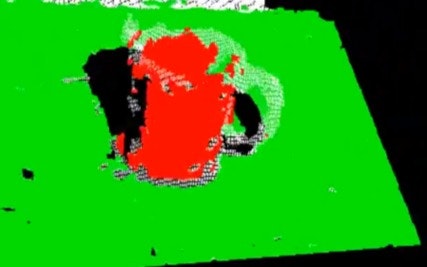
PCLのSegmentationモジュールは区別可能なクラスタにまとめるアルゴリズムを含んでいます。これらのアルゴリズムは、たくさんの空間的に独立した領域から構成される点群を処理するのに適しています。クラスタリングなどを用いて、点群を複数のかたまりに自動的に分離することができます。しかしながら、画像のときのようなきれいなセグメンテーションは難しいようです。
Documentation: http://docs.pointclouds.org/1.7.2/a02418.html
Tutorials: http://pointclouds.org/documentation/tutorials/#segmentation-tutorial
12. Surface
Surfaceモジュールでは、メッシュの生成、平滑化、リサンプリングなどが含まれています。平滑化やリサンプリングは点群がノイジーなときや完全に整合されていないマルチスキャンから構成されるものを処理する場合にはとても重要です。
メッシングは点群の周りにサーフェスを作る一般的な方法です。
convex hull あるいは concave hull は、例えば単純なサーフェスの形状を知りたいときや境界を知りたいときに有効です。
Documentation: http://docs.pointclouds.org/1.7.2/a02419.html
Tutorials: http://pointclouds.org/documentation/tutorials/#surface-tutorial
13. Visualization
・可視化
Visualizationモジュールでは、点群やアルゴリズムの結果の3D可視化を行うことができます。
OpenCVでいうところのhighguiのようなものです。
Documentation: http://docs.pointclouds.org/1.7.2/a02420.html
Tutorials: http://pointclouds.org/documentation/tutorials/#visualization-tutorial