Unityでスライムを作ろう！

この記事は Akatsuki Advent Calendar 2021 14日目の記事です。
13日目は、アディさんの「カードゲームクリエイターで快適ポケカライフを過ごす」でした。

はじめに

はじめまして、新卒クライアントエンジニアのyuyuです。
アカツキにはハイパーカジュアルゲームを作る研修があるのですが、そこで作ったゲームにスライムの表現を入れました（下の画像参照）。
それが思いの外いい感じになったので、記事として残すことにしました。

本記事では、全体の工程を10ステップに分割して説明していきます。
最終的にはこのような画を作っていきます。

プロジェクトはこちらにアップしています。

対象の読者

この記事は、以下のような方を対象としています。

• シェーダーやレイマーチングの経験があり、スライム的な表現のミソを知りたい
• シェーダーやレイマーチングの経験はないが、実際に動くコードや途中経過を見られれば嬉しい

レイマーチングそのものについては解説をしていないので、気になる方は調べていただければと思います。

本編

それでは本編です。レッツスライム。

Step0 準備

まずは、ベースとなるシェーダーを用意します。
Unityでシェーダーを作成すると初期状態でウワ〜〜っと書かれていますが、今回は必要な部分を抜き出したり追加したりしたものを使います。

追加ポイントとしてはこんな感じ。

• 透過できる（透明度が有効になる）ように
• 深度を書き込むように
• ピクセルのワールド座標が使えるように

step0.shader

Shader "Slime/Step0"
{
    Properties {}
    SubShader
    {
        Tags
        {
            "Queue" = "Transparent" // 透過できるようにする
        }

        Pass
        {
            ZWrite On // 深度を書き込む
            Blend SrcAlpha OneMinusSrcAlpha // 透過できるようにする

            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            // 入力データ用の構造体
            struct input
            {
                float4 vertex : POSITION; // 頂点座標
            };

            // vertで計算してfragに渡す用の構造体
            struct v2f
            {
                float4 pos : POSITION1; // ピクセルワールド座標
                float4 vertex : SV_POSITION; // 頂点座標
            };

            // 出力データ用の構造体
            struct output
            {
                float4 col: SV_Target; // ピクセル色
                float depth : SV_Depth; // 深度
            };

            // 入力 -> v2f
            v2f vert(const input v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.pos = mul(unity_ObjectToWorld, v.vertex); // ローカル座標をワールド座標に変換
                return o;
            }

            // v2f -> 出力
            output frag(const v2f i)
            {
                output o;
                o.col = fixed4(i.pos.xyz, 0.5);
                o.depth = 1;
                return o;
            }
            ENDCG
        }
    }
}

そして、このシェーダーを設定したマテリアルと、マテリアルを適用させた平面を作ります。
平面はカメラの画角を覆うように配置しておきましょう。

色は平面の座標で変わってきますが、このような見た目になります（既にスライムっぽい）。

Step1 レイマーチングで球を表示する

それでは、基本となる球をレイマーチングを使って表示していきましょう。

今回使う球の距離関数は、渡したfloat4型の引数のxyz成分で球の中心座標を、w成分で半径を表すような仕様にしました。

とりあえず、座標(0, 0, 0)に半径0.5の球を表示させるシェーダーがこんな感じです。

Step1.shader

Shader "Slime/Step1"
{
    Properties {}
    SubShader
    {
        Tags
        {
            "Queue" = "Transparent" // 透過できるようにする
        }

        Pass
        {
            ZWrite On // 深度を書き込む
            Blend SrcAlpha OneMinusSrcAlpha // 透過できるようにする

            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            // 入力データ用の構造体
            struct input
            {
                float4 vertex : POSITION; // 頂点座標
            };

            // vertで計算してfragに渡す用の構造体
            struct v2f
            {
                float4 pos : POSITION1; // ピクセルワールド座標
                float4 vertex : SV_POSITION; // 頂点座標
            };

            // 出力データ用の構造体
            struct output
            {
                float4 col: SV_Target; // ピクセル色
                float depth : SV_Depth; // 深度
            };

            // 入力 -> v2f
            v2f vert(const input v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.pos = mul(unity_ObjectToWorld, v.vertex); // ローカル座標をワールド座標に変換
                return o;
            }

+           // 球の距離関数
+           float4 sphereDistanceFunction(float4 sphere, float3 pos)
+           {
+               return length(sphere.xyz - pos) - sphere.w;
+           }

+           // 深度計算
+           inline float getDepth(float3 pos)
+           {
+               const float4 vpPos = mul(UNITY_MATRIX_VP, float4(pos, 1.0));
+               
+               float z = vpPos.z / vpPos.w;
+               #if defined(SHADER_API_GLCORE) || \
+                   defined(SHADER_API_OPENGL) || \
+                   defined(SHADER_API_GLES) || \
+                   defined(SHADER_API_GLES3)
+               return z * 0.5 + 0.5;
+               #else
+               return z;
+               #endif
+           }

            // v2f -> 出力
            output frag(const v2f i)
            {
                output o;

+               float3 pos = i.pos.xyz; // レイの座標（ピクセルのワールド座標で初期化）
+               const float3 rayDir = normalize(pos.xyz - _WorldSpaceCameraPos); // レイの進行方向
+
+               float4 sphere = float4(0, 0, 0, 0.5); // 球の座標と半径
+               
+               for (int i = 0; i < 30; i++)
+               {
+                   // posと球との最短距離
+                   float dist = sphereDistanceFunction(sphere, pos);
+
+                   // 距離が0.001以下になったら、色と深度を書き込んで処理終了
+                   if (dist < 0.001)
+                   {
+                       o.col = fixed4(0, 1, 0, 0.5); // 塗りつぶし
+                       o.depth = getDepth(pos); // 深度書き込み
+                       return o;
+                   }
+
+                   // レイの方向に行進
+                   pos += dist * rayDir;
+               }
+
+               // 衝突判定がなかったら透明にする
+               o.col = 0;
+               o.depth = 0;
+               return o;
            }
            ENDCG
        }
    }
}

ループ回数の30はステップ数です。レイマーチングでは、文字通りレイを行進させて物体との衝突を確認していくわけですが、最大何回レイを行進させるかというのがこの数字になります。
また、条件式内の0.001という数字は閾値で、レイの位置と球の表面との距離がこの値未満になったときにピクセルを塗りつぶします。
（ワールド座標から深度情報への変換はこちらのページを参考にしています）

これで、指定した座標に球らしきものが表示されるようになりました。

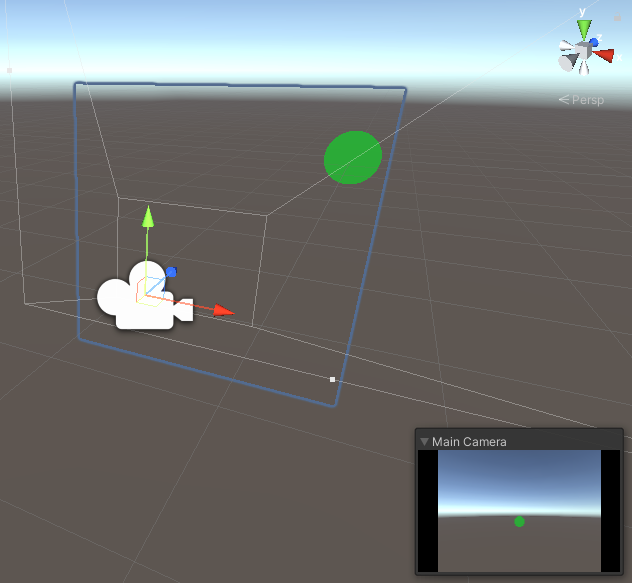
試しに球と重なるようにPlaneを設置すると、ちゃんと球の一部分が欠けています。深度も正しく反映されているようです。

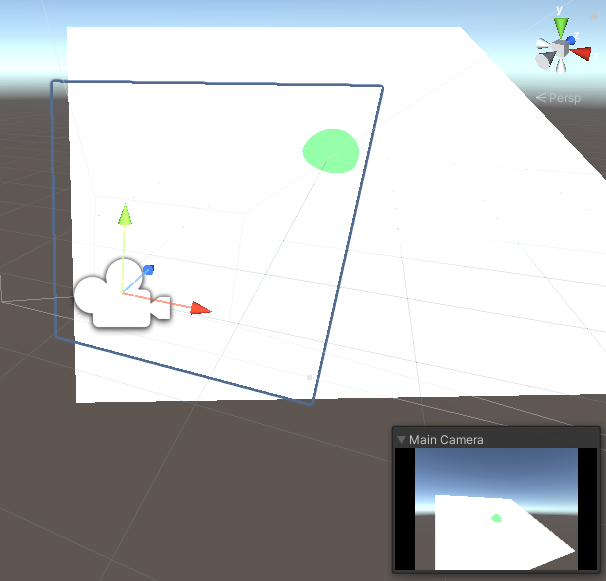
Step2 球をたくさん表示する

Step1では1つだけでしたが、複数の球が表示できるように拡張していきます。
レイマーチングでは、距離関数のminをとることで、レイが複数ある球のどれかに衝突したピクセルを塗りつぶすことができます。

球の座標と半径を配列に格納し、距離関数をループさせてminをとる getDistance を追加しました。
（一旦座標と半径をランダムに設定するために余計なコードが何行か追加されていますが、次のステップで削除します）

Step2.shader

Shader "Slime/Step2"
{
    Properties {}
    SubShader
    {
        Tags
        {
            "Queue" = "Transparent" // 透過できるようにする
        }

        Pass
        {
            ZWrite On // 深度を書き込む
            Blend SrcAlpha OneMinusSrcAlpha // 透過できるようにする

            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            // 入力データ用の構造体
            struct input
            {
                float4 vertex : POSITION; // 頂点座標
            };

            // vertで計算してfragに渡す用の構造体
            struct v2f
            {
                float4 pos : POSITION1; // ピクセルワールド座標
                float4 vertex : SV_POSITION; // 頂点座標
            };

            // 出力データ用の構造体
            struct output
            {
                float4 col: SV_Target; // ピクセル色
                float depth : SV_Depth; // 深度
            };

            // 入力 -> v2f
            v2f vert(const input v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.pos = mul(unity_ObjectToWorld, v.vertex); // ローカル座標をワールド座標に変換
                return o;
            }

            // 球の距離関数
            float4 sphereDistanceFunction(float4 sphere, float3 pos)
            {
                return length(sphere.xyz - pos) - sphere.w;
            }

            // 深度計算
            inline float getDepth(float3 pos)
            {
                const float4 vpPos = mul(UNITY_MATRIX_VP, float4(pos, 1.0));

                float z = vpPos.z / vpPos.w;
                #if defined(SHADER_API_GLCORE) || \
                    defined(SHADER_API_OPENGL) || \
                    defined(SHADER_API_GLES) || \
                    defined(SHADER_API_GLES3)
                return z * 0.5 + 0.5;
                #else
                return z;
                #endif
            }

+           #define MAX_SPHERE_COUNT 256 // 最大の球の個数
+           float4 _Spheres[MAX_SPHERE_COUNT]; // 球の座標・半径を格納した配列
+           int _SphereCount; // 処理する球の個数

+           // いずれかの球との最短距離を返す
+           float getDistance(float3 pos)
+           {
+               float dist = 100000;
+               for (int i = 0; i < _SphereCount; i++)
+               {
+                   dist = min(dist, sphereDistanceFunction(_Spheres[i], pos));
+               }
+               return dist;
+           }

+           // ランダムな値を返す（後で削除）
+           float rand(float2 seed)
+           {
+               return frac(sin(dot(seed.xy, float2(12.9898, 78.233))) * 43758.5453);
+           }

            // v2f -> 出力
            output frag(const v2f i)
            {
                output o;

                float3 pos = i.pos.xyz; // レイの座標（ピクセルのワールド座標で初期化）
                const float3 rayDir = normalize(pos.xyz - _WorldSpaceCameraPos); // レイの進行方向

+               // 球の座標と半径をランダムに設定（後で削除）
+               _SphereCount = 256;
+               for (int x = 0; x < _SphereCount; x++)
+               {
+                   float3 center = float3(rand(x), rand(x + 1), rand(x + 2)) * 8 - 4;
+                   float radius = rand(x + 3) * .5;
+                   _Spheres[x] = float4(center, radius);
+               }

                for (int i = 0; i < 30; i++)
                {
+                   // posといずれかの球との最短距離
+                   float dist = getDistance(pos);

                    // 距離が0.001以下になったら、色と深度を書き込んで処理終了
                    if (dist < 0.001)
                    {
                        o.col = fixed4(0, 1, 0, 0.5); // 塗りつぶし
                        o.depth = getDepth(pos); // 深度書き込み
                        return o;
                    }

                    // レイの方向に行進
                    pos += dist * rayDir;
                }

                // 衝突判定がなかったら透明にする
                o.col = 0;
                o.depth = 0;
                return o;
            }
            ENDCG
        }
    }
}

ロボットアニメで敵機を一気に倒した時のアレみたいになってきたぞ。

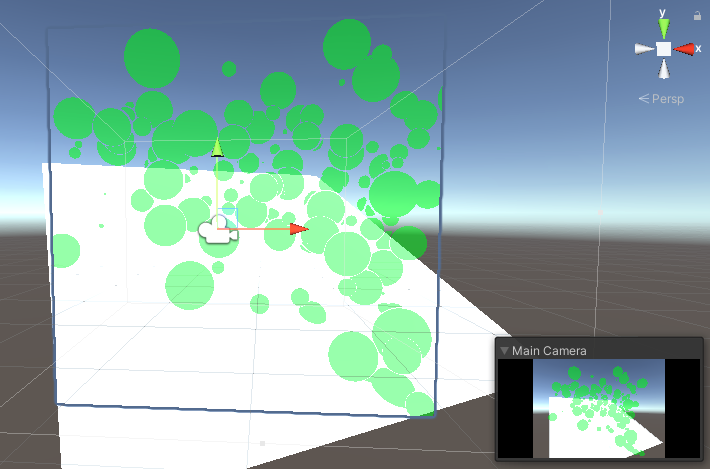
Step3 球の座標・半径をColliderとリンクさせる

Step2ではランダムだった球の座標と半径を、シーン内のColliderの情報をもとに設定していきます。

まず、シェーダー側から不要なコードを削除します。

Step3.shader（一部抜粋）

// 全ての球との最短距離を返す
float getDistance(float3 pos)
{
    float dist = 100000;
    for (int i = 0; i < _SphereCount; i++)
    {
        dist = min(dist, sphereDistanceFunction(_Spheres[i], pos));
    }
    return dist;
}

-// ランダムな値を返す
-float rand(float2 seed)
-{
-   return frac(sin(dot(seed.xy, float2(12.9898, 78.233))) * 43758.5453);
-}

// v2f -> 出力
output frag(const v2f i)
{
    output o;

    float3 pos = i.pos.xyz; // レイの座標（ピクセルのワールド座標で初期化）
    const float3 rayDir = normalize(pos.xyz - _WorldSpaceCameraPos); // レイの進行方向

-   _SphereCount = 256;
-   for (int x = 0; x < _SphereCount; x++)
-   {
-       float3 center = float3(rand(x), rand(x + 1), rand(x + 2)) * 8 - 4;
-       float radius = rand(x + 3) * .5;
-       _Spheres[x] = float4(center, radius);
-   }

    for (int i = 0; i < 30; i++)
    {
        // posと球との最短距離
        float dist = getDistance(pos);

        // 距離が0.001以下になったら、色と深度を書き込んで処理終了
        if (dist < 0.001)
        {
            o.col = fixed4(0, 1, 0, 0.5); // 塗りつぶし
            o.depth = getDepth(pos); // 深度書き込み
            return o;
        }

        // レイの方向に行進
        pos += dist * rayDir;
    }

    // 衝突判定がなかったら透明にする
    o.col = 0;
    o.depth = 0;
    return o;
}

そして、_Spheres、_SphereCount を、シーンに設置したColliderに合わせて設定するスクリプトを作成します。名前は SlimeRenderer としました。

SlimeRenderer.cs

using UnityEngine;

[ExecuteAlways] // 再生していない間も座標と半径が変化するように
public class SlimeRenderer : MonoBehaviour
{
    [SerializeField] private Material material; // スライム用のマテリアル

    private const int MaxSphereCount = 256; // 球の最大個数（シェーダー側と合わせる）
    private readonly Vector4[] _spheres = new Vector4[MaxSphereCount];
    private SphereCollider[] _colliders;

    private void Start()
    {
        // 子のSphereColliderをすべて取得
        _colliders = GetComponentsInChildren<SphereCollider>();

        // シェーダー側の _SphereCount を更新
        material.SetInt("_SphereCount", _colliders.Length);
    }

    private void Update()
    {
        // 子のSphereColliderの分だけ、_spheres に中心座標と半径を入れていく
        for (var i = 0; i < _colliders.Length; i++)
        {
            var col = _colliders[i];
            var t = col.transform;
            var center = t.position;
            var radius = t.lossyScale.x * col.radius;
            // 中心座標と半径を格納
            _spheres[i] = new Vector4(center.x, center.y, center.z, radius);
        }

        // シェーダー側の _Spheres を更新
        material.SetVectorArray("_Spheres", _spheres);
    }
}

SetVectorArray は引数にプロパティ名とVector4型の配列をとります。
今回はちょうど、球を4つの成分（xyz=座標、w=半径）で表現していたので、そのようなVector4型の値を格納した配列を作って、マテリアルに渡しています。

さらに、SlimeRendererをアタッチしたゲームオブジェクトの子として、RigidbodyとColliderを付けた球をたくさん設置します。

シーンを再生すると、緑色の球体が描画されました。

MeshRendererによる描画と重複してしまっていたので、MeshRendererを無効にしておきます。

Step4 球を滑らかに繋げる

さて、今回のキーポイントです。複数の球を滑らかに繋げて、スライム感を出していきます。
レイマーチングでこれを行うときは、距離関数同士のminをとるときに、単純な大小比較ではなくある特殊な関数（smooth min関数）を使います。
smooth min関数には色々な種類があるのですが、今回は対数と指数を使った以下の関数 $m_s$ を使うことにします（こちらのページを参考にしました）。
$$ m_s\left(x_{1},x_{2}\right)=-\frac{1}{k}\log\left(\exp\left(-kx_{1}\right)+\exp\left(-kx_{2}\right)\right) $$
ここで、$x_1$, $x_2$ はminをとる対象です。また $k$ は定数で、$k$ が小さいほど滑らかになり、$k$ が大きいほど通常のminに近づきます。
下のグラフは青の点線と緑の点線をminをとる対象とし、$k=4,10,50$ でこの関数の値をプロットしたものです。

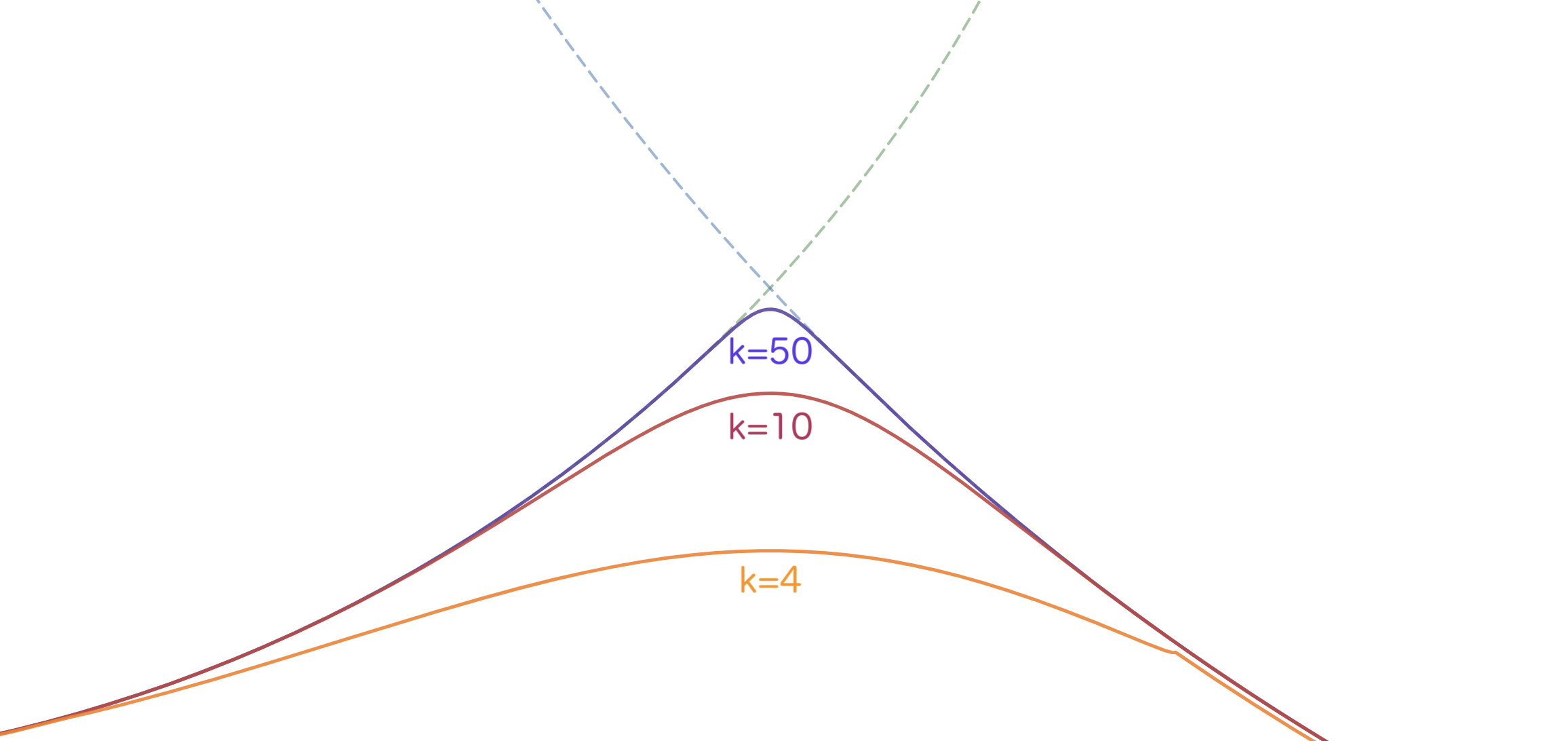
シェーダーのコードに落とし込むとこうなります。

Step4.shader（一部抜粋）

+// smooth min関数
+float smoothMin(float x1, float x2, float k)
+{
+   return -log(exp(-k * x1) + exp(-k * x2)) / k;
+}

// 全ての球との最短距離を返す
float getDistance(float3 pos)
{
    float dist = 100000;
    for (int i = 0; i < _SphereCount; i++)
    {
-       dist = min(dist, sphereDistanceFunction(_Spheres[i], pos));
+       dist = smoothMin(dist, sphereDistanceFunction(_Spheres[i], pos), 3);
    }
    return dist;
}

再生するとこうなりました。

球の端が一部透明になってしまっていますね。これは描画の対象となる形状の面がレイと平行に近いときに発生します。滑らかに繋げたことによってそのような面が増えてしまったようです。
解消するには、レイマーチングのステップ数を上げるか（副作用として動作が重くなります）、塗りつぶしの閾値を上げます（副作用として深度や法線の品質が下がります）。
ステップ数を30から40に、閾値を0.001から0.01に上げると、以下のようになりました。

ちなみに、このように複数の球を滑らかに繋げたものを「メタボール」と呼んだりします。

Step5 色をつける

緑一色（リューイーソーではない）でもいいのですが、せっかくなのでカラフルにしてみます。

こちらのページを参考に、色が滑らかに変化していくような実装をします。

まず、シェーダーにコードを追加します。getColor メソッドを追加し、この結果をもとにピクセルの塗りつぶし色を変えるようにします。

Step5.shader（一部抜粋）

+fixed3 _Colors[MAX_SPHERE_COUNT]; // 球の色を格納した配列

+fixed3 getColor(const float3 pos)
+{
+   fixed3 color = fixed3(0, 0, 0);
+   float weight = 0.01;
+   for (int i = 0; i < _SphereCount; i++)
+   {
+       const float distinctness = 0.7;
+       const float4 sphere = _Spheres[i];
+       const float x = clamp((length(sphere.xyz - pos) - sphere.w) * distinctness, 0, 1);
+       const float t = 1.0 - x * x * (3.0 - 2.0 * x);
+       color += t * _Colors[i];
+       weight += t;
+   }
+   color /= weight;
+   return float4(color, 1);
+}

// v2f -> 出力
output frag(const v2f i)
{
    output o;

    float3 pos = i.pos.xyz; // レイの座標（ピクセルのワールド座標で初期化）
    const float3 rayDir = normalize(pos.xyz - _WorldSpaceCameraPos); // レイの進行方向

    for (int i = 0; i < 40; i++)
    {
        // posと球との最短距離
        float dist = getDistance(pos);

        // 距離が0.01以下になったら、色と深度を書き込んで処理終了
        if (dist < 0.01)
        {
-           o.col = fixed4(0, 1, 0, 0.5); // 塗りつぶし
+           fixed3 color = getColor(pos); // 色
+           o.col = fixed4(color, 1); // 塗りつぶし
            o.depth = getDepth(pos); // 深度書き込み
            return o;
        }

        // レイの方向に行進
        pos += dist * rayDir;
    }

    // 衝突判定がなかったら透明にする
    o.col = 0;
    o.depth = 0;
    return o;
}

getColor メソッド中の distinctness は色の分離具合で、小さいほど色が混ざり、大きいほど色がハッキリします。
また、t は色を滑らかに補間するための値で、グラフにするとこんな形状になります。

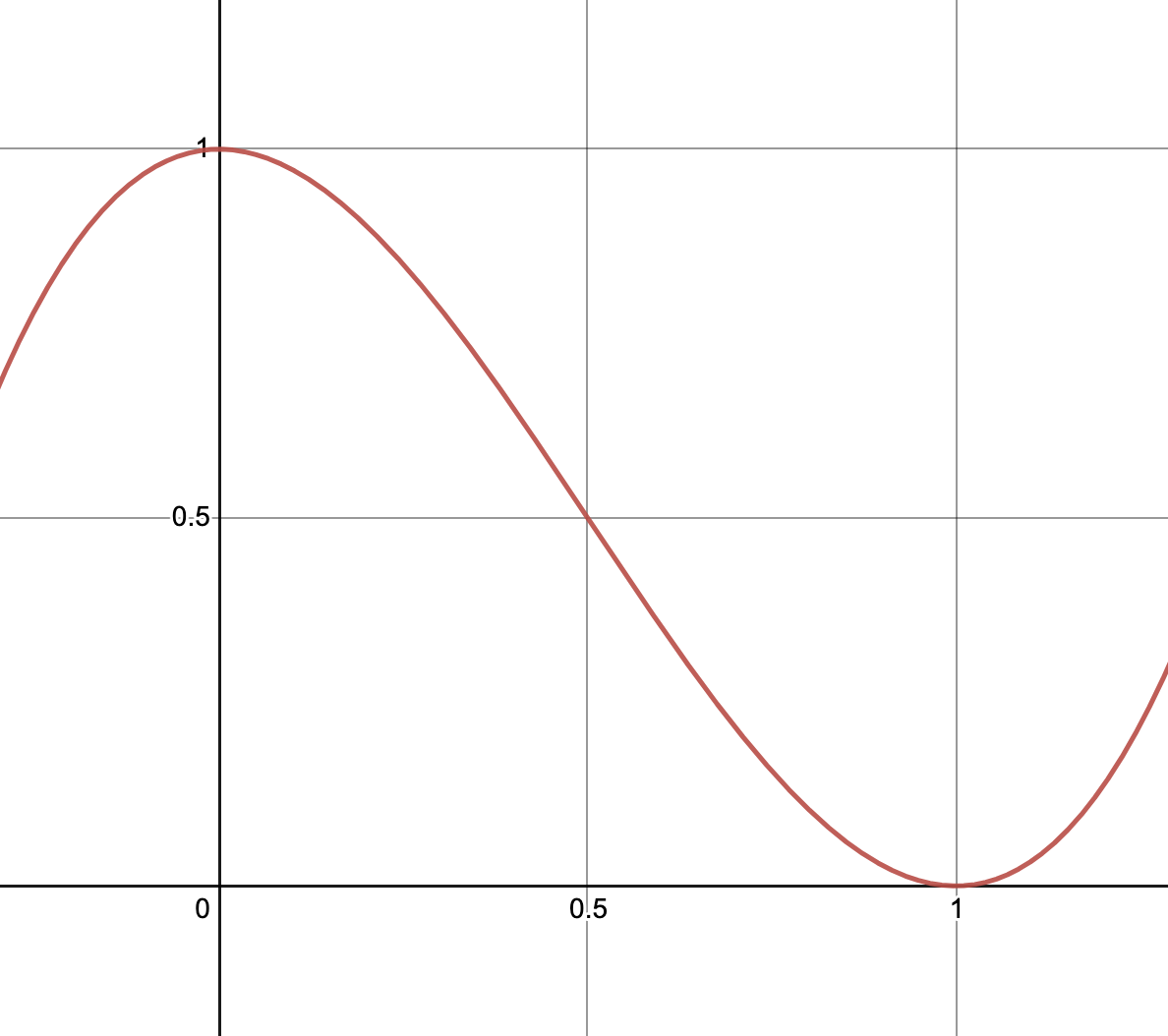
length(sphere.xyz - pos) - sphere.w が球の表面からの距離で、要は球の表面に近いとその球の色の影響を強く受けるようになっているというわけです。

そして、シェーダーに追加した _Colors に値を格納するためのC#コードも追加します。

SlimeRenderer.cs

using UnityEngine;

[ExecuteAlways] // 再生していない間も座標と半径が変化するように
public class SlimeRenderer : MonoBehaviour
{
    [SerializeField] private Material material; // スライム用のマテリアル

    private const int MaxSphereCount = 256; // 球の最大個数（シェーダー側と合わせる）
    private readonly Vector4[] _spheres = new Vector4[MaxSphereCount];
    private SphereCollider[] _colliders;
+   private Vector4[] _colors = new Vector4[MaxSphereCount];

    private void Start()
    {
        // 子のSphereColliderをすべて取得
        _colliders = GetComponentsInChildren<SphereCollider>();

        // シェーダー側の _SphereCount を更新
        material.SetInt("_SphereCount", _colliders.Length);

+       // ランダムな色を配列に格納
+       for (var i = 0; i < _colors.Length; i++)
+       {
+           _colors[i] = (Vector4)Random.ColorHSV(0, 1, 1, 1, 1, 1);
+       }

+       // シェーダー側の _Colors を更新
+       material.SetVectorArray("_Colors", _colors);
    }

    private void Update()
    {
        // 子のSphereColliderの分だけ、_spheres に中心座標と半径を入れていく
        for (var i = 0; i < _colliders.Length; i++)
        {
            var col = _colliders[i];
            var t = col.transform;
            var center = t.position;
            var radius = t.lossyScale.x * col.radius;
            // 中心座標と半径を格納
            _spheres[i] = new Vector4(center.x, center.y, center.z, radius);
        }

        // シェーダー側の _Spheres を更新
        material.SetVectorArray("_Spheres", _spheres);
    }
}

実行してみました。綺麗ですね〜〜

Step6 法線を計算する

次は法線です。法線は面の向きを表すベクトルで、距離関数の値をxyz各軸で偏微分すれば算出できます。
（偏微分は座標をちょっとだけズラして差分を取り、その値をズレの量で割ることで求められます。最終的に正規化するので、コード中では「ズレの量で割る」ということはしておりません）。

法線算出用の getNormal を追加し、一旦法線そのままを色として出力してみましょう。

Step6.Shader（一部抜粋）

+// 法線の算出
+float3 getNormal(const float3 pos)
+{
+   float d = 0.0001;
+   return normalize(float3(
+       getDistance(pos + float3(d, 0.0, 0.0)) - getDistance(pos + float3(-d, 0.0, 0.0)),
+       getDistance(pos + float3(0.0, d, 0.0)) - getDistance(pos + float3(0.0, -d, 0.0)),
+       getDistance(pos + float3(0.0, 0.0, d)) - getDistance(pos + float3(0.0, 0.0, -d))
+   ));
+}

// v2f -> 出力
output frag(const v2f i)
{
    output o;

    float3 pos = i.pos.xyz; // レイの座標（ピクセルのワールド座標で初期化）
    const float3 rayDir = normalize(pos.xyz - _WorldSpaceCameraPos); // レイの進行方向

    for (int i = 0; i < 40; i++)
    {
        // posと球との最短距離
        float dist = getDistance(pos);

        // 距離が0.01以下になったら、色と深度を書き込んで処理終了
        if (dist < 0.01)
        {
-           fixed3 color = getColor(pos); // 色
+           fixed3 color = getNormal(pos); // 色（一旦法線そのままを出力）
            o.col = fixed4(color, 1); // 塗りつぶし
            o.depth = getDepth(pos); // 深度書き込み
            return o;
        }

        // レイの方向に行進
        pos += dist * rayDir;
    }

    // 衝突判定がなかったら透明にする
    o.col = 0;
    o.depth = 0;
    return o;
}

なんとなく立体像が把握できるようになってきましたね。

Step7 リムライトと透明度を実装する

先程計算した法線をもとに、リムライト（物体の輪郭を明るく光らせるアレ）と透明度を実装していきます。

ここで重要になるのは、法線ベクトルと視線ベクトルの内積です。
下の図に示すように、内積の値は輪郭に近いほど0に近づき、輪郭から遠いほど-1や1に近づきます。

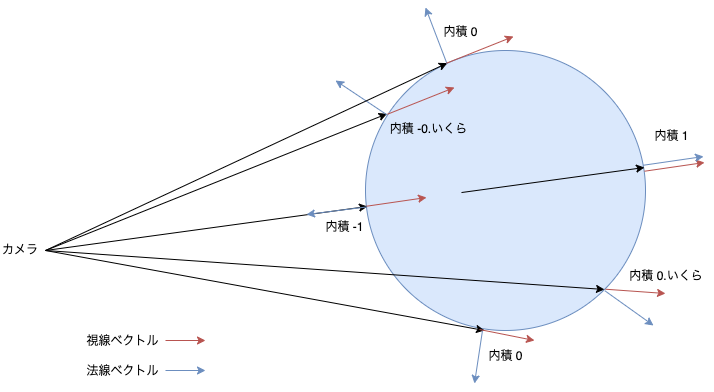
これをうまく使って、
$$ 輪郭らしさ = (1-|法線ベクトル \cdot 視線ベクトル|)^k $$
という0〜1の値をとる指標が導入できます（kは定数）。

さて、シェーダーのコードに落とし込みます。まずは輪郭に近づくほど明るくなるようにします。

Step7.shader（一部抜粋）

// 距離が0.01以下になったら、色と深度を書き込んで処理終了
if (dist < 0.01)
{
-   fixed3 color = getNormal(pos); // 色
+   fixed3 norm = getNormal(pos); // 法線
+   fixed3 baseColor = getColor(pos); // ベースとなる色
+
+   const float rimPower = 2; // 定数
+   const float rimRate = pow(1 - abs(dot(norm, rayDir)), rimPower); // 輪郭らしさの指標
+   const fixed3 rimColor = fixed3(1.5, 1.5, 1.5); // 輪郭の色
+
+   fixed3 color = clamp(lerp(baseColor, rimColor, rimRate), 0, 1); // 色

    o.col = fixed4(color, 1); // 塗りつぶし
    o.depth = getDepth(pos); // 深度書き込み
    return o;
}

ウォォォ光ったぞ

これだと透明感が足りていないので、透明感与えてあげましょう。化粧品のCMかな？
具体的には、計算した輪郭らしさの指標を使って、輪郭から離れるほど透明に、輪郭に近づくほど不透明にします。

Step7.shader（一部抜粋）

// 距離が0.01以下になったら、色と深度を書き込んで処理終了
if (dist < 0.01)
{
    fixed3 norm = getNormal(pos); // 法線
    fixed3 baseColor = getColor(pos);

    const float rimPower = 2; // 定数
    const float rimRate = pow(1 - abs(dot(norm, rayDir)), rimPower); // 輪郭らしさの指標
    const fixed3 rimColor = fixed3(1.5, 1.5, 1.5); // 輪郭の色

    fixed3 color = clamp(lerp(baseColor, rimColor, rimRate), 0, 1); // 色
+   float alpha = clamp(lerp(0.2, 4, rimRate), 0, 1); // 不透明度

-   o.col = fixed4(color, 1); // 塗りつぶし
+   o.col = fixed4(color, alpha); // 塗りつぶし
    o.depth = getDepth(pos); // 深度書き込み
    return o;
}

だいぶいい感じになってきましたね。

Step8 ハイライトをつける

まだちょっとのっぺりしているので、ハイライトを付けてプルンプルンにしてあげます。
詳細は割愛しますが、「頂点⇨ライトへのベクトル」と「頂点⇨カメラへのベクトル」を足して正規化した「ハーフベクトル」というものを使います。このハーフベクトルと法線ベクトルの内積がライトの反射量を表す指標になるので、この値が一定以上のときにハイライトを描画します。
下の図は、ライトの反射がカメラに入りそうなところでは、ハーフベクトルと法線ベクトルの向きが近くなる（つまり内積が1に近づく）という図です。

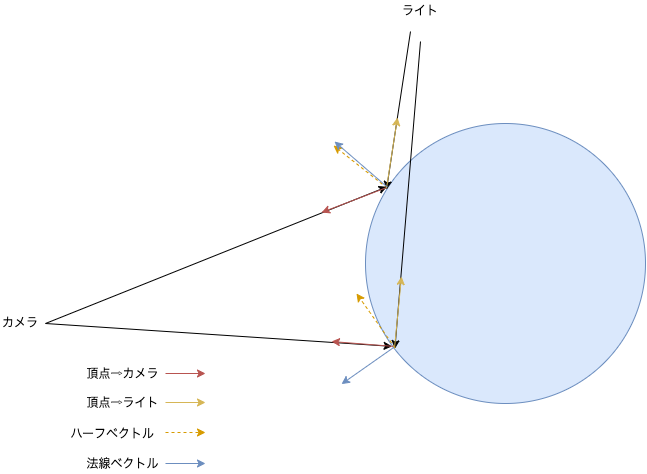
「頂点⇨カメラへのベクトル」ですが、今回は視線ベクトル（変数 rayDir）が「カメラ⇨頂点へのベクトル」を表しているので、それを逆向きにすればいいですね。

シェーダーに落とし込むとこうなります。
ハイライトの部分を明るく不透明にするために、ハイライトとみなされる範囲のピクセルは色と不透明度の値に1を足しています（別に1を足すのではなく1にしてもいいですが）。

Step8.shader（一部抜粋）

// 距離が0.01以下になったら、色と深度を書き込んで処理終了
// 距離が0.01以下になったら、色と深度を書き込んで処理終了
if (dist < 0.01)
{
    fixed3 norm = getNormal(pos); // 法線
    fixed3 baseColor = getColor(pos); // ベースとなる色

    const float rimPower = 2; // 定数
    const float rimRate = pow(1 - abs(dot(norm, rayDir)), rimPower); // 輪郭らしさの指標
    const fixed3 rimColor = fixed3(1.5, 1.5, 1.5); // 輪郭の色

+   float highlight = dot(norm, halfDir) > 0.99 ? 1 : 0; // ハイライト
-   fixed3 color = clamp(lerp(baseColor, rimColor, rimRate), 0, 1); // 色
+   fixed3 color = clamp(lerp(baseColor, rimColor, rimRate) + highlight, 0, 1); // 色
-   float alpha = clamp(lerp(0.2, 4, rimRate), 0, 1); // 不透明度
+   float alpha = clamp(lerp(0.2, 4, rimRate) + highlight, 0, 1); // 不透明度

    o.col = fixed4(color, alpha); // 塗りつぶし
    o.depth = getDepth(pos); // 深度書き込み
    return o;
}

実行すると、こうなります。一気にイキイキしてきました。

Step9 スライム感を上げる

どうもまだスライムではないというか、どうしても球体の部分が目立ってしまっています。
そこで、今まで13個だった球体の個数を一気に100個まで増やします。さらに、球体1つ1つのサイズを半分にします。

さて………どうなるか…

これは間違いなくスライムですね。

更にスライム度を上げていきます。どうも粘性が足りないような感じがするので、粘性を表現してあげましょう。
Angular DragとFrictionを上げてみました。かなりスライム感が出ていると思うのですが、いかがでしょうか。

おわりに

実際にゲームに落とし込むときには、この実装に加えて

• まとまっている感を出すために球体にスライムの重心方向への力を加える
• 負荷を下げるためにスライム部分だけ解像度を下げる

といった追加の処理を行なっています。
それではよきスライムライフを！

参考にしたページ

深度計算

smooth min関数

ハイライト（ハーフベクトル）

色の補間