※このエントリは株式会社NTTデータ数理システム様のセミナー内容に触発されて「自分でやってみよう」で行ったものです。
ここで使うRコードは全てここにあります。
予備知識
金融工学とは
金融工学(きんゆうこうがく、英語:financial engineering、computational finance)は、資産運用や取引、リスクヘッジ、リスクマネジメント、投資に関する意思決定などに関わる工学的研究全般を指す。 金融経済学(financial economics)や数理ファイナンスを理論的バックグラウンドとして持ち、金融機関が事業活動を通じて取り扱う様々なリスクを計測し、適切に管理することを目的として発展した。 (引用元:Wikipedia)
金融工学とは特に投資銀行(GSなど)で2008年前まで大きくバズっていた「クオンツ」達により発展したリスクとリターンのアセスメント、および不確定な状況の中で定期的にリターンを出すために統計学・確率論・応用数学を実運用に乗せたその活動の総体です。
クオンツとは
クオンツは、「Quantitative(数量的、定量的)」から派生した用語で、高度な金融工学の手法を用い、マーケット(市場)の動向などに対して分析や予測を行う業務、またはその専門家のことをいいます。 (引用元:iFinance)
クオンツはいわゆる「金融業界における応用数学者・物理学者・統計学者など科学者の総称」です。流体力学や確率過程、ロケット工学などを前大戦中に研究していた人たちが活躍の場を金融業界に移したのが起こりになっています。いわば「金融業界のアナリスト・エキスパート」職であり、同様の存在にアクチュアリー(保険・年金業界のアナリスト・エキスパート)がいます。
ポートフォリオとは
ポートフォリオ(英語:portfolio)とは、安全資産と危険資産の最適保有率のことである。マクロ経済学の分野からの延長線上として、金融経済学(financial economics)や数理ファイナンスを金融工学と同様に理論的バックグラウンドとして持ち、貨幣市場において金融機関が事業活動を通じて取り扱う様々なリスクを計測し適切なマネージメントを考える上で重要な概念である。(引用元:Wikipediea)
ポートフォリオとは、自分の持っている金融資産(株・保険・不動産・コモディティ・債権など)の按分率のことです。クオンツは金融工学を駆使しリスクを可視化します。それによって投資家は適切なリターンを得たり、レバレッジ(他人資本の借入れによる先行投資)をかけたりするための判断ができるのです。
証券業界におけるリスクの考え方
ボラティリティの大きい商品は「リスク」である
一口に金融商品と言っても株・保険・不動産・コモディティ・債権など多岐に渡りますが、卑近な例として株価を例にしてボラティリティがどのようにリスクとみなされるのかを説明していきます。実際に使用している環境は下記になります。
ハード:MacBook Pro (2016)-メモリ 2G-Core i5
ツール:R-Studio Version 1.0.44
ライブラリ:quantmod(株価取得用)とquadprog(最適化問題ソルバー)、他一般的なデータハンドリングライブラリ(dplyrなど)
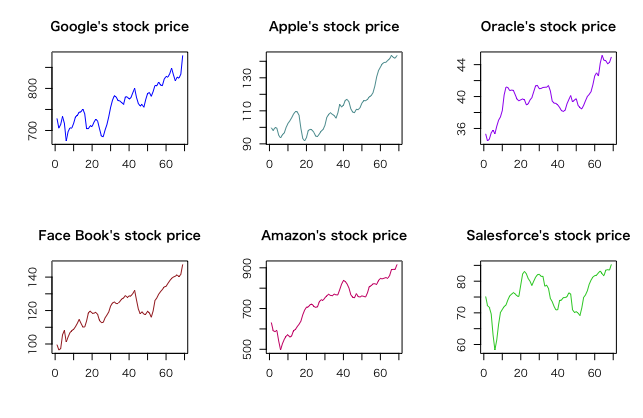
実際に見ていきましょう。試しにquantmodを使ってGoogleFinanceから6つのTechGiantsを取り出します。期間はとりあえず2016年1月1日〜2017年4月30日、週次のデータを取り出して、適当にプロットします。
横軸が週次のインデックス(一般的?に金融工学では時間軸は考えないらしいのでそれに準拠しています)、縦軸が株価になります。6つを見た限り、程度の差こそあれ、この期間は常に上り調子であった事が見て取れます。
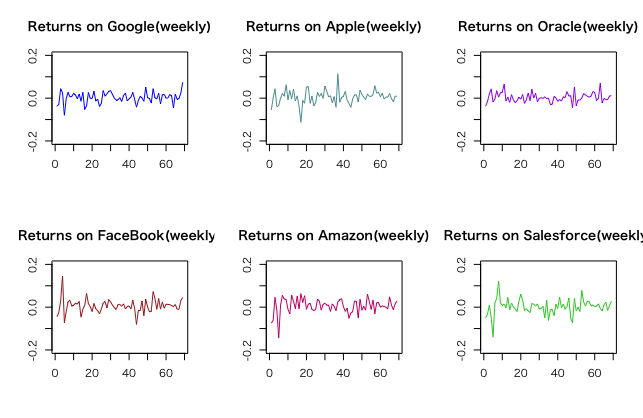
こうしてみると、FBやAmazonは安定して上昇している感じがします。それに対してOracleやSalesforceは大きな下落局面や踊り場があったりと、投資するにはリスクが大きそうです。では、この価格の違う6つの商品を同じ俎上に載せてリスクを比較するにはどうすればいいのか?例えば、100口買った時の投資に対するリターンの割合を見てみるのがいいかもしれません。
これをみるとOracleが安定しているように見え、Appleは比較的変動が激しく見えます。この様に、金融工学は株価の変動=ボラティリティを判断します。
金融工学においてボラティリティ(volatility)とは、広義には資産価格の変動の激しさを表すパラメータ。広義については、テクニカル指標一覧#広義ボラティリティを参照。狭義には株価の幾何ブラウン運動モデル
$ dS_t = S(t)(\sigma dW(t) + \mu dt) $
における $\sigma$ のこと。シグマ。(引用元:Wikipediea)
この様に、ボラティリティ=シグマを計算してそれが大きい場合はリスクであるととらえます。
株価データからボラティリティを抽出する
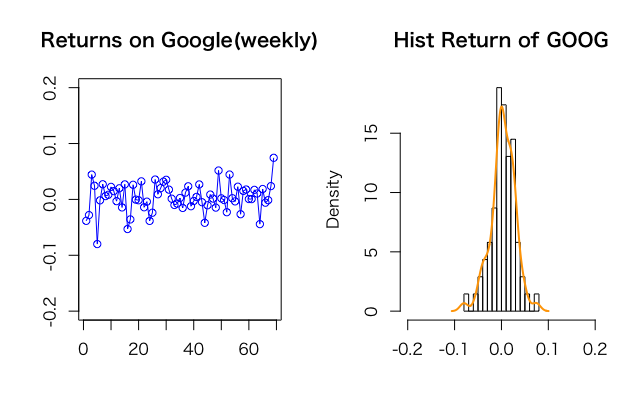
では、時系列データからどの様にして$\sigma$ を取り出すかを説明します。Googleのリターンで見て見ましょう。
まず、金融工学では時系列データを時系列データではなく、ざっくりと「ある一定期間に取れたサンプルの集合」と考え、時系列のラベルを取ったのが左下の図です。この取れたサンプルデータを縦軸の方から見ると(ここはイマジネーションが必要ですが)、”0.0”を中心に上下にぶれていると考えられます。これらひとつひとつのサンプルをヒストグラム状にプロットしたのが右下の図です。
この様にヒストグラムにすると $\sigma$ =ボラティリティが大きい方がリスク(つまりばらつきが大きいのは悪)と言う事が理解しやすいかと思います。
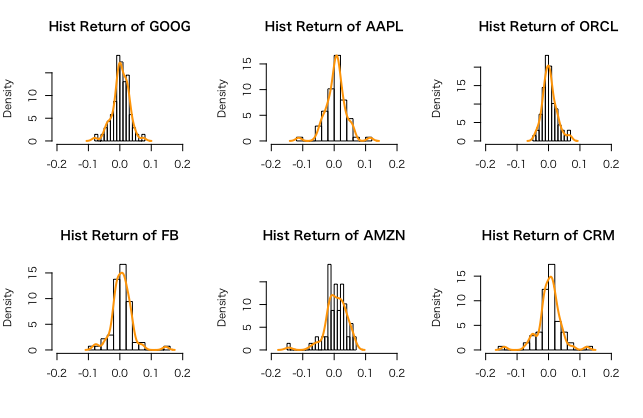
参考までに、6つのTech Giantsのヒストグラム、および平均リターン $\mu$とボラティリティ$\sigma$を比較のために載せておきます。

こうして見ると、Oracleのボラティリティが小さいのがよく分かります。リターンもそこそこです。翻って、Salesforceはリターンが低く、ボラティリティが大きい、あまり優良でない資産と判断できます。
ポートフォリオ最適化
素朴に手でやってみよう
ポートフォリオ最適化を理解するには、時系列データをヒストグラムと見る作業に加え、もうひとつの思考のジャンプが必要です。それは株価を上下する波とみなす事です。
株価を波と考えると、三角関数の重ね合わせで波の形が変わった様に、株価の重ね合わせで新しい波=新しい株を作れると考える事ができます。
では、株価をどの様に重ね合わせるとリスクがどう変動するのか?実際に簡単な例でやってみましょう。
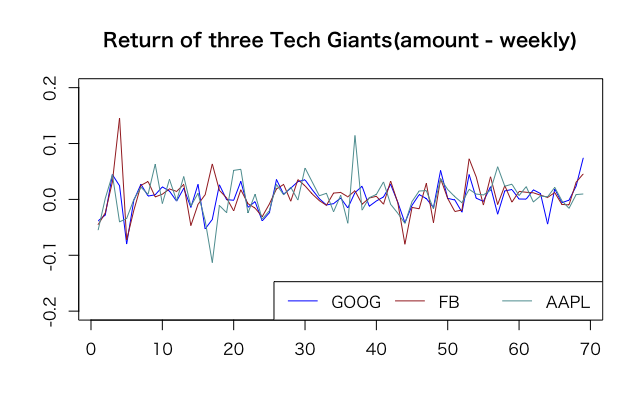
簡単のために、今回は3つ(Google/FB/Apple)の株価にそれぞれ手持ちを1/3ずつ分散投資して、ボラティリティを下げられるか見て見ます。ここでやっていることを波に例えると、波の上下幅を1/3にして、重ね合わせる事になります。
3つの株だけを1つのチャートに乗せるとこうなります。
新しくブレンドされた株”BLND”はこちら。
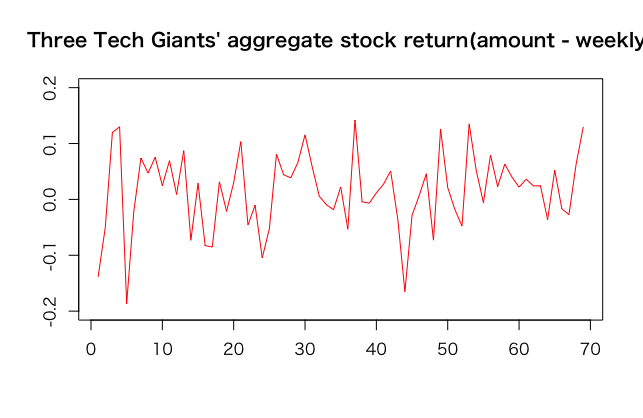
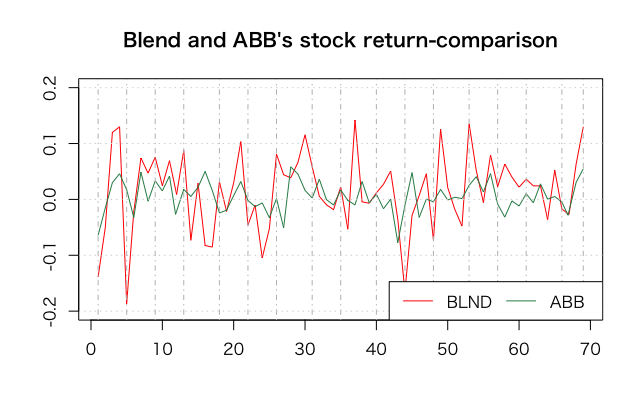
・・・あまりリスクが減った様に見えませんね。それでは3つではなく、もう一つ混ぜ込んではどうでしょうか?その時は特に、波が逆に動いている(テクノロジー系企業と株の動きが連動していない)株がいいでしょう。例えば、ABBグループ (Asea Brown Boveri、アセア・ブラウン・ボベリ)と言うスイス発の重工業コングロマリット株があります。
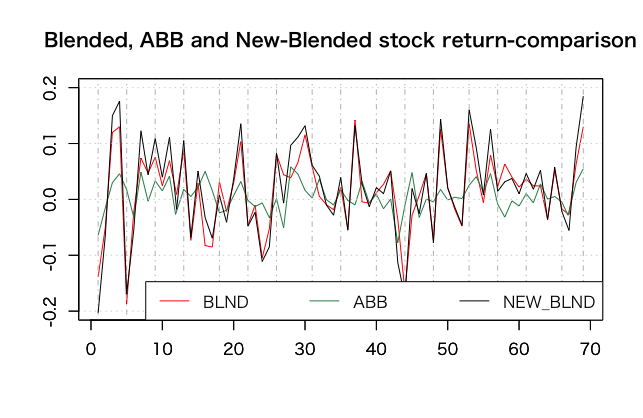
上の画像を見てのなんとなくですが、動きはBLNDと連動していない感じがします。これを混ぜ込んで見ましょう。
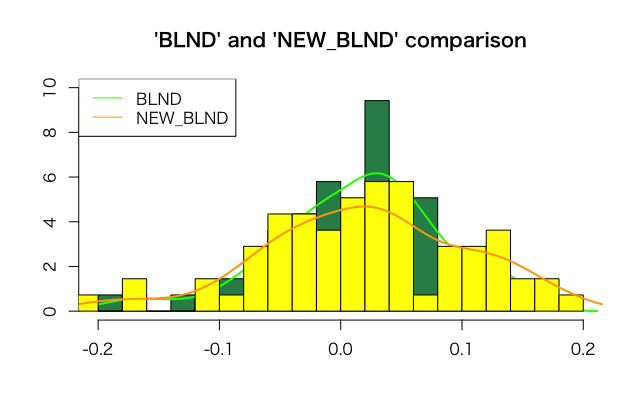
上の黒い線が新しくABBを混ぜ込んだNewブランドになります。ヒストグラムでも重ねて比較して見ましょう。
平均リターンが減り、ボラティリティが大きくなっています。つまり失敗したことになります。
なぜ失敗してしまったのでしょうか?
例えば「ニューヨーク市場の株は程度の差こそあれ全て同じ方向に動く」と言う仮説が立てられます。所詮はひとつのシステムの中にいる同じ穴の狢ということですね。
もしもこの仮説が正しかった場合、回避策は別の証券取引所(欧州や日本)の株に範囲を広げてポートフォリオ最適化を行う事になります。これが素朴な手段でのポートフォリオ最適化です。
しかしながら、人力でやるには限界があります。そこで、金融工学の出番です。
モデルを使ってやってみよう
ポートフォリオ最適化の考え方として「分散最小化」「絶対偏差最小化」「CVaR」「VaR」などがあります。今回は分かりやすさ優先で、分散の最小化を行う最適化モデル「Markovitzモデル」で6つのポートフォリオの最適化を行います。
Markovitzモデル(分散の最小化)
Markovitzモデルを定式化すると下記の様になります。
\begin{eqnarray}
\min \,\,\,\,\,\,\,\,\,\,\,\,x^tQt \\
subject \,to \,\,\,\,\,\,\,\, \\
\sum_{i \in A}x_i &=& 1 \\
x_i &\geq & 0 \\
\forall x_i &\in& A
\end{eqnarray}
モデルの説明はそのうちどこかでやることにして、
これを元に、Rの"quadprog”ライブラリーで解きます。
詳しいコードは ここにあげています。
これを元にすると
GOOG=3.8%
FB=13.8%
APPL=19.2%
AMZN=7.7%
ORCL=53.3%
CRM=2.3%
となり、オラクルへの投資割合が50%を超えました。このモデルではオラクルが優良資産だと判定される様です。ヒストグラムも、

となり、オラクルに近い形でポートフォリオが組まれているのが分かりますね。
実際には、分散だけ最小化させても、期待リターンが無いと儲けに繋がりません。
なので、もう少し込み入ったモデルを使うことは最後に付記しておきます。
このモデルでいうと、最近パッとしないオラクルは、パッとしないからこそとても安全なのですね。