この記事ではSIGGRAPH2016で発表されたErosion Thickness on Medial Axes of 3D Shapes¹ を解説し、実際に実装しています。

はじめに

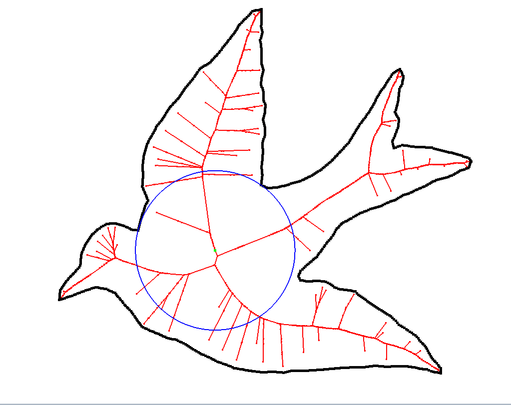
CGの世界には、Medial Axisというものがあります。Medial Axisは、とても大雑把に言うと「その図形の骨格」です（Topological Skeletonとも言われます）。

2Dであれば、上図の赤い線がそれにあたります。青い円を見ると、鳥の首と右翼の付け根あたりで外周と接していることがわかります。このように外周と2点以上で接している円を「接触円」と呼び、Medial Axisはこの接触円の中心の軌跡になっています。

3Dでも同様に、物体の表面と2点以上で接している球の軌跡がMedial Axisになり、その形状は曲面になります。

Medial Axisはその形状の大体の「骨格」なので、画像や3次元形状を処理する時に形状を単純化したり、3次元モデルの変形に使ったり、といった時に役に立ちます。

このMedial Axisの普遍的な課題として「どの軸を『メインの軸』とすべきか」、つまり「重要な軸を決定する」タスクがあります。例えば上の鳥の例では、両翼を通る軸と、頭と尾を通る軸の二つが「メインの軸」になりそうです。

2Dの図形のMedial Axis上のある点の重要度を決めるタスクは、Erosion Thickness（後述）という値を求めることが有効らしいということがわかっています。上の3つはそれぞれ「接触円の2接線の角度」「接触円の半径」「Erosion Thicknessの値」でそれぞれMedial Axis上の点を色付けしたもので、下の3つはある閾値以上の点のみを抽出したものです。角度の場合は（馬の毛のような）極端に鋭い表面部分に反応したり、軸が途中で途切れてしまっていたりします。また、半径の場合は馬の足のように細い部分になっているところが切れてしまっています。一方で、Medial Axisによる色付けはうまくいっています。

しかし、3Dの形状のMedial Axis上の点の重要度を求めるタスクは、長らく有効な手法が見つけられていませんでした。唯一有効っぽい手法 ⁴は、多面体上の全ての2面のペアの距離を求めなければならず、計算量が $O(n^2)$ になっていました。

そこで、この論文ではErosion Thicknessを3DのMedial Axisに応用する手法を提案しています。これにより、3D形状のMedial Axisの内「重要な骨格」を抜き出すことに成功しています。また計算量も、3Dモデルの頂点の数を$A$、点の数を$N$とすると、 $O(|A|log|N|)$ に抑えることができています。

2DのErosion Thickness

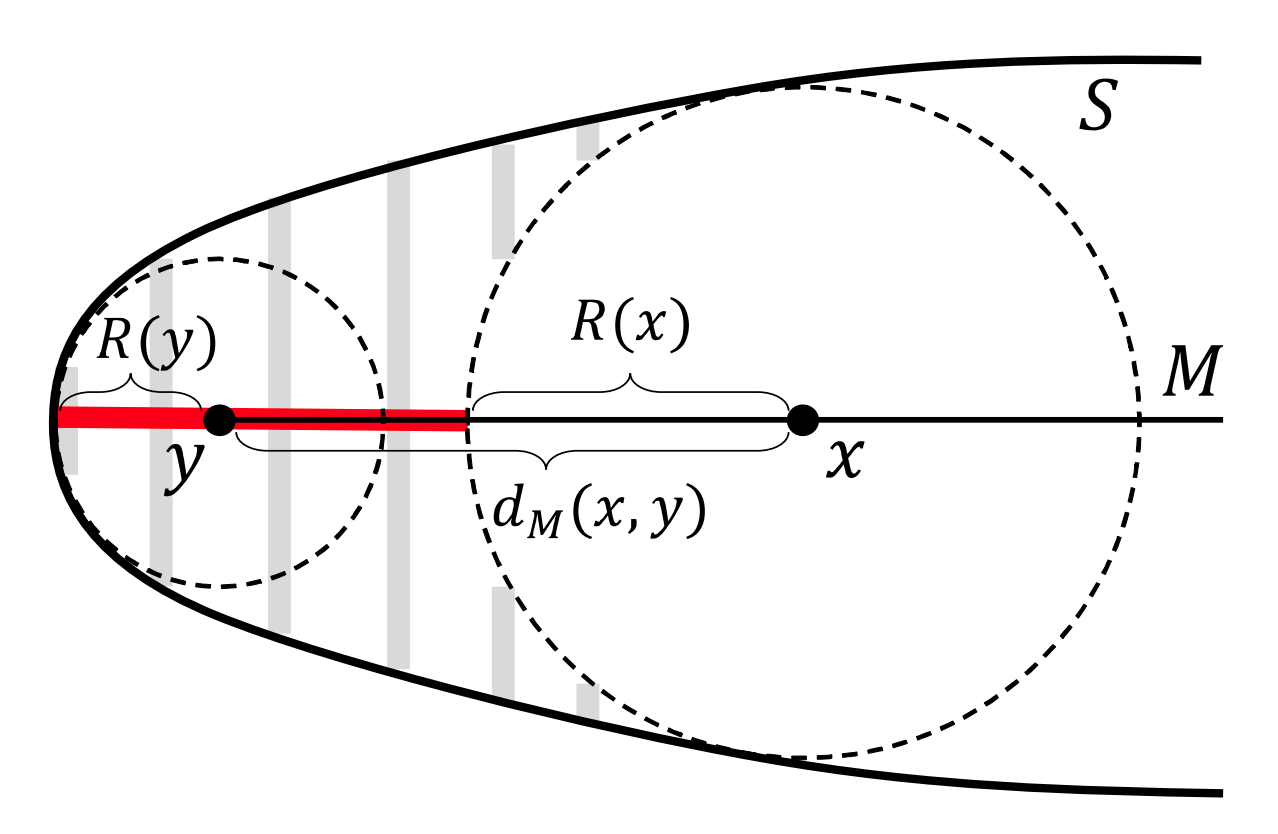
まず、既存の2DのErosion Thicknessを用いる手法を概観します。上の図中の $S$ は曲線の外周で、 $M$はMedial Axisです。図中の $y$ はMedial Axisの端点で、 $R(y)$は$y$における接触円の半径です。ここで、$M$上の点 $x$を選び、$y$からの$M$上の距離を$d_M(x, y)$と表します。

この時、$x$におけるErosion Thickness $ET(x)$ は、上の図中の値を用いて

ET(x)=R(y)+d_M(x, y) - R(x)

と表されます。これを分岐のあるMedial Axisに対しても一般化するため、先行研究 ⁵ では Burning Time というものを定義しています。まず、Medial Axisが全て可燃性の線香のような素材でできていると考えます。この時、Medial Axisの各終端点（上図でいう$y$）に$R(y)$秒後に点火します。点火した炎は1秒あたり1の距離で進むものとします。もしこの炎が分岐点に到達した場合、「分岐点の枝分かれが一つを除き全て燃え尽きるまで」その先に進むのを待ちます。もしこれが満たされたら、炎は残った一つの枝分かれの方に進んでいきます。

ここで、$M$上の各点に何秒後に炎が到達するか（Burning Time）を$BT(x)$と表せます。そして、この場合、$ET(x)$は

ET(x) = BT(x) - R(x)

で表されます。要するに、Medial Axisと各点における接触円の半径がわかれば、Burning Timeを求めるだけで（？）Erosion Thicknessを求めることができるのです！

3DのBurning Function

筆者は2DでのErosion Thicknessの理論を応用し、3DのMedial Axis上におけるErosion Thicknessも「Burning Timeと接触球の半径の差である」と定義しています。しかし、3DのMedial Axisは曲面になっていて、2Dのような曲線とは勝手が違いそうです。

3Dの曲面状のMedial Axisの場合、Medial Axisの端を $\partial D$ とおけば、上の点 $y$ とその点における接触円 $R(y)$ は定義できそうです。また、Medial Axisが一枚のシート状であれば、その上の点 $x$ におけるBurning Timeの値 $BT(x)$は、$y$からの$M$上の距離を$d_M (x,y)$と表すと、

BT(x) = \min \{d_M(x,y) + R(y), y \in \partial D \}

と表せます。

分岐点

ここで問題になるのが分岐点の扱いです。2DのBurning Timeでは

もしこの炎が分岐点に到達した場合、「分岐点の枝分かれが一つを除き全て燃え尽きるまで」その先に進むのを待ちます。

と書いたように、炎が「止まる」動作が定義されています。

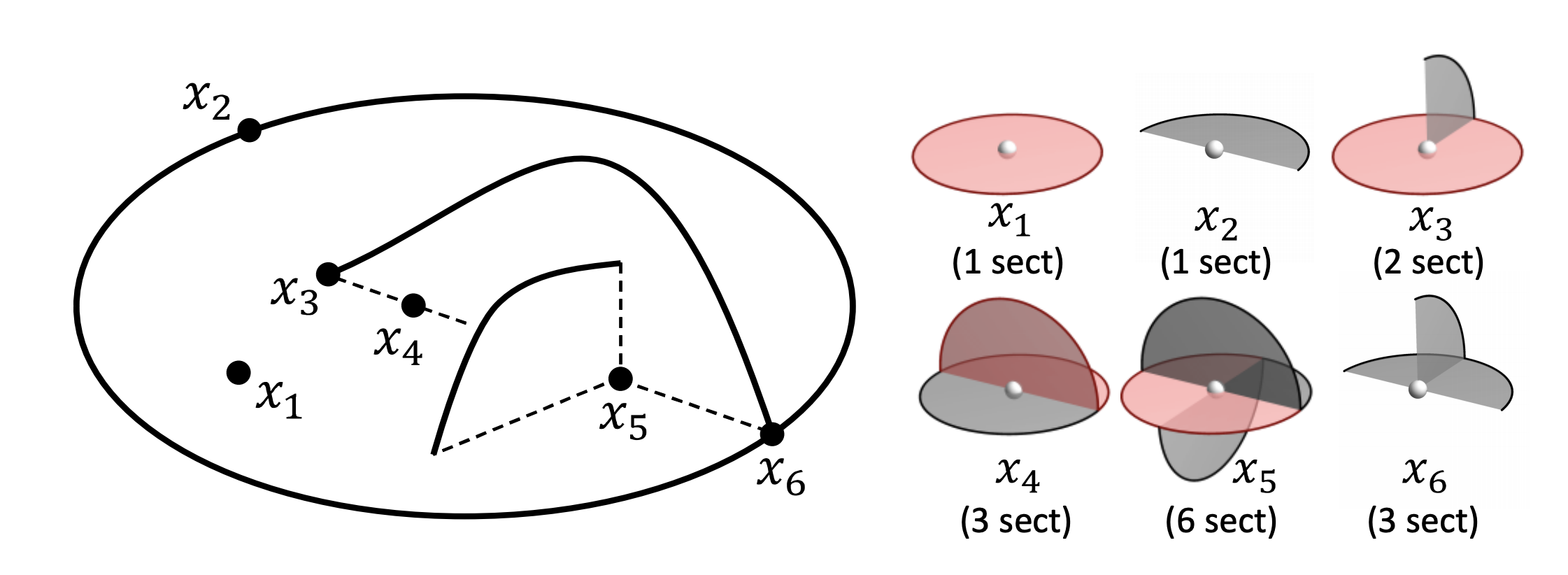
これを3Dで再現するために、論文ではSectorという概念を定義しています。Sectorは、点に隣接する面のトポロジーを表したものです。
もし点に隣接する面の集合が一枚の円盤の同じトポロジーとみなせる場合（上図右の $x_1$ と $x_2$）は、その点のSectorは1つです。一方で、その点で複数の面が交差しているような場合（上図右の $x_3$ 〜 $x_6$）には、各面同士の交線で全ての面を切断した結果得られるパーツがSectorになります。例えば、$x_3$の場合は中心点から上に伸びている面と中心点の周りを囲む面の交線で周囲の面を分割でき、それぞれがSectorを形成します。
先行研究により、（理想的な）Medial Axis上の点の周りの面のトポロジーは、上図右の6種類しか存在しないことが示されているので、点の周りでのSectorの数は1,2,3,6のいずれかの値をとるということになります（今回用いたテストデータではこれに当てはまらないトポロジーの点も存在しましたが…）。

このSectorを使えば、2Dの「分岐点の枝分かれが一つを除き全て燃え尽きるまでその先に進むのを待つ」操作を表現できます。
本研究では、炎がSectorが2つ以上の点に到達した場合、「一つを除いて全てのSector経由で炎が到達するまで」その先に進むのを待つようにしています。

ポリゴンモデルにおける実装

世の中に存在する3Dモデルのほとんどはポリゴンモデルで構成されています。3Dモデルを大きく拡大すると三角形の面が現れるのを見たことのある方も多いでしょう。

このポリゴンモデルで「炎を燃やす過程」を再現するため、本研究ではMedial Axis上の各点 $N$ と、ポリゴン上の辺 $A$ を用いてグラフ $G$を構成しています。

グラフは以下の疑似コードで表したような3種類の要素で形成されています。

// 点
interface Vertex {
  radius: number // その点における接触円の半径
  time: number // その点におけるburning timeの値。デフォルト値は無限
  burned: boolean // Burning Processの結果燃やされたかどうか
  sectors: Sector[] // その点におけるSector
  primeSector: Sector // その点におけるSectorのうち、経路として採用されたSector
}

// Sector
interface Sector {
  time: number // そのSectorのburning timeの値
  burned: boolean // そのSectorがBurning Functionの結果燃やされたかどうか
  arcs: Arc[] // Sectorに含まれる辺
  primeArc: Arc // Sectorに接続している辺のうち経路として採用された辺
}

// 辺
interface Arc {
  length: number // ノード間の距離
  vertices: [Vertex, Vertex] // 辺を共有している2点
}

このグラフに対し、Dijkstra-likeに各点のBurning Timeを決定します（詳しいアルゴリズムは論文をご覧ください…）。

実装

今回はこのBurning Processをpythonで実装しました。実装はこちら。

下準備

まず、グラフ $G$ を以下のコマンドにより作成します。コマンドの第2引数がmedial axisのplyファイル、第３引数が元の3Dモデルのplyファイルです。

$ python main.py ./models/hand_ma.ply ./models/hand.ply

plyファイルは各点のxyz座標と全ての面の情報を保持しているので、それを元に各点のSectorを算出して、グラフを作成します。

graph.py

    vertices = pd.DataFrame(datadict['coords'])  # 1 DataFrameの作成
    vertices['index'] = vertices.index
    vertices['burned'] = False
    vertices['primeSector'] = None # 2 初期値をセット
    vertices.loc[:, 'faces'] = vertices.index.map(getFaces) # 3 各点に隣接する面をセット

    vertices.loc[:, 'sectors'] = vertices.apply(getSectors, axis=1) # 4 各点に隣接する面の情報から、Sectorを算出

    vertices.loc[:, 'time'] = vertices.apply(getTime, axis=1) # 5 接触円の半径を算出

    vertices.loc[:, 'sectorTime'] = vertices.sectors.map(getSectorTime)
    vertices.loc[:, 'sectorBurned'] = vertices.sectors.map(getBurned)
    vertices.loc[:, 'sectorPrimeArc'] = vertices.sectors.map(getPrimeArc) # 6 Sector関連の初期値をセット

    vertices.to_pickle('./tmp/complete-vertices.pickle') # 7 一時ファイルとして保存

接触円の半径は、「元の3Dモデル上の最近傍点」を求めることにより得ています。

Burning Function

次に、生成されたグラフに対してBurning Processを実行します。

$ python queue.py

Erosion Thickness

次に、$ET(x) = BT(x) - R(x)$ により各ノードにおけるErosion Thicknessの値を計算します。コマンドの第2引数は元の3Dモデルのplyファイルです。

$ python export_ply.py ./models/hand.ply

plyファイルの生成

最後に、plyファイルを生成します。このplyファイルは、各頂点のErosion Thicknessの値に応じて色の情報を持っています。

$ python export_ply.py

結果

著者が公開している手の3Dモデルを用いて実行しました。

生成されたplyファイルをblenderでレンダリングした結果、以下のようになりました。

Erosion Thicknessの値が大きい部分を赤で、小さい部分を青で表示しています。手のひらの真ん中あたりの骨格として適切そうな部分が赤くなっていて、概ね良さそうな感じがします。

比較のため、Radius Functionの値で色付けしたものと並べてみました。

Radius Functionは薬指の付け根あたりが中心でないと判定されてしまう一方で、Erosion Thicknessなら全体からみた「芯の位置」を検出できていることがわかります。

感想

点の周囲をSectorに分割するタスクが思いの外大変でした。

点の周辺の面のトポロジーは理想的なMedial Axisでは6種類となっていましたが、面が縮退しているようなものや、「やばい接続の仕方」をしている面を分割するのが大変でした。

あと、このアルゴリズムの実行には元の3DモデルとMedial Axisの3Dモデルの両方が必要なのですが、Medial Axisの生成に使用しようと思っていたライブラリのコンパイルが通らなかったので、この手の3Dモデルでしか実行ができませんでした…😇

この記事は東京大学の講義「映像メディア学」（https://www.hal.t.u-tokyo.ac.jp/~yamasaki/lecture/index.html ）の最終レポートも兼ねています。

Yajie Yan, Kyle Sykes Erin Chambers, David Letscher, Tao Ju. Erosion Thickness on Medial Axes of 3D Shapes. ACM Transactions on Graphics, SIGGRAPH 2016. DOI:https://doi.org/10.1145/2897824.2925938 ↩
http://pages.cs.wisc.edu/~csverma/CS558_11/MedialAxis.html ↩
Tamal K. Dey, Hyuckje Woo, and Wulue Zhao. 2003. Approximate medial axis for CAD models. In Proceedings of the eighth ACM symposium on Solid modeling and applications (SM ’03). DOI:https://doi.org/10.1145/781606.781652 ↩
Tamal K. Dey and Jian Sun. 2006. Defining and computing curve-skeletons with medial geodesic function. In Proceedings of the fourth Eurographics symposium on Geometry processing (SGP ’06). ↩
Lu Liu, Erinn W. Chambers, David Letscher, Tao Ju. 2011. Extended grassfire transform on medial axes of 2D shapes. Computer-Aided Design. DOI:https://doi.org/10.1016/j.cad.2011.09.002 ↩

Erosion Thickness on Medial Axes of 3D Shapesを実装してみた