アルゴリズム 体操１

Binary Search on Arrays

説明

ソートされた整数を保存するArrayと探してるキーが渡されて、もしそのキーがArrayの中にある場合はキーのIndexを返す。もし、そのキーが無ければ-1を返す。

例

キーが47で要素20個を保持するArray

Solution

Runtime Complexity: O(logn)

Memory Complexity: O(logn)

Binary Searchは、ソートされた配列内の要素のインデックスを見つけるために使用されます。 要素が存在しない場合もそれも同様に効率的に見つけることが出来ます。アルゴリズムは、各ステップで入力配列を半分に分割していきます。すべてのステップの後、探しているインデックスが見つかったかどうか、配列の半分を破棄できます。 したがって、解はO（logn）時間で計算できます。

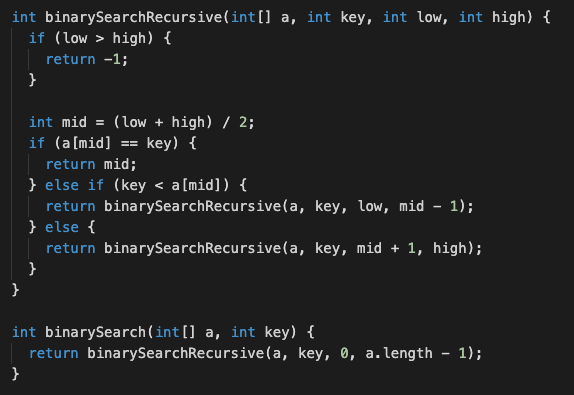
大まかなアルゴリズムの流れ

1. Arrayの調べる範囲である、一番小さいインデックスのlowと一番大きいインデックスのhighを決める。
2. そのlowとhighから中間地点のmidの値を求める。
3. もし、midのインデックスにある要素がキーと同じであればmidを返す。
4. もし、midのインデックスにある要素よりも大きい場合はhigh = mid - 1。（lowはそのまま）
5. もし、midのインデックスにある要素よりも小さい場合はlow = mid + 1。（highはそのまま）
6. ただ、low が　high　よりも大きくなってしまったらキーは存在していないことになるので - 1を返す。

code

補足

Recursive ではなく、While loopを使うIterative の方法だと速度効率は同じですが、Space Complexity がO(１)と出来ます。