フリーの統計解析ソフトRは、簡単な統計分析から機械学習系のライブラリまで、多様な機能を備えていますが、よく使われるのは頻度論的な多変量の解析なのではないかと思います。
(重回帰分析とか主成分分析とか、そういうやつです)
そして、多変量解析を始めるにあたっての最初のステップは「変数間の関係を把握する」ことです。
今日は、Rの多様なグラフィカル表現の中から、多数の変数の関係をパッと把握するのに気軽に使えるものを紹介します。
紹介する機能一覧
①リッチな散布図を作る
②散布図行列で全変数のペア同士の関係を一望する
③条件付きプロットを作る
リッチな散布図を作る
どんなデータを扱うにしても、とりあえず散布図を描いてみると良いというのはよく言われるところです。
その際大事なのは「一目で情報の全体感がつかめる」ことだと思います。
ここでは、多変量データの中から2変量を選んで
・散布図
・回帰直線
・片方の変数のヒストグラム
・もう片方の変数の箱ヒゲ図
の4つを一気に書きます。
※以下では、Rの組み込みデータの中から簡単なものとしてtrees(アメリカ桜の周囲、高さ、木材量のデータ)を使います。
attach(trees) //扱うデータを固定
names(trees) //含まれている変数を確認
par(fig=c(0,0.7,0,0.7)) //グラフを描く領域を指定
plot(Height,Volume, lwd =2) //散布図を描く
abline(lm(Volume ~ Height), lwd =2) //回帰直線を描く
lines(lowess(Volume~Height),lwd =1) //局所重み付き回帰直線を描く
par(fig=c(0,0.7,0.65,1),new = TRUE) //ヒストグラムを描く位置を指定
hist(Height, lwd =1) //ヒストグラムを描く
par(fig=c(0.65,1,0,0.7),new = TRUE) //箱ヒゲ図を描く位置を指定
boxplot(Volume, lwd = 2) //箱ヒゲ図を描く
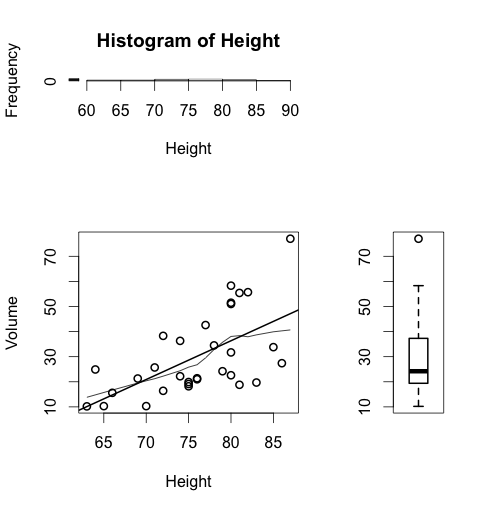
そうするとこんな図になります。
局所重み付き回帰直線とは、ここでは
y_i = g(x_i) + ε_i
という形の方程式です。
gは平滑化関数、εは平均0・分散定数のランダム定数で、要するに
単なる最小二乗法による線形回帰のムリなあてはめを緩和する効果を持ちます。
グラフのぐにゃっと曲がっているラインです。
散布図行列で全変数のペア同士の関係を一望する
上のサンプルは多変量変数の中から特定のペア(VolumeとHeight)を選んで作ったものですが、すべての組み合わせについて一望するやり方もあります。
(まあ、多変量といってもこのやり方だと5、6変数までが限界ではあるのですが。。)
とっても簡単です。
pairs(trees,panel = function(x,y)
{abline(lsfit(x,y)$coef, lwd = 2) //回帰直線を加える
lines(lowess(x,y), lty = 2, lwd = 2) //局所重み付き回帰直線を加える
points(x,y)})
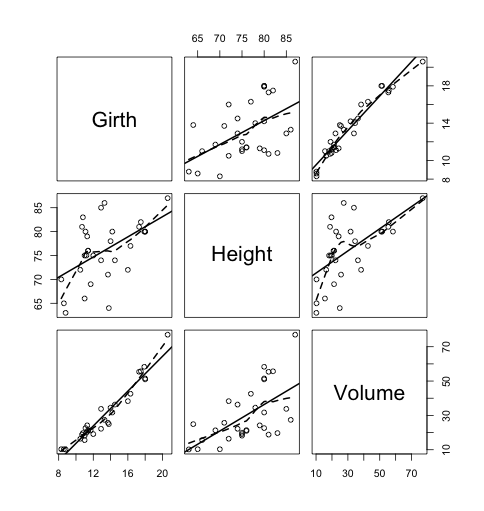
そうするとこんな感じになります。
これで全体を一望して
・各変数間に相関があるか
・外れ値はあるか
・変数がクラスターをなしているか
みたいなポイントをパッとチェックするわけです。
条件付きプロットを作る
最後に、条件付きプロット(コプロット)を紹介します。
これは、複数ある変数のうち一つの値を一定のレンジごとに固定して、
その範囲内で、残った変数のペアの関係を見るものです。
コードはこんな感じになります。
coplot(Volume~ Height | Girth,
panel = function(x,y,col,pch)
panel.smooth(x,y,span=1))
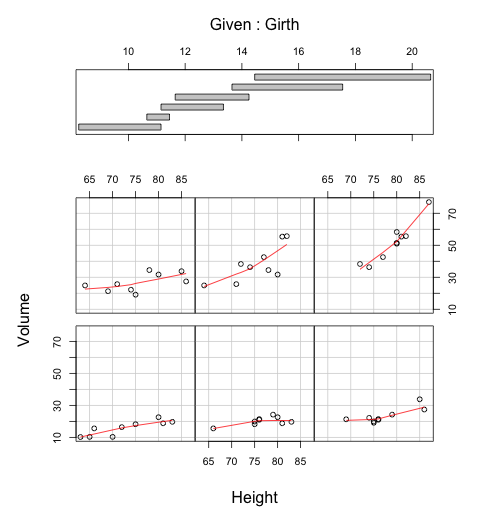
ここでは、Girthを固定して、Girthの取る各レンジごとに、
HeightとVolumeの関係を視覚化しています。
図では、HeightとVolumeの局所重み付き回帰直線を加えてあります。
こうすることで、Girthのレンジに応じて、HeightとVolumeの相関関係に変化があるかどうかを確認できます。
というわけで、簡単ですが、3つのグラフィック化方法を紹介しました。
Rのグラフィック表現には色々なヴァリエーションがありますが、この3つだけでも、変数間の関係を見る最初のステップしてかなり役にたつと思います。