はじめに
この記事は、42tokyo Advent calendar 2020の15日目の記事になります。どの記事も面白いです。先日はhyudaiさんが「日食なつこは冬に合う」という題で記事を書いてくださっています。
ここ数日は技術系の記事がなかったのでちょっと勉強できるような内容の記事を書こうと思い差分法を題材とさせていただきました。
間違い等がございましたら教えていただけたら嬉しいです。
差分法とは
差分法はコンピュータ計算手法の一つで、微分方程式を近似解を得る手法の一つです。
$x$の関数$f(x)$において、有限値$h$とすると${\it \Delta}f(x) = f(x + h) - f(x)$を$f(x)$の差分と言います。この差分を繰り返し求めていくことで近似解を得ます。問題よって精度と計算量の見合った手法を選びます。
流体力学、分子動力学などのシミュレーションやカオス力学などで用いられています。
オイラー法による三角関数の計算
ここでは、オイラー法と呼ばれる1次精度の差分法を用いて解析解のある$df(x)/dx = \cos(x)$を求めます。微分して$\cos(x)$となるのは$\sin(x)$です。解析解があるので差分法の数値解と解析解を比較してみます。
$t_0$の時の初期値$y_0$とするとオイラー法は次の式で定義されます。$dt$刻み幅です。
$$
y_{n+1} = y_n + dt\cdot f(t_n, y_n)
$$
プログラム
import matplotlib.pyplot as plt
import numpy as np
plt.figure()
x=0
dt=0.01
t=0
xp = []
tp = []
for i in range(1000):
x += np.cos(t)*dt
t += dt
xp.append(x)
tp.append(t)
plt.scatter(tp, xp, c='b', label='Numerical')
t = np.linspace(0, 10, 100)
plt.plot(t,np.sin(t), label='Analytical', c='r')
plt.legend()
plt.grid(which = "major", axis = "x", color = "gray", alpha = 0.75, linestyle = "--", linewidth = 1)
plt.grid(which = "major", axis = "y", color = "gray", alpha = 0.75, linestyle = "--", linewidth = 1)
plt.show()
出力結果
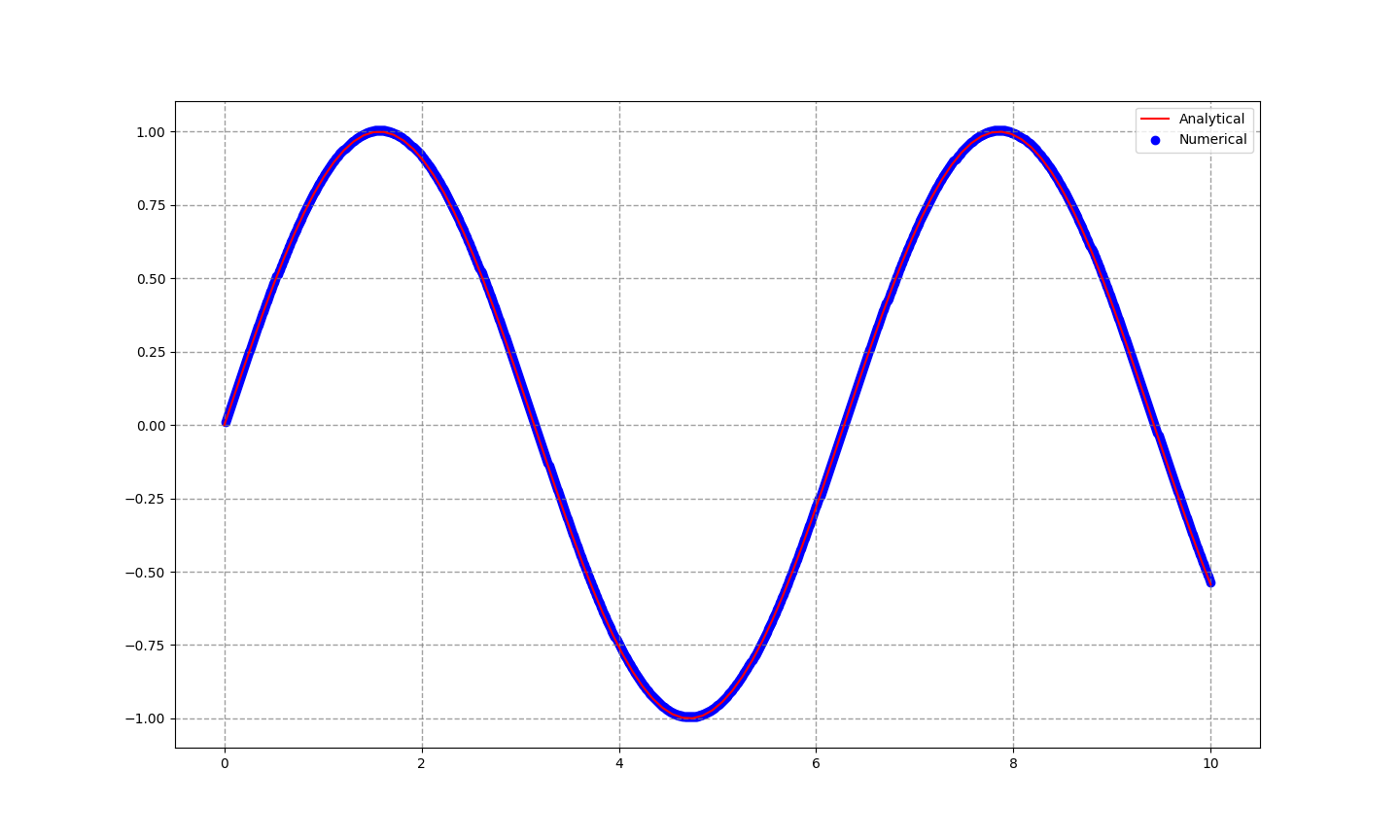
解析解と完全にフィットしています。さて、刻み幅$dt$を荒くしてみましょう。
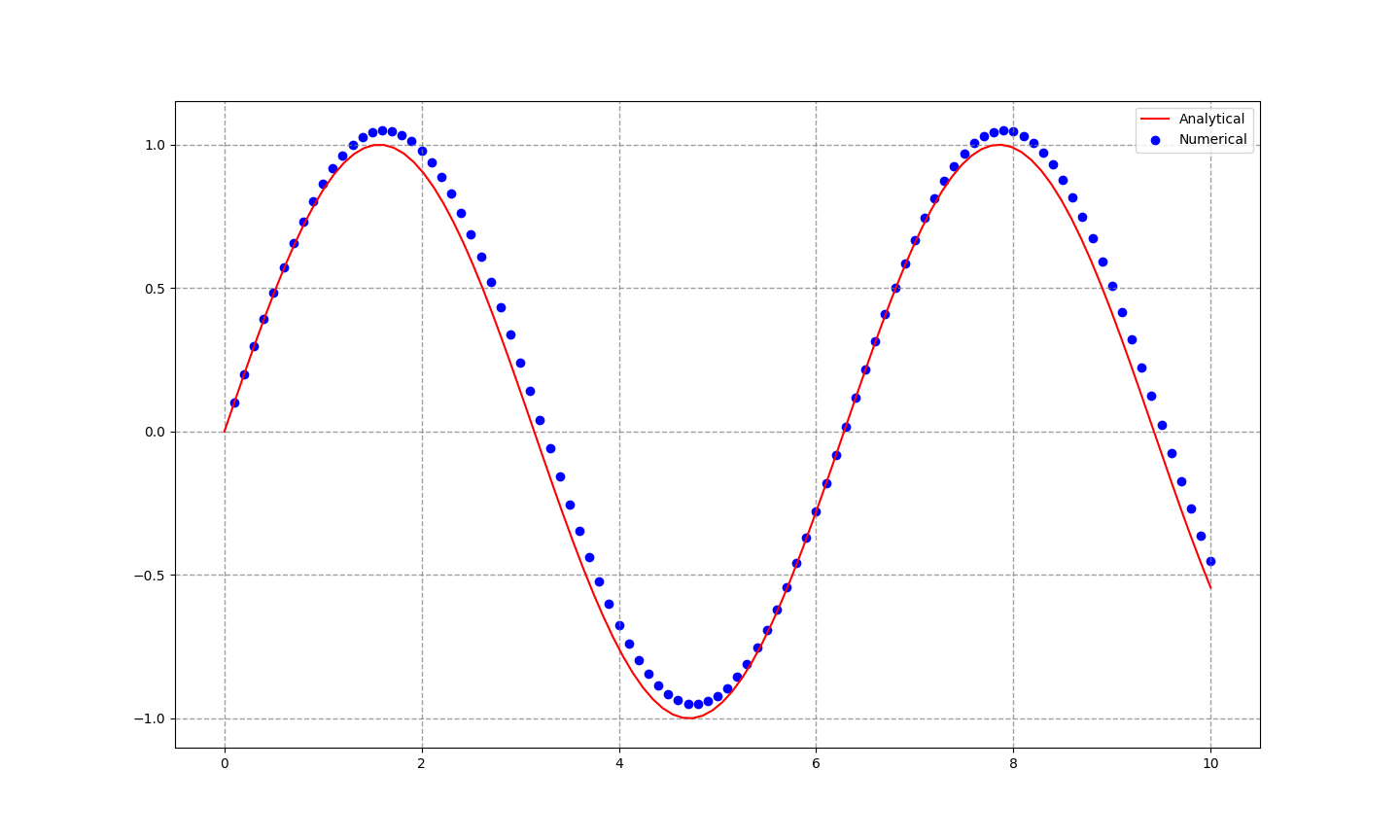
10倍の荒さで計算してみました。少し、解析解の値からずれてしまいました。このように刻み幅が荒すぎると期待する近似ができなくなってしまいます。
さらに10倍荒くしてみます。
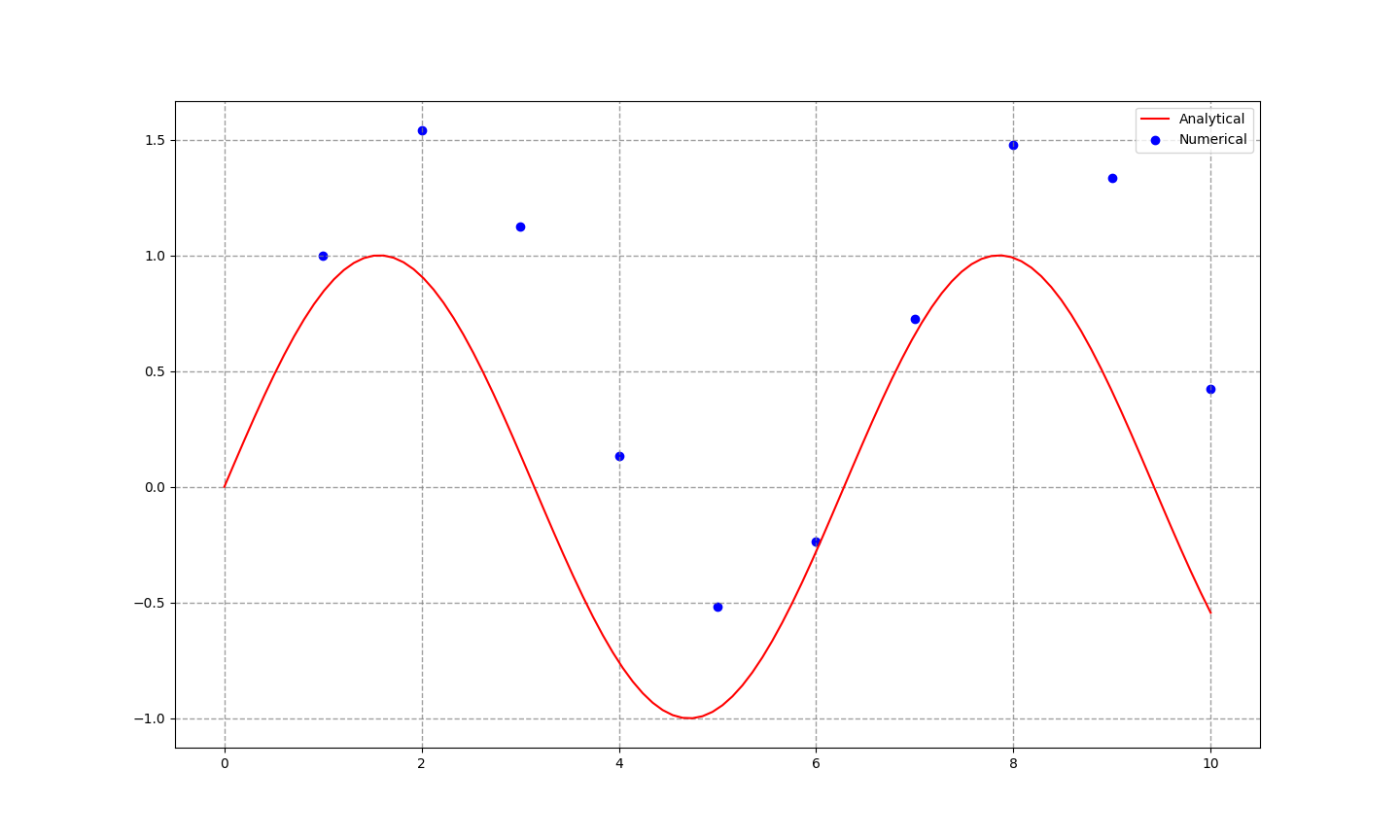
もう、全然期待する結果を得られなくなってしまいました。
さて、差分法について少し理解していただけたかと思います。次にもう少し複雑な微分方程式に用いてみましょう。
4次ルンゲ=クッタ法によるSEIRモデルの計算
SEIRモデルは感染症流行の数理モデルの一種です。インフルエンザやコロナウイルスなどのウイルスの感染を表現することができます。
(注)これはあくまでモデルであり、完全な予測ではありません。定性的に再現できているだけです。
- 免疫を持たない者 (Susceptible)
- 感染症が潜伏期間中の者 (Exposed)
- 発症者 (Infectious)
- 免疫獲得者 (Recovered)
で構成されたモデルです。
SEIRモデルは以下の4つの微分方程式で表現されます。
\begin{align}
\frac{dS}{dt} &= m (N - S) - bSI\\
\frac{dE}{dt} &= bSI - (m + a)E\\
\frac{dI}{dt} &= aE - (m + g)I\\
\frac{dR}{dt} &= gI - mR\\
\end{align}
$t$は時間、$m$は出生率及び死亡率、$a$は感染症の発症率、$b$は感染症への感染率、$g$は感染症からの回復率です。
このSEIRモデルの微分方程式をみていただくと、それぞれの微分方程式が$S,E,I,R$を相互的に持っており、解析解を導くことが困難です。このような場合に、差分法は力を発揮します。
今回用いる差分法は4次精度のルンゲ=クッタ法を用います。ルンゲ=クッタ法には2次精度のものなどいくつかありますが、4次精度のものが簡単で最もポピュラーです。
ルンゲ=クッタ法について書いていると、めちゃくちゃ長くなっちゃいそうなので今回は省略します。
@kaityo256さんの古典4次Runge-Kutta法の精度確認が非常に丁寧に記述されているので参考にしてみて下さい。
プログラム
import numpy as np
import matplotlib.pyplot as plt
# const
N = 5000
S = N - 10
E = 10
I = 0
R = 0
X = np.array([S, E, I, R])
beta = 0.001 #感染症への感染率
epsilon = 0.06 #感染症の発症率
gamma = 0.1 #感染症からの回復率
mu = 0.001 #出生率及び死亡率
# function
def RungeKutta(t, X):
k_1 = seirEquation(t, X)
k_2 = seirEquation(t + dt/2, X + k_1*dt/2)
k_3 = seirEquation(t + dt/2, X + k_2*dt/2)
k_4 = seirEquation(t + dt, X + k_3*dt)
X_next = X + dt/6*(k_1 + 2*k_2 + 2*k_3 + k_4)
return X_next
def seirEquation(t, X):
s = X[0]
e = X[1]
i = X[2]
r = X[3]
return np.array([-beta*s*i+mu*(N-s),
beta*s*i-(mu+epsilon)*e,
epsilon*e-(mu+gamma)*i,
gamma*i-mu*r
])
# main process
dt = 1
t = 0
t_end = 100
T = np.arange(t, t_end+dt, dt)
data = np.r_[X]
while t < t_end:
X = RungeKutta(t, X)
t += dt
data = np.c_[data, X]
fig = plt.figure()
plt.plot(T[:], data[0,:], label = 'Susceptible')
plt.plot(T[:], data[1,:], label = 'Exposed')
plt.plot(T[:], data[2,:], label = 'Infectious')
plt.plot(T[:], data[3,:], label = 'Recovered')
plt.xlabel(r'time')
plt.ylabel(r'Number of people')
plt.legend()
plt.grid(which = "major", axis = "x", color = "gray", alpha = 0.75, linestyle = "--", linewidth = 1)
plt.grid(which = "major", axis = "y", color = "gray", alpha = 0.75, linestyle = "--", linewidth = 1)
plt.show()
出力結果
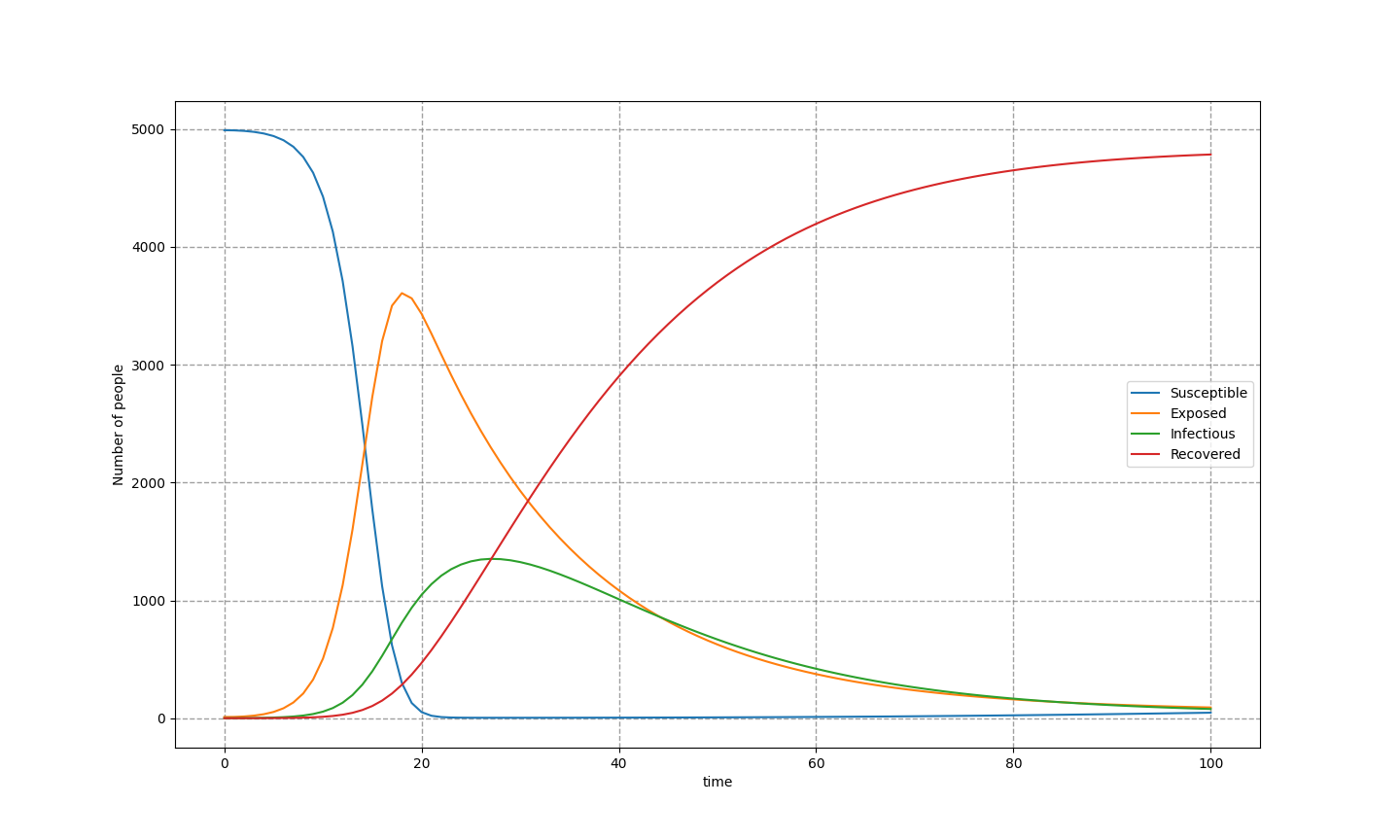
今回は全人口を5000人として、感染症が潜伏期間中の者が10人いるところから計算を開始しました。開始日を0日目として100日目までの感染計算をしました。
beta, epdilon, gamma, muの値やSEIRの初期値を変更することで結果は大きく変わります。カオス的な振る舞いっていうやつです。
終わりに
今回は差分法(オイラー法、ルンゲ=クッタ法)を紹介しました。シミュレーションでよく用いられる手法なので是非勉強してみて下さい。
少しでも興味を持っていただけたら嬉しいです。
明日は、42tokyo Advent calendar 2020の16日目でkotoさんです。 ポケモン対戦環境の歴史についてだそうです。
お楽しみに!!