累積和とは
探索方法の一つ。全探索と比較して計算回数が少ないため、探索にかかるスピードをあげることができる。累積和の名の通り、和を累積していき作成する表を用いる。
Atcoderの実際の過去問及びPythonによる解法を示し、累積和の知見を深める。
問題:ABC122-C - GeT AC
A, C, G, T からなる長さ N の文字列 S が与えられます。以下の
Q 個の問いに答えてください。
問 i (1≤i≤Q): 整数 li,ri (1≤li<ri≤N) が与えられる。S の先頭から li 文字目から ri 文字目までの (両端含む) 部分文字列を考える。この文字列に AC は部分文字列として何回現れるか。
n,q=map(int,input().split())
s=input()
lr=[list(map(int,input().split())) for _ in range(q)]
cnts=[0 for _ in range(n)]
for i in range(1,n):
if (s[i-1],s[i]) == ('A','C'):
cnts[i] = cnts[i-1]+1
else:
cnts[i] = cnts[i-1]
for l,r in lr:
print(cnts[r-1]-cnts[l-1])
問題:ABC037-C - 総和
長さ N の数列 {ai} と1 以上 N 以下の整数 K が与えられます。
この数列には長さ K の連続する部分列が N−K+1 個あります。
これらのそれぞれ部分列に含まれる値の合計の総和を求めてください。
N,K = map(int, input().split())
a = list(map(int, input().split()))
# N,K = 5,3
# a = [1, 2, 4, 8, 16]
# 1.mt:累積和表
mt = [0]
for i, aa in enumerate(a):
mt.append(mt[i] + aa)
#mt=[0, 1, 3, 7, 15, 31]
ans = 0
for i in range(K,N+1):
ans += (mt[i]-mt[i-K])
print(ans)
例としてai=[1, 2, 4, 8, 16]、N=5、K=3、で考える。
今回の例ではfor文を用いて地道に計算するのでもいいが入力値が大きくなるにつれて計算量は増大してしまうので累積を用いて行う。
一般的な解法としては
1.累積和表を用意し、累積和を格納->
2.合計値表を用意し、累積和表から区間合計を格納->
3.合計値表のsumが解となる
となるが今回はmt[i]-mti-Kのsumが解となる。
問題:ABC177C - Sum of product of pairs
N 個の整数 A1,…,AN が与えられます。1≤i<j≤N を満たす全ての組 (i,j) についての Ai×Aj の和を mod(109+7) で求めてください。
N=int(input())
A=list(map(int,input().split()))
# 累積和
rs=[0]*(N+1)
for i in range(1,N+1):
rs[i] = rs[i-1] + A[i-1]
a = 10**9+7
ans=0
for i in range(N-1):
ans+=(A[i]*(rs[-1]-rs[i+1]))
print(ans%a)
問題:ABC172C - Tundoku
二台の机 A, B があります。机 A には N 冊の本が、机 B には M 冊の本が、それぞれ縦に積まれています。机 A に現在上から i 番目に積まれている本 (1≤i≤N) は読むのに Ai 分を要し、机 B に現在上から i 番目に積まれている本 (1≤i≤M) は読むのに Bi 分を要します。次の行為を考えます。
本が残っている机を選び、その机の最も上に積まれた本を読んで机から取り除く。
合計所要時間が K 分を超えないようにこの行為を繰り返すとき、最大で何冊の本を読むことができるでしょうか。本を読むこと以外に要する時間は無視します。
N,M,K = 3,4,1
A=[60,90,120]
B=[80,150,80,150]
ans=0
sum_A=[0]*(N+1)
sum_B=[0]*(M+1)
for i in range(1,N+1):
sum_A[i] = sum_A[i-1] + A[i-1]
for j in range(1,M+1):
sum_B[j] = sum_B[j-1] + B[j-1]
b=M
for a in range(N+1):
if sum_A[a]>K:
break
while sum_B[b] > K-sum_A[a]:
b-=1
ans = max(ans, a+b)
print(ans)
毎回足し算を行うとLTE、累積和を用いてインデックスを利用すれば効率よく探索できる。
ABC134-C - Exception Handling
長さ N の数列 A1,A2,...,AN が与えられます。
1 以上 N 以下の各整数 i に対し、次の問いに答えてください。
数列中の Ai を除く N−1 個の要素のうちの最大の値を求めよ。
N = 3
a = [1,4,3]
# iより左側の場所での最大値、左側の場所での最大値を格納する配列を用意
left_max = [0]*N
right_max = [0]*N
for i in range(1,N):
left_max[i] = max(left_max[i-1],a[i-1])
#[0, 1, 4]
right_max[N-i-1] = max(right_max[N-i],a[N-i])
#[4, 3, 0]
# 2配列の要素ごとで最大値を通れば解
for j in range(N):
print(max(left_max[j], right_max[j]))
ARC098C - Attention
N 人の人が東西方向に一列に並んでいます。 それぞれの人は、東または西を向いています。 誰がどの方向を向いているかは長さ N の文字列 S によって与えられます。 西から i 番目に並んでいる人は、Si= E なら東を、Si= W なら西を向いています。
あなたは、N 人のうち誰か 1 人をリーダーとして任命します。 そして、リーダー以外の全員に、リーダーの方向を向くように命令します。 このとき、リーダーはどちらの方向を向いていても構いません。
並んでいる人は、向く方向を変えるのを嫌っています。 そのためあなたは、向く方向を変える人数が最小になるようにリーダーを選びたいです。 向く方向を変える人数の最小値を求めてください。
N = 12
s = "WEWEWEEEWWWE"
WL_num = [0]*N
ER_num = [0]*N
for i in range(1,N):
if s[i-1] == 'W':
WL_num[i] = WL_num[i-1] + 1
else:
WL_num[i] = WL_num[i-1]
if s[N-i] == 'E':
ER_num[N-i-1] = ER_num[N-i] + 1
else:
ER_num[N-i-1] = ER_num[N-i]
# WL_num:[0, 1, 1, 2, 2, 3, 3, 3, 3, 4, 5, 6]
# ER_num:[6, 5, 5, 4, 4, 3, 2, 1, 1, 1, 1, 0]
ans = float('inf')
for i in range(N):
ans = min(ans, WL_num[i]+ER_num[i])
print(ans)
上の問題+累積和。
ABC125C - GCD on Blackboard
N 個の整数 A1,A2,...,AN が黒板に書かれています。
あなたはこの中から整数を 1 つ選んで、1 以上 109 以下の好きな整数に書き換えます。
元の整数と同じ整数に書き換えても構いません。
書き換えた後の N 個の整数の最大公約数の最大値を求めてください。
import math
N = 3
a = [7,6,8]
# iより左側の集合の最大公約数をlgcd,右側の最大公約数をrgcdに格納
lgcd = [0]*N
lgcd[0]=a[0]
rgcd = [0]*N
rgcd[N-1] = a[N-1]
for i in range(1,N):
lgcd[i] = math.gcd(lgcd[i-1], a[i-1])
rgcd[N-i-1] = math.gcd(rgcd[N-i],a[N-i])
# lgcd=[7, 7, 1]
# rgcd=[2, 8, 8]
ans=0
for i in range(N):
if i == 0:
ans = max(ans,rgcd[i])
elif i == N-1:
ans = max(ans,lgcd[i])
else:
ans = max(ans,math.gcd(lgcd[i],rgcd[i]))
print(ans)
ABC124-D - Handstand
N 人の人が左右一列に並んでいます。0, 1 からなる長さ N の文字列 S と正整数 K が与えられます。
左から i 番目の人は、S の i 文字目が 0 のとき直立し、1 のとき逆立ちしています。
あなたは K 回まで以下の指示を行います。一度も行わなくても構いません。
指示:
1≤l≤r≤N を満たす整数 l,r を選ぶ。左から l,l+1,...,r 番目のの状態を反転する。すなわち、i=l,l+1,...,r について、左から
i 番目の人は直立していれば逆立ちし、逆立ちしていれば直立する。
K 回までの指示で、逆立ちした人を連続で最大何人並ばせることができるか求めてください。
N,K = 6 ,2
s = "110010"
nums = []
cnt_1 = 0
cnt_0 = 0
# ランレングス圧縮 10101...1の形にする
for i in range(N):
if s[i] == '1':
if cnt_0 != 0:
nums.append(cnt_0)
cnt_0 = 0
cnt_1+=1
else:
if cnt_0 == 0:
nums.append(cnt_1)
cnt_1 = 0
cnt_0 += 1
if i==(N-1):
if cnt_0 == 0:
nums.append(cnt_1)
else:
nums.append(cnt_0)
nums.append(0)
# 累計和
ms = [0]*(len(nums)+1)
for j in range(1,len(nums)+1):
ms[j] = ms[j-1] + nums[j-1]
# ms=[0, 0, 3, 4, 5]
# print(ms)
ans=0
# for文が動くようにKの整理
while (len(ms)-2*K-1)<0:
K-=1
for k in range(0,len(ms)-2*K-1,2):
ans = max(ans,ms[k+2*K+1]-ms[k])
print(ans)
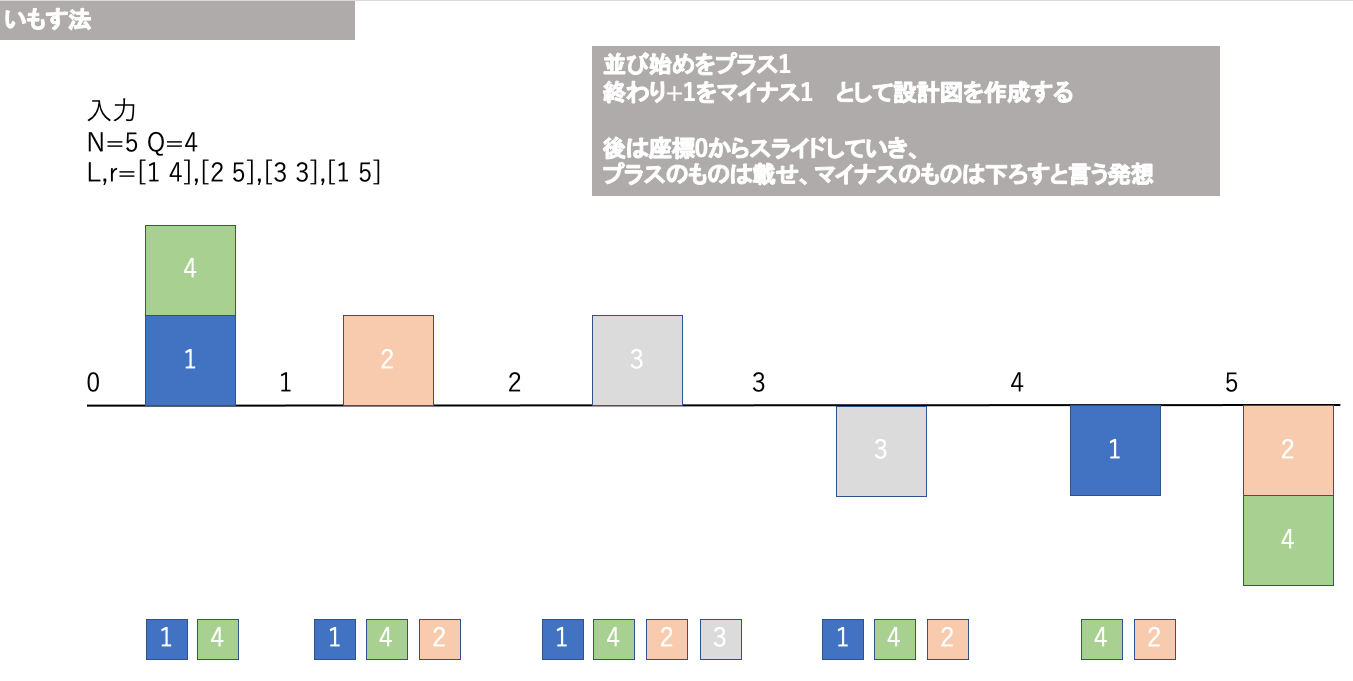
いもす法
累積和の発想を多次元に派生したもの.
問題ABC035C - オセロ
黒の面に0、白の面に1が書かれた N 個のオセロの駒が、どの駒も黒の面が上を向くように一列に並べられています。その後、ある区間にある駒を全て裏返すという操作が Q 回だけ行なわれました。 具体的には i 回目の操作においては、左から li 番目の駒から ri 番目の駒までの駒全てが裏返されました。
最終的な盤面を求めてください。
n,q=map(int,input().split())
lr= [list(map(int,input().split())) for _ in range(q)]
ans=[""]*n
# スライドさせる設計図
imosu=[0]*(n+1)
# 設計図作成
for l,r in lr:
imosu[l-1]+=1
imosu[r]-=1
now=0
# スライドさせていく
for i in range(n):
now+=imosu[i]
ans[i] = str(now%2)
print(*ans, sep="")
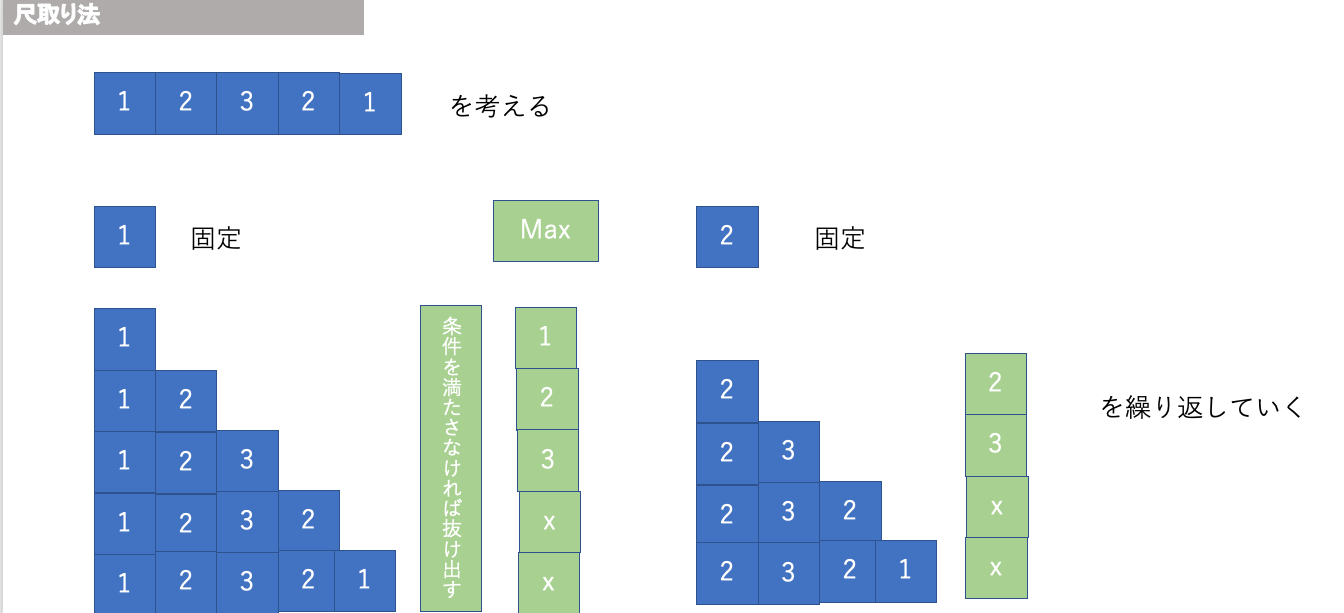
尺取り法
全探索でO(n^2)->O(n)にできる手法.
条件のうち最大値を見つけたり、条件に当てはまるものを数え上げる問題に使える.
ABC038C - 単調増加
N 個の数からなる数列が与えられます。i番目の数をaiと呼びましょう。
al,al+1,...,ar が単調増加、すなわち l≦r であって ai<ai+1 がl≦i<r を満たす全てのiに対して成り立つような
(l,r)の数を求めてください。
n=int(input())
a=list(map(int,input().split()))
r=0
ans=0
for l in range(n):
while r<n-1 and a[r] < a[r+1]:
r+=1
ans+=(r-l+1)
if r==l:
r+=1
print(ans)