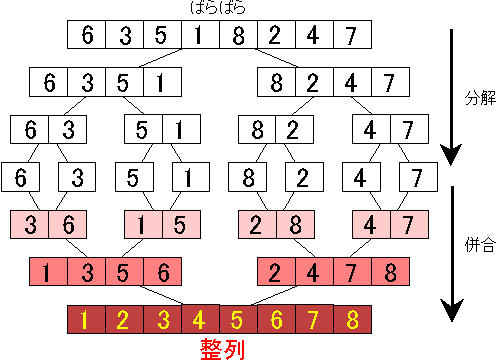
マージソートとは?
ソートの一種。安定したソート。分割統治法(divide-and-conquer)を使用している。
- ソート対象の配列を2分割する(divide)
- 分割したものをさらに2分割するのを要素が1つになるまで繰り返す(divide)
- それぞれの先頭要素同士を比較して、小さい数値を前方にしてマージ(solve, merge)
- ソート済み同士の要素の最初の数値を比較して小さい方から並べてマージ(conquer, merge)
参考:鹿児島大学HP
## マージソートのコード
# 最少単位に分解後にmergeを行う。この処理を繰り返す
def merge_sort(arr):
#要素が1つか0のときはその配列をそのまま返す。(比較対象がなくソートの必要性がないため)
if len(arr) <= 1:
return arr
#2分割する。スライスで切り分けるため、整数部のみ抽出する
mid = len(arr)//2
#元の配列を2分割
arr1 = arr[:mid]
arr2 = arr[mid:]
#最少単位になるまで2分割を続ける
#returnになった時点で再帰が終了する
arr1 = merge_sort(arr1)
arr2 = merge_sort(arr2)
return merge1(arr1, arr2)
# 2つの要素を比較して、小さい方を先頭に並べる
def merge1(arr1,arr2):
#マージ結果を入れる配列
merged = []
l_i, r_i =0,0
while l_i < len(arr1) and r_i < len(arr2):
if arr1[l_i] <= arr2[r_i]:
merged.append(arr1[l_i])
l_i += 1
else:
merged.append(arr2[r_i])
r_i += 1
if l_i < len(arr1):
merged.extend(arr1[l_i:])
if r_i < len(arr2):
merged.extend(arr2[r_i:])
return merged
確認
list=[7,4,3,5,6,1,2]
merge_sort(list)
# [1, 2, 3, 4, 5, 6, 7]
## マージソートの詳細 2つの関数が走っているためわかりにくいので分解してみる。
- 最少単位を作る関数(div_arr)
- 比較して小さい方を配列に追加していく関数(merge)
最少単位を作る関数
まずは、各要素を全て分割する関数を考える
def div_arr(arr):
#要素が1つか0のときはその配列をそのまま返す。(比較対象がなくソートの必要性がないため)
if len(arr) <= 1:
return print(arr)
#2分割する。スライスで切り分けるため、整数部のみ抽出する
mid = len(arr)//2
#元の配列を2分割
arr1 = arr[:mid]
arr2 = arr[mid:]
#最少単位になるまで2分割を続ける
#returnになった時点で再帰が終了する
arr1 = div_arr(arr1)
arr2 = div_arr(arr2)
確認
list=[7,4,3,5,6,1,2]
div_arr(list)
[7]
[4]
[3]
[5]
[6]
[1]
[2]
ポイントはarr1とarr2の2つを用意していること。
関数に投入された値は2分割され、後方(arr2)は常に処理がストックされる。
このため、arr1がreturnで終了したあとも、arr2がストックされた分だけ処理され続ける。
return arrで配列が出力されることを想定していたが、何も表示されたないため、return print(arr)にしている。(なぜ表示されないか不明、、)
### (参考)前列だけで再帰処理した場合
def div_arr(arr):
if len(arr) <= 1:
return print(arr)
mid = len(arr)//2
arr1 = arr[:mid]
arr1 = div_arr(arr1)
list=[7,4,3,5,6,1,2]
div_arr(list)
[7]
arr1しか処理しないため、[7]だけが出力される。
※[7],[4],[3]とならない。再帰処理を繰り返す中で、[4],[3]はarr2に割り振られるため。
## 比較して小さい方を配列に追加していく関数
# 2つの要素を比較して、小さい方を先頭に並べる
def merge1(arr1,arr2):
#マージ結果を入れる配列
#初期値0だが、mergeを繰り返す度に中身が増えていく
merged = []
#対比する要素の配列番号初期値
l_i, r_i =0,0
#ループ終了条件。どちらかの配列を全て比較仕切ったら終了
while l_i < len(arr1) and r_i < len(arr2):
#前方の要素の方が小さい場合
#同じ場合は先方を優先するためイコールをつける
if arr1[l_i] <= arr2[r_i]:
merged.append(arr1[l_i])
#同じ要素を再度検証しないよう配列番号に1をたす。
l_i += 1
else:
merged.append(arr2[r_i])
r_i += 1
# while文が終了したら、追加されていない方を丸ごと答えに追加する。
# 各配列は既に昇順にソート済みであるため、そのまま追加している。
if l_i < len(arr1):
merged.extend(arr1[l_i:])
if r_i < len(arr2):
merged.extend(arr2[r_i:])
return merged
確認
a=[2,3]
b=[1,8,9]
merge1(a,b)
# [1, 2, 3, 8, 9]
## 全体の処理の流れを可視化 上記2つの処理を踏まえて、merge_sortの処理を見てみる。
# ソートする配列
arr=[7,4,3,5,6]
# 1回目の処理
arr1=[7,4]
arr2=[3,5,6]
# arr1を再帰
arr1`=[7]
arr2`=[4]
## arr1の解##
merge`=[4,7]
# arr2を再帰
arr1``=[3]
arr2``=[5,6]
# arr2``を再帰
arr1```=[5]
arr2```=[6]
## arr2``の解##
merge``=[5,6]
## arr2の解##
merge```=[3,5,6]
## いよいよarrの解##
merge=[3,4,5,6,7]
## arrの解はarr1とarr2をmergeしたもの
# arr1の解 merge`=[4,7]
# arr2の解 merge```=[3,5,6]
、、ややこしい。最後の3行が肝心
arr1 = merge_sort(arr1)
arr2 = merge_sort(arr2)
return merge1(arr1, arr2)
merge_sortの度にmergedした値(merge1の結果)がarr1とarr2に入る。
それがさらにmergeされていく。
これで最少単位まで分解した要素が再度組み上がる。
これ考えた人すげぇ、、そしてこれを理解している人もすげぇ