レベル
- ニューラルネットワークってなに?ってレベルの人向け(超初心者)
- 主に自分への備忘録も兼ねてます
参考文献
1.ニューラルネットワークの概要(入力〜出力まで)
- 入力層・隠れ層・出力層の3*3のニューラルネットワークを想定
- 図と実際の値があった方がわかりやすいので以下に記載
図1.概念図

図2.リンクと重み
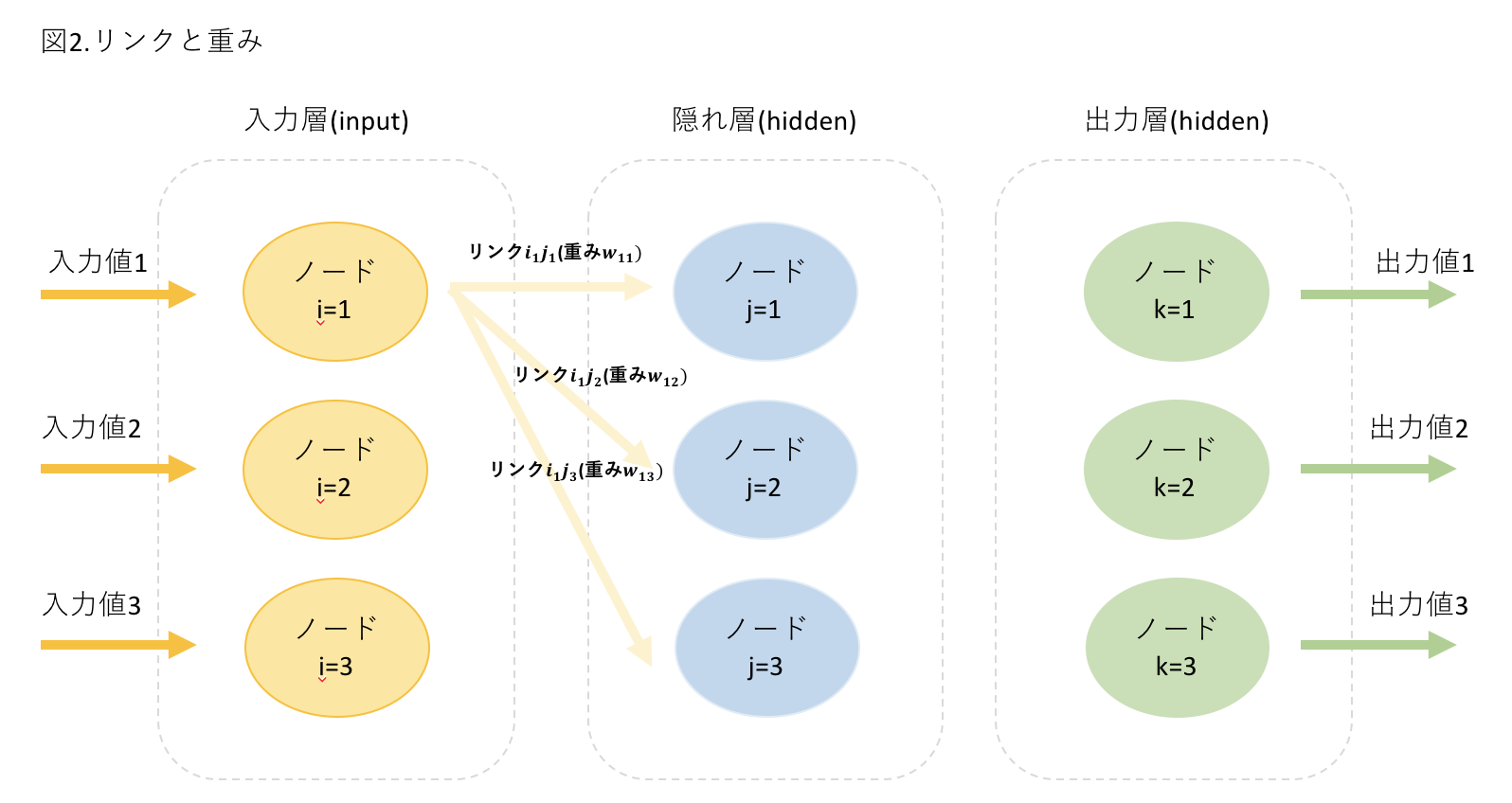
図3.計算方法(入力層への入力から出力層の出力まで)

シグモイド関数と計算方法
そもそも、ニューラルネットワークは動物のニューロンの組織図を模倣して作っている。シグモイド関数は「入力が閾値に達成すると発火する」というニューロンの特性を関数で表現しやすい。
その他の特徴としては、
- ロジスティック関数ともいう
- 計算が他のS字関数よりはるかに簡単
- 0から1の値を「ちょうどよく」出力してくれるのに適している
- 「入力が閾値に達成すると発火する」というニューロンの特性を関数で表現しやすい
シグモイド関数は以下の数式で表します。
y=\frac{1}{1+e^{-x}}
図3の(2)で$O_{hidden}$を計算したい時は、以下の計算を行います。
計算式は、図3の(2)通り、$O_{hidden} = sigmoid(X_{hidden})$である。
X_{hidden}=
\begin{pmatrix}
1.16\\
0.42\\
0.62
\end{pmatrix}\\
となっているので。
O_{hidden} =sigmoid *
\begin{pmatrix}
1.16\\
0.42\\
0.62
\end{pmatrix}\\
例えば、1行1列目を計算するとx=1.16のとき、$e^{-1.16}=0.3135$なので、$y=\frac{1}{1+0.3135}=0.761$となる。
したがって、
O_{hidden} =
\begin{pmatrix}
0.761\\
0.603\\
0.650
\end{pmatrix}
となる。
2.誤差逆伝播と重み更新
誤差逆伝播
1.で導き出した実際の理想値targetsと実際の出力値$O_{output}$には、どうしても誤差が出てしまいます。
理想値に近づけるには重みなどのパラメータを調整する必要があります。ニューラルネットワークでは、最終的な誤差を逆向きに伝送(伝播)していって、重みを更新する、「誤差逆伝播(ごさぎゃくでんぱ)」という手法を用います。概念図を以下に記載します。
ここでは、今まで使っていた33の行列ではなく、話を簡潔にするために23の行列で説明します。
誤差を徐々に前向きに更新していっているのがわかると思います。
エラーの計算
図4の下に記載している数式のように、前のノードのエラーはこのように重みづけwを用いて更新していきます。
ただ、一つ一つ計算するのは大変です。行列の掛け算で実現できないでしょうか?
行列の掛け算による誤差逆伝播の計算
図4のように、最終的な理想値targetsと実際の出力値$O_{output}$の差を誤差$error_{output,1}=0.8$と$error_{output,2}=0.5$ととする。
これを行列で書くとこんな感じの式になる
error_{output} =
\begin{pmatrix}
e_1\\
e_2
\end{pmatrix}
図4の下の計算式を見てもわかる通り、$error_{hidden}$の行列は、上の$error_{output}$を使って、以下の計算で成り立つことがわかります。
error_{hidden} =
\begin{pmatrix}
\frac{w_{11}}{w_{11}+w_{21}} & \frac{w_{12}}{w_{12}+w_{22}} \\
\frac{w_{21}}{w_{21}+w_{11}} & \frac{w_{22}}{w_{22}+w_{12}}
\end{pmatrix}
*
\begin{pmatrix}
e_1\\
e_2
\end{pmatrix}
最も重要な部分はリンクの重み$w_{ij}$と出力誤差$e_n$との掛け算です。重みが大きいほどより多くの出力誤差が隠れ層に渡されます。ここが重要です。
思い切って行列の分母を省いてしまいます。
そうすると、以下のようなシンプルな式になります。
error_{hidden} =
\begin{pmatrix}
w_{11}&w_{12}\\
w_{21}&w_{22}
\end{pmatrix}
*
\begin{pmatrix}
e_1\\
e_2
\end{pmatrix}
行列の左の項は、出力値をだしたときの重みの計算($O=W*I$)の時の$W$の行列
\begin{pmatrix}
w_{11}&w_{21}\\
w_{12}&w_{22}
\end{pmatrix}
の並び順を変えたものです。これを転置行列と言います。$W^T$と書きます。
以上のことを以下の表現で表します。これで誤差逆伝播の誤差の計算は求められました。
$error_{hidden}=W^T_{hidden-output} * error_{output}$
なぜ分母を削除して良いかはおいおい勉強します。。
重みの更新
逆伝播した各層の誤差がこれで計算できたので、この誤差を用いて、いよいよ重みを修正します。
最終的な重みの更新の行列式は以下です。隠れ層と出力層を例にしています。同じことを入力層と隠れ層にも適用しますので、まずは隠れ層と出力層だけ考えます。
誤差は微分をとって傾きを計算し、最小値を求めます。
\Delta W_{jk} = 学習率\alpha * E_k * O_k(1-O_k) * O^T_j$
一つ一つ見ていきます。
$\Delta W_{jk}$は隠れ層のノードjと出力層のノードkの重みの変化率です。これが知りたい値です。
$\alpha$は学習率です。これは定数です。ここまでは簡単。
問題は「$E_k * O_k(1-O_k) * O^T_j$」この式です。
整理します。
- 知りたいのは、重み$W_{jk}$を変化させると、誤差$E$はどのように変化するかということ
- 誤差$E$が最小値をとれば、当然誤算がなくなるので理想値に近づく
- 誤差$E$を重み$W_{jk}$で微分してあげれば、傾きを求められるので、最小値が求められる。
よって、知りたいのは以下の式です。理想値targetを$t_k$ 出力値を$o_k$としています
\frac{\delta E}{\delta W_{jk}} = \frac{\delta (t_k - o_k)^2}{\delta W_{jk}}
そのままだと微分するのが大変なので、合成関数(連鎖律)を使います。
- 連鎖律
\frac{\delta y}{\delta x} = \frac{\delta y}{\delta u} * \frac{\delta u}{\delta x}
ここでは以下のような式になります。
\frac{\delta E}{\delta W_{jk}} = \frac{\delta E}{\delta o_k} * \frac{\delta o_k}{\delta W_{jk}}
一つ目の項を変形します。
$\delta (t_k - o_k)^2$を微分すると$-2 (t_k - o_k)$になります。なぜマイナスが付いているかというと、「正の勾配を持つときは重みを減少させたい、負の勾配を持つときは重みを増加させたい」からです。
二つ目の項も変形します。
図(3)で見た通り、出力値を出したいときはシグモイド関数を使いました。計算式は、図3の(2)通り、$O_{hidden} = sigmoid(X_{hidden})$です。$o_k$にこのシグモイド関数を使った式を代入します。
\frac{\delta o_k}{\delta W_{jk}}=\frac{\delta * sigmoido(\sum_j W_{jk}*o_j)}{\delta W_{jk}}
ここでいう$o_j$は隠れ層の出力なので図3の$O_{hidden}$と同義です。
シグモイド関数を微分することは至難の技なので、既知の公式を用います。
- シグモイド関数の微分の公式
\frac{\delta * sigmoido(x)}{\delta x} = sigmoid(x)( 1-sigmoid(x))
これを使うと、
\frac{\delta E}{\delta W_{jk}}= -2 (t_k - o_k) * sigmoid(\sum_j W_{jk}*o_j)( 1-sigmoid(\sum_j W_{jk}*o_j)) * \frac{\delta (\sum_j W_{jk}*o_j)}{\delta W_{jk}}
となります。
最後の$\frac{\delta (\sum_j W_{jk}*o_j)}{\delta W_{jk}}$はsigmoid関数の中にある式をもう一度合成関数を使っているため、この項が出てきます。ただ、これは計算すると$o_j$と同じのため、以下の式に修正します。ついでに、-2も取り除きます。係数は2だろうが100だろうが微分では消えてしまうため、不要だからです。
まとめると以下の式になります。
\frac{\delta E}{\delta W_{jk}}= -(t_k - o_k) * sigmoid(\sum_j W_{jk}*o_j)( 1-sigmoid(\sum_j W_{jk}*o_j)) * o_j
日本語に直すと、
隠れ層jと出力層kの間の重み($W$) = 出力層kの誤差($E_{output}$)の微分 * 隠れ層jの出力値($O_{hidden}$)
これに学習率を戻してあげると、最終的な式は以下になります。
- 誤差を重みに適用する計算式
\Delta W_{jk} = 学習率\alpha * E_k * O_k(1-O_k) * O^T_j
3.pythonのコードに落とし込む
前置きがだいぶ長くなりましたが、pythonのコードに落とすとこんな感じです。
import numpy
import scipy.special #シグモイド関数expit()使用のため
# ニューラルネットワーククラスの定義
class neuralNetwork:
# ニューラルネットワークの初期化
def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
# 入力層 隠れ層 出力層のノード数の設定
self.inodes = inputnodes
self.hnodes = hiddennodes
self.onodes = outputnodes
# リンクの重み3*3の行列を作る
#input-hiddenのweight(wih) と hidden-outputのweight(who)の2種類
# 行列内の重み weight_ノードi_ノードjへのリンクの重み
# 重みの値は、0.0を平均としてリンクの数の平方根の逆数の範囲にする。pow(self.hnodes, -0.5)はself.hnodesを-1/2乗(power)している(つまり平方根の逆数を取る計算)
# numpy.random.normal(loc(平均) = 0.0、scale(範囲) = 1.0、size = None(例えば(2,3)なら2行3列の行列を作る) )
# w11 w21
# w12 w22 など
self.wih = numpy.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes))
self.who = numpy.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes))
# 学習率の設定
self.lr = learningrate
# 活性化関数(シグモイド関数)の定義
self.activation_function = lambda x: scipy.special.expit(x)
pass
# ニューラルネットワークの学習
def train():
#---------------------------------入力値と出力値の計算--------------------------------------------------------------
# 入力リストを行列に変換(.Tは.transpose()と一緒で転置行列を表す)
#入力は横並びのリストに入れるので、それを縦に並べる処理
# 例:
# input=> a = ([1.0, 0.5, -1.5])
# input=> b = numpy.array(a, ndmin=2).T
# input=> b
# output=> array([[ 1. ],
# output=> [ 0.5],
# output=> [-1.5]])
# numpy.array(object, dtype=None, copy=True, order='K', subok=False, ndmin=0)
# ndminは結果の配列に必要な最小次元数を指定します。この要件を満たすために、必要に応じて形状にあらかじめペンディングされます。
inputs = numpy.array(inputs_list, ndmin=2).T
targets = numpy.array(targets_list, ndmin=2).T #targetsは目標出力
# 隠れ層に入ってくる信号の計算
# 重みとinputの行列を計算して出力値をだす
#numpy.dot(a, b, out = None)
# aは左からかける行列 bは右からかける行列
hidden_inputs = numpy.dot(self.wih,inputs)
# 隠れ層で結合された信号を活性化関数により出力
hidden_outputs = self.activation_function(hidden_inputs)
# 出力層に入ってくる信号の計算
final_inputs = numpy.dot(self.who,hidden_outputs)
# 出力層で結合された信号を活性化関数により出力
final_outputs = self.activation_function(final_inputs)
#---------------------------------誤差逆伝播の計算--------------------------------------------------------------
#目標出力(targets) と最終出力(final_outputs)の差分を計算して出力層の誤差を求め、それを使って転置行列をかけると隠れ層の誤差が更新される。
#出力層の誤差 = (目標出力(targets) - 最終出力(final_outputs))
output_errors = targets - final_outputs
#隠れ層の誤差は出力層の誤差をリンクの重みの割合で更新(転置行列をかける)
hidden_errors = numpy.dot(self.who.T, output_errors)
#---------------------------------重みの更新の計算--------------------------------------------------------------
#上で誤差が更新されたら、その誤差を使って重みを更新する
#隠れ層と出力層の間のリンクの重みを更新
self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose(hidden_outputs))
#入力層と隠れ層の間のリンクの重みを更新
self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs))
pass
# ニューラルネットワークへの照会
def query(self, inputs_list):
# 入力リストを行列に変換
inputs = numpy.array(inputs_list, ndmin=2).T
# 隠れ層に入ってくる信号の計算
hidden_inputs = numpy.dot(self.wih,inputs)
# 隠れ層で結合された信号を活性化関数により出力
hidden_outputs = self.activation_function(hidden_inputs)
# 出力層に入ってくる信号の計算
final_inputs = numpy.dot(self.who,hidden_outputs)
# 出力層で結合された信号を活性化関数により出力
final_outputs = self.activation_function(final_inputs)
return final_outputs
pass
パラメータは以下のように設定します。
# 入力層 隠れ層 出力層のノード数
input_nodes = 3
hidden_nodes = 3
output_nodes = 3
# 学習率
learning_rate = 0.3
# ニューラルネットワークのインスタンスの生成
n = neuralNetwork(input_nodes,hidden_nodes,output_nodes,learning_rate)
ここまで。次回は実際にこのコードを動かすところを記載します。

