Go to Qiita Advent Calendar 2024 Top
LoginSignup
4
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@yusuke_s_yusuke(Yusuke Sakai)in立教大学

Pythonで学ぶ直交距離回帰（ODR）：xとyの誤差を考慮した精密な回帰分析

Last updated at Posted at 2024-11-03

はじめに

回帰分析は、幅広い分野でデータ解析の中心的手法として広く利用されています。特に、最小二乗法（OLS: Ordinary Least Squares）は広く用いられていますが、説明変数 $x$ と応答変数 $y$ の両方に測定誤差が含まれる場合、標準的なOLSでは不十分です。この問題を解決するためには、直交距離回帰（ODR: Orthogonal Distance Regression）が有効です。本記事では、ODRの基本的な概念と、PythonライブラリSciPyを用いた実装方法について説明します。

本記事の実装コードはこちらからもご覧いただけます。

OLSとODRの違い

ODRは、標準的なOLSがデータ点の誤差を縦方向（応答変数 $y$ の方向）にのみ考慮するのに対して、説明変数（独立変数 $x$）の誤差も含めて全体の誤差を最小化するアプローチです。これにより、縦方向と横方向の両方に誤差がある場合でも、より高精度な回帰分析が可能になります。

数式による説明

OLSとODRの違いを数式で説明します。以下の図を用いると、これらの違いが分かりやすくなります。

image.png

OLSでは、回帰モデル $y = f(x; \boldsymbol{\beta})$（$\boldsymbol{\beta}$ はパラメータベクトル）において、データ点が$n$個あるとき、縦方向の誤差を次の式で最小化します。

\text{OLS: } \min_{\boldsymbol{\beta}} \sum_{i=1}^{n} \frac{(y_i - f(x_i; \boldsymbol{\beta}))^2}{\sigma_{y_i}^2}

一方、ODRは説明変数 $x$ と応答変数 $y$ の両方に誤差がある場合に適した回帰手法です。ODR では、次の数式に基づき、全体の誤差を最小化します。

\begin{align}
\text{ODR: }& \min_{\boldsymbol{\beta}} \sum_{i=1}^{n} \left\{ \frac{[x_i - (x_i + \Delta x_i)]^2}{\sigma_{x_i}^2} + \frac{[y_i - f(x_i + \Delta x_i; \boldsymbol{\beta})]^2}{\sigma_{y_i}^2} \right\} \\
= &\min_{\boldsymbol{\beta}} \sum_{i=1}^{n} \left\{ \frac{(\Delta x_i)^2}{\sigma_{x_i}^2} + \frac{(\Delta y_i)^2}{\sigma_{y_i}^2} \right\}\\
\end{align}

ここで、$\sigma_{x_i}$ と $\sigma_{y_i}$ は $x$ と $y$ の測定誤差の標準偏差を表します。ODRでは、OLSの基本的な要素も取り入れています。具体的に言えば、誤差を$\sigma_{x_i}^2$や$\sigma_{y_i}^2$で割るという重み付けの考え方は、OLSにおける応答変数$y$の誤差に対する重み付けと同様です。OLSでは、観測データの不確かさを重み付けして回帰を行いますが、ODRはこれを拡張し、$x$と$y$の両方の誤差を考慮して重み付けを行います。このため、ODRは$x$と$y$の誤差の程度をバランスよく評価し、OLSよりも多様な誤差条件に適応した回帰分析が可能になります。

SciPyを使った実装方法

Pythonでは、scipy.odrモジュールを使用してODRを実装できます。ここでは、基本的な実装手順を説明し、実際のコード例を紹介します。

ODRの実装手順は以下の通りです。

  1. モデル関数の定義
  2. データの生成と観測誤差の設定
  3. RealDataクラスを使用してデータを作成
  4. ODRクラスを用いて回帰を実行

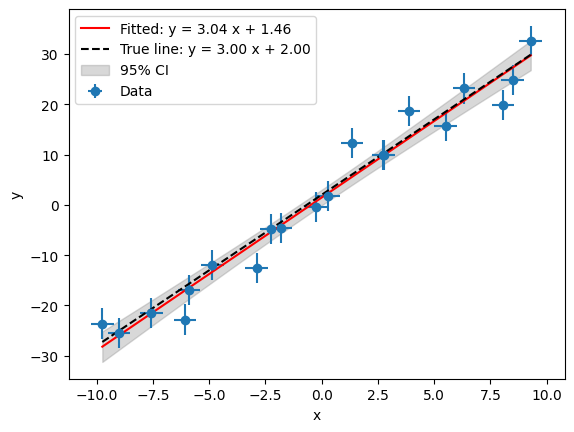
線形回帰モデルの例

まず、線形モデルを使用したODRの実装例を紹介します。 モデルは次のように表されます。

y = f(x; a, b) = ax+b
1次関数モデル
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import ODR, Model, RealData

# 線形モデル
def linear_model(params, x):
    a, b = params
    return a * x + b

# サンプルデータ生成（直線）
np.random.seed(42)
x_true = np.linspace(-10, 10, 20)
params_true = [3.0, 2.0]
y_true = linear_model(params_true, x_true)

# ノイズを加えた観測データ
x_obs = x_true + np.random.normal(0, 0.5, size=x_true.size)
y_obs = y_true + np.random.normal(0, 3.0, size=y_true.size)
x_err = np.full_like(x_obs, 0.5)  # x の誤差
y_err = np.full_like(y_obs, 3.0)  # y の誤差

# ODR 用データとモデルの設定
data = RealData(x_obs, y_obs, sx=x_err, sy=y_err)
model = Model(linear_model)

# ODR 実行
odr_instance = ODR(data, model, beta0=[1.0, 1.0])
output = odr_instance.run()

# フィッティング結果
popt = output.beta
perr = output.sd_beta
print(f"True param: y = {params_true[0]:.2f} x + {params_true[1]:.2f}")
print(f"Fitting result: y = {popt[0]:.2f} x + {popt[1]:.2f}")
print(f"Parameter uncertainty: a_err={perr[0]:.2f}, b_err={perr[1]:.2f}")

# 信頼区間の計算
nstd = 1.96  # 95% 信頼区間
x_fit = np.linspace(x_obs.min(), x_obs.max(), 100)
y_fit = linear_model(popt, x_fit)

# 答えの曲線をプロット
y_true_fit = linear_model(params_true, x_fit)

# 予測区間の計算
y_fit_err = np.sqrt((x_fit**2) * perr[0]**2 + perr[1]**2)
y_fit_up = y_fit + nstd * y_fit_err
y_fit_dw = y_fit - nstd * y_fit_err

# プロット
plt.errorbar(x_obs, y_obs, xerr=x_err, yerr=y_err, fmt='o', label="Data")
plt.plot(x_fit, y_fit, label=f"Fitted: y = {popt[0]:.2f} x + {popt[1]:.2f}", color='r')
plt.plot(x_fit, y_true_fit, label="True line", linestyle='--', color='k')
plt.fill_between(x_fit, y_fit_up, y_fit_dw, color='gray', alpha=0.3, label='95% CI')
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()

出力結果
image.png

コードの説明

  • RealDataクラス: 誤差のある観測データを取り扱うためのクラス。sxとsyで$x$と$y$の誤差を設定します。
  • Modelクラス: 回帰に使用するモデル関数を定義します。
  • ODRクラス: ODRの実行に使用し、初期パラメータbeta0を指定して回帰を行います。

信頼区間は誤差伝搬から計算します。

\begin{align}
\sigma_f &= \sqrt{\left( \frac{\partial f}{\partial a} \sigma_a \right)^2 + \left( \frac{\partial f}{\partial b} \sigma_b \right)^2}\\
&= \sqrt{x^2 \sigma_a^2 + \sigma_b^2}
\end{align}

非線形関数の例

ODRは非線形モデルにも対応しています。ここでは、例として3次関数を用いたODRの実装を紹介します。

線形回帰モデルの例と内容が重複するため折りたたんでいます。必要に応じて開いてご覧ください。 
y = f(x; a, b, c, d) = ax^3 + bx^2 + cx + d
3次間数モデル
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import ODR, Model, RealData

# 3次関数モデル
def cubic_model(params, x):
    a, b, c, d = params
    return a * x**3 + b * x**2 + c * x + d

# サンプルデータ生成（3次関数）
np.random.seed(42)
x_true = np.linspace(-10, 10, 20)
params_true = [1.0, -2.0, 3.0, 4.0]
y_true = cubic_model(params_true, x_true)

# ノイズを加えた観測データ
x_obs = x_true + np.random.normal(0, 0.5, size=x_true.size)
y_obs = y_true + np.random.normal(0, 50.0, size=y_true.size)
x_err = np.full_like(x_obs, 0.5)  # x の誤差
y_err = np.full_like(y_obs, 50.0)  # y の誤差

# ODR 用データとモデルの設定
data = RealData(x_obs, y_obs, sx=x_err, sy=y_err)
model = Model(cubic_model)

# ODR 実行
odr_instance = ODR(data, model, beta0=[1.0, -1.0, 1.0, 1.0])
output = odr_instance.run()

# フィッティング結果
popt = output.beta
perr = output.sd_beta
print(f"True param: y = {params_true[0]:.2f} x^3 + {params_true[1]:.2f} x^2 + {params_true[2]:.2f} x + {params_true[3]:.2f}")
print(f"Fitting result: y = {popt[0]:.2f} x^3 + {popt[1]:.2f} x^2 + {popt[2]:.2f} x + {popt[3]:.2f}")
print(f"Parameter uncertainty: a_err={perr[0]:.2f}, b_err={perr[1]:.2f}, c_err={perr[2]:.2f}, d_err={perr[3]:.2f}")

# 信頼区間の計算
nstd = 1.96  # 95% 信頼区間
x_fit = np.linspace(x_obs.min(), x_obs.max(), 100)
y_fit = cubic_model(popt, x_fit)

# 答えの曲線をプロット
y_true_fit = cubic_model(params_true, x_fit)

# 信頼区間の計算
y_fit_err = np.sqrt((x_fit**6) * perr[0]**2 + (x_fit**4) * perr[1]**2 + (x_fit**2) * perr[2]**2 + perr[3]**2)
y_fit_up = y_fit + nstd * y_fit_err
y_fit_dw = y_fit - nstd * y_fit_err

# プロット
plt.errorbar(x_obs, y_obs, xerr=x_err, yerr=y_err, fmt='o', label="Data")
plt.plot(x_fit, y_fit, label=f"Fitted: y = {popt[0]:.2f} x$^3$ + {popt[1]:.2f} x$^2$ + {popt[2]:.2f} x + {popt[3]:.2f}", color='r')
plt.plot(x_fit, y_true_fit, label=f"True curve: y = {popt[0]:.2f} x^3 + {popt[1]:.2f} x^2 + {popt[2]:.2f} x + {popt[3]:.2f}", linestyle='--', color='k')
plt.fill_between(x_fit, y_fit_up, y_fit_dw, color='gray', alpha=0.3, label='95% CI')
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()

出力結果
image.png

先ほどと同様に誤差伝搬の法則により信頼区間を求めます。

\begin{align}
\sigma_f &= \sqrt{\left( \frac{\partial y}{\partial a} \sigma_a \right)^2 + \left( \frac{\partial y}{\partial b} \sigma_b \right)^2 + \left( \frac{\partial y}{\partial c} \sigma_c \right)^2 + \left( \frac{\partial y}{\partial d} \sigma_d \right)^2}\\
&= \sqrt{x^6 \sigma_a^2 + x^4 \sigma_b^2 + x^2 \sigma_c^2 + \sigma_d^2}
\end{align}

陰関数の例

最後に、陰関数を使用した例として円のフィッティングを紹介します。

x^2+y^2-r^2=0
陰関数の例
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import ODR, Model, RealData
from matplotlib.patches import Circle

# 円の陰関数モデル
def circle_model(params, data):
    r = params[0]
    x, y = data
    return (x**2 + y**2) - r**2

# サンプルデータ生成（円）
np.random.seed(42)
theta = np.linspace(0, 2 * np.pi, 60)
r_true = 5.0
x_true = r_true * np.cos(theta)
y_true = r_true * np.sin(theta)

# ノイズを加えた観測データ
x_obs = x_true + np.random.normal(0, 0.5, size=x_true.size)
y_obs = y_true + np.random.normal(0, 0.5, size=y_true.size)
x_err = np.full_like(x_obs, 0.5)  # x の誤差
y_err = np.full_like(y_obs, 0.5)  # y の誤差

# ODR 用データとモデルの設定
data = RealData(x=np.array([x_obs, y_obs]), y=1, sx=np.array([x_err, y_err]))
model = Model(circle_model, implicit=True)

# ODR 実行
odr_instance = ODR(data, model, beta0=[4.0])
output = odr_instance.run()

# フィッティング結果
r_fit = output.beta[0]
r_err = output.sd_beta[0]
print(f"True param: y = (x^2 + y^2) = {r_true:.2f}^2")
print(f"Fitting result: (x^2 + y^2) = {r_fit:.2f}^2")
print(f"Parameter uncertainty: r_err = {r_err:.2f}")

# 信頼区間の計算
nstd = 1.96  # 95% 信頼区間
r_fit_up = r_fit + nstd * r_err
r_fit_dw = r_fit - nstd * r_err

# フィッティング円と信頼区間のプロット
fig, ax = plt.subplots(subplot_kw={'aspect': 'equal'})
plt.errorbar(x_obs, y_obs, xerr=x_err, yerr=y_err, fmt='o', label="Data")

# フィッティング円のパッチを追加
fitted_circle = Circle(
    (0, 0), r_fit,
    edgecolor='red',
    facecolor='none',
    label=f"Fitted: r={r_fit:.2f}"
)
ax.add_patch(fitted_circle)

# 信頼区間のドーナツ状の塗りつぶし
circle_outer = plt.Circle((0, 0), r_fit_up, color='gray', alpha=0.3, label="95% CI")
circle_inner = plt.Circle((0, 0), r_fit_dw, color='white', alpha=1.0)
ax.add_artist(circle_outer)
ax.add_artist(circle_inner)

# 真の円のパッチを追加
true_circle = Circle(
    (0, 0), r_true,
    edgecolor='k',
    facecolor='none',
    linestyle='--',
    label=f"True circle: r={r_true:.2f}"
)
ax.add_patch(true_circle)

plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.axis("equal")
plt.title("95% confidence interval")
plt.show()

出力結果
image.png

コードの説明

  • RealDataクラス: x=np.array([x_obs, y_obs])、sx=np.array([x_err, y_err])のように、$x$と$y$の情報をxやsxに入れることがポイントです。また、y=1と指定する理由は戻り値の次元に関係しますが、少し複雑なので詳細は公式ページをご参照ください。

    yについて公式ページより If y is an integer, then the Data instance can only be used to fit with implicit models where the dimensionality of the response is equal to the specified value of y.

  • Modelクラス: 陰関数を使う場合は、implicit=Trueと指定します。

まとめ

本記事では、直交距離回帰（ODR）の手法とPythonによる実装方法について解説しました。この手法は、$x$および$y$の両方に誤差が含まれる回帰分析において特に有効です。Pythonのscipy.odrモジュールを使用すれば、線形モデル、非線形モデル、さらには陰関数モデルの実装も簡単に行えます。ぜひ試してみてください。

4
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?