もう迷わない！X線天文学のためのkeV-Å変換と可視化の手引き

はじめに

X線天文学では、エネルギー（keV）と波長（Ångström）の単位変換が欠かせません。論文中の図表を読み解いたり、観測データを解析したりする際に頻繁に必要となるためです。本記事では、PythonとMatplotlibを活用し、この変換を視覚化して直感的に理解できるツールを紹介します。

なお、本記事ではエネルギーを線形スケールで表示する実装に焦点を当てています。

エネルギーと波長の変換

エネルギーと波長は、次の式で表されます。

\lambda (\text{Å}) = \frac{12.398}{E (\text{keV})}

この式を用いると、エネルギー（keV）または波長（Å）のいずれかが分かれば、もう一方を即座に計算できます。ここで、波長の単位「Å（オングストローム）」は、$1~\text{Å} = 10^{-10}~\textrm{m}$（メートル）を意味し、X線天文学では波長を表す一般的な単位です。

この変換式における定数「12.398」は、以下の関係式から導かれます。

E = \frac{hc}{\lambda}

ここで、プランク定数$h$、光速$c$、およびkeVをジュールに変換する定数を用い、単位をオングストロームに合わせることで得られたものです。

実装コードの特徴

本記事の実装コードは、Google Colabからもご覧いただけます。

このツールは、以下の2つの主要な機能を備えています。

1. keVとÅの相互変換

エネルギー（keV）から波長（Å）への変換、およびその逆変換をPythonで簡単に実行できます。直感的な操作で変換を行うことが可能です。

2. 2軸のグラフ作成

Matplotlibを用いて、エネルギー（keV）と波長（Å）を同一グラフ内に同時表示します。これにより、異なる単位でのデータを視覚的に比較できます。

実装コードとグラフの出力例

以下に実装コードとグラフの出力例を示します。

keVを主軸とするグラフ

keVを主軸とする実装コード

keVを主軸とする実装コード

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import FixedLocator

# 波長変換関数
def keV_to_angstrom(keV):
    return 12.398 / (keV + 1e-12)

def angstrom_to_keV(angstrom):
    return 12.398 / (angstrom + 1e-12)

# keV主体のグラフ作成関数
def plot_keV_angstrom_with_wave(keV_range=(1, 10), keV_major_step=1.0, show_wave=True):
    keV = np.linspace(keV_range[0], keV_range[1], 1000)  # keV範囲を設定
    angstrom = keV_to_angstrom(keV)  # 対応するÅを計算

    fig, ax1 = plt.subplots(figsize=(10, 3))

    # サインカーブ (Å基準、10山)
    if show_wave:
        wave_period = (angstrom[-1] - angstrom[0]) / 10
        wave = np.sin(2 * np.pi * (angstrom - angstrom[0]) / wave_period)
        ax1.plot(keV, wave, label="Wave (based on Å)")
        ax1.legend()

    # メインx軸 (keV)
    ax1.set_xlabel("Energy (keV)")
    ax1.set_ylabel("Amplitude" if show_wave else "")
    ax1.set_xlim(keV_range[0], keV_range[1])  # keV範囲

    # 主目盛りの位置を計算
    keV_major_ticks = np.arange(keV_range[0], keV_range[1] + keV_major_step, keV_major_step)
    ax1.xaxis.set_major_locator(FixedLocator(keV_major_ticks))
    ax1.grid(visible=True, linestyle="--", linewidth=0.5, alpha=0.7)  # グリッド設定

    # 副x軸 (Å)
    ax2 = ax1.secondary_xaxis("top", functions=(keV_to_angstrom, angstrom_to_keV))
    ax2.set_xlabel("Wavelength (Å)")
    angstrom_major_ticks = keV_to_angstrom(keV_major_ticks)
    ax2.set_xticks(angstrom_major_ticks)
    ax2.set_xticklabels([f"{x:.2f}" for x in angstrom_major_ticks])  # 目盛りラベル

    plt.title("Energy-Wavelength Dual Axis with Optional Wave")
    plt.tight_layout()
    plt.show()

# 実行例
plot_keV_angstrom_with_wave(
    keV_range=(1, 20),  # keVの範囲
    keV_major_step=1.0, # 主目盛りステップ
    show_wave=True      # 波を描画するか
)

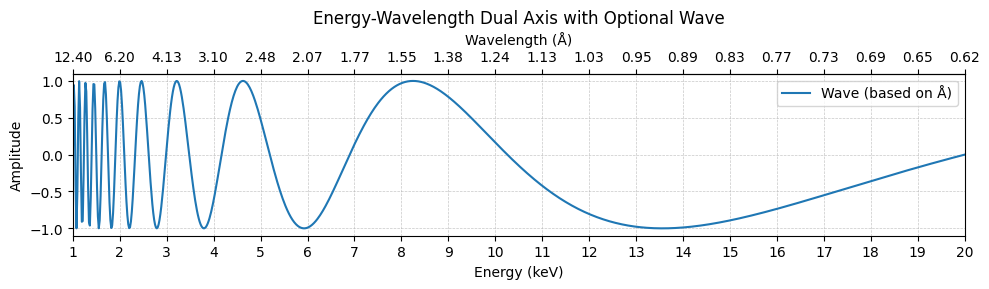
エネルギーを主軸とし、その範囲に対応する波長を副軸として表示したグラフです。波長に基づいたサインカーブを描画することで、エネルギーと波動特性の関係を視覚化しています。

• keV範囲：1～20
• 主目盛り間隔：1 keV

グラフ例：

Åを主軸とするグラフ

Åを主軸とする実装コード

Åを主軸とする実装コード

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import FixedLocator

# 波長変換関数
def keV_to_angstrom(keV):
    return 12.398 / (keV + 1e-12)

def angstrom_to_keV(angstrom):
    return 12.398 / (angstrom + 1e-12)

# Å主体のグラフ作成関数
def plot_angstrom_keV_with_wave(angstrom_range=(1.24, 12.4), angstrom_major_step=1.0, show_wave=True):
    angstrom = np.linspace(angstrom_range[0], angstrom_range[1], 1000)  # Å範囲を設定
    keV = angstrom_to_keV(angstrom)  # 対応するkeVを計算

    fig, ax1 = plt.subplots(figsize=(10, 3))

    # サインカーブ (keV基準、10山)
    if show_wave:
        wave_period = (keV[-1] - keV[0]) / 10
        wave = np.sin(2 * np.pi * (keV - keV[0]) / wave_period)
        ax1.plot(angstrom, wave, label="Wave (based on keV)")
        ax1.legend()

    # メインx軸 (Å)
    ax1.set_xlabel("Wavelength (Å)")
    ax1.set_ylabel("Amplitude" if show_wave else "")
    ax1.set_xlim(angstrom_range[0], angstrom_range[1])  # Å範囲

    # 主目盛りの位置を計算
    angstrom_major_ticks = np.arange(angstrom_range[0], angstrom_range[1] + angstrom_major_step, angstrom_major_step)
    ax1.xaxis.set_major_locator(FixedLocator(angstrom_major_ticks))
    ax1.grid(visible=True, linestyle="--", linewidth=0.5, alpha=0.7)  # グリッド設定

    # 副x軸 (keV)
    ax2 = ax1.secondary_xaxis("top", functions=(angstrom_to_keV, keV_to_angstrom))
    ax2.set_xlabel("Energy (keV)")
    keV_major_ticks = angstrom_to_keV(angstrom_major_ticks)
    ax2.set_xticks(keV_major_ticks)
    ax2.set_xticklabels([f"{x:.2f}" for x in keV_major_ticks])  # 目盛りラベル

    plt.title("Wavelength-Energy Dual Axis with Optional Wave")
    plt.tight_layout()
    plt.show()

# 実行例
plot_angstrom_keV_with_wave(
    angstrom_range=(1, 25),  # Åの範囲
    angstrom_major_step=1.0,      # 主目盛りステップ
    show_wave=True                # 波を描画するか
)

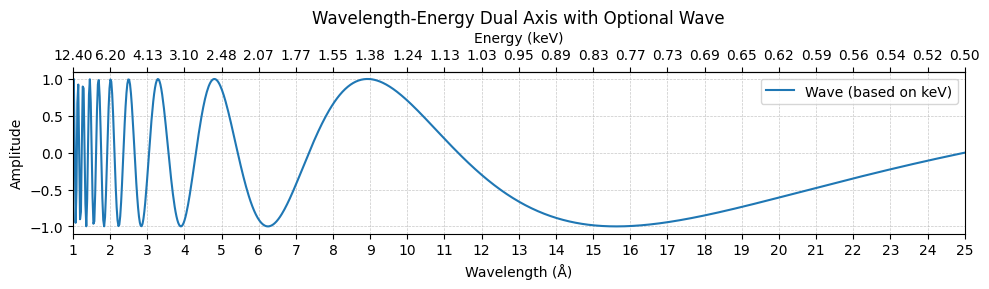
波長を主軸にし、エネルギーを副軸で表示したグラフです。

• Å範囲：1～25
• 主目盛り間隔：1 Å

グラフ例：

実装のポイントと補足

1. 2軸の実装

Matplotlibのsecondary_xaxisを利用し、keVとÅを主軸と副軸で同時に表示しています。この機能により、エネルギーと波長の対応関係を一目で確認することができます。

なお、secondary_xaxisでは内部的に変換式（例：keV_to_angstrom）を使用し、あらゆるスケール変換を解釈して目盛りを自動的に配置する仕組みがあります。このため、ゼロやゼロに近い値が分母に含まれる変換式では、ゼロ割りエラーが発生する可能性があります。これを防ぐために、変換式の分母に1e-12のような小さな値を加える工夫が重要です。こうした補正を行うことで、極端な値や境界値を含むデータでも正確なグラフを生成することができます。

2. 目盛りの調整

主要な目盛り位置をFixedLocatorで手動設定することで、正確な数値ラベルを表示します。これにより、グラフが読み取りやすくなります。

3. サインカーブの描画

波長やエネルギー範囲に基づくサインカーブを10周期分描画し、目盛りの歪みを視覚的に表現しています。解析結果の理解を助ける工夫です。

まとめ

本記事では、エネルギー（keV）と波長（Å）の変換を行うPythonスクリプトを紹介しました。現在の実装ではエネルギーを線形スケールで表示していますが、Xspecの出力結果と比較する際には対数スケールで表示する方が便利な場合もあります。対数スケール表示にも挑戦しましたが、いくつかのバグが解消できなかったため、本記事では線形スケールの実装に絞りました。

このツールが、X線天文学におけるデータ解析やエネルギーと波長の関係を理解する一助となれば幸いです。