はじめに
この記事では、XSPEC で利用される zashift と vashift モデルの違いを、相対論的および非相対論的ドップラー効果の観点から数式を用いて解説します。特に、相対論的速度での赤方偏移を扱う zashift と、非相対論的速度によるエネルギーシフトを示す vashift が、それぞれエネルギーにどのように影響を与えるかに焦点を当てます。
また、Python を使用して相対論的ドップラーシフトの関係を視覚化し、理論をより深く理解できるようにします。最後に、SS 433 という天体の観測結果を取り上げ、理論と実際の観測データがどのように一致するかを示します。
光のドップラー効果とは
天文学において光のドップラー効果は、運動する天体が放射する光の周波数やエネルギーが、観測者に対してどのように変化するかを説明する重要な現象です。天体から放射された光が観測者に届く際、周波数が増加することを青方偏移、その反対に周波数が減少することを赤方偏移と呼びます。音のドップラー効果と異なり、視線と垂直方向に運動する天体から届く光が赤方偏移する横ドップラー効果や、光行差など、古典的なドップラー効果とは異なる現象も含まれます。
ドップラーシフトの式
光のドップラー効果は、次の式で表されます。
\nu' = \nu \times \frac{\sqrt{1-(V/c)^2}}{1-V/c\cos\theta}
- $ \nu $: 光源から見た周波数
- $ \nu' $: は観測された周波数
- $ V $: 光源の相対速度
- $ c $: 光速
- $ \theta $: 観測者のフレームにおける光源との相対運動の方向に対しての角度
$V$ が小さい場合、テイラー展開を使うことで次のように近似されます。
\nu' = \nu \times \left(1-\frac{V}{c}\cos \theta \right)
これは、非相対論的な近似です。運動する天体が観測者に近づく場合は青方偏移、遠ざかる場合は赤方偏移が起こります。この原理は、次に説明するvashiftモデルにも適用されます。
vashiftとzashiftの違い
vashift(非相対論的ドップラー効果)
XSPECのvashiftモデルは、非相対論的な速度でのエネルギーシフトを次の式で計算します。
E' = E \times \left( 1 - \frac{v}{c} \right)
- $ E $: 静止状態でのエネルギー
- $ E' $: 観測されたエネルギー
- $ v $: 視線方向の速度
この式は、速度が光速に比べて小さい状況で使用されます。
zashift(相対論的ドップラー効果)
zashiftは、相対論的速度にも対応しており、赤方偏移によるエネルギーシフトを次の式で表します。
E' = E \times \frac{1}{(1+z)}
- $ z $: 赤方偏移量。$ z > 0 $ なら赤方偏移、$ z < 0 $ なら青方偏移。
zashiftは、光速に近い天体の運動(相対論的ジェットやクエーサー)に対して使用され、より正確なエネルギーシフトを計算します。速度と赤方偏移の関係は以下の式で与えられます。
1+z={\frac {1-V/c\cos\theta }{\sqrt {1-(V/c)^2}}}
この式により、赤方偏移量$z$から速度$V$を計算できます。
横ドップラー効果
横ドップラー効果とは、視線に垂直な方向に運動する天体が引き起こす赤方偏移現象です。この効果を視覚化するために、異なる速度での赤方偏移量を視線方向の角度$\theta$に対してプロットします。次のPythonコードを用いて、速度が異なる場合の赤方偏移$z$の変化を描画できます。
Pythonによる視線方向の角度とドップラーシフトの描画コード
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.size"] = 14
# プロットのための特定の v/c 値
v_c_values = np.array([0.05, 0.25, 0.45])
# theta 値を生成
theta = np.linspace(0, 180, 100)
theta_rad = np.radians(theta)
# プロット設定
fig, ax = plt.subplots(figsize=(8*1.2, 6*1.2))
for v_c in v_c_values:
# ドップラーシフトに基づく修正された nu' の式
nu_prime = np.sqrt(1 - v_c**2) / (1 - v_c * np.cos(theta_rad))
z = 1 / nu_prime - 1
ax.plot(theta, z, label=rf"$V/c = {v_c:.2f}$")
# 90度の位置に垂直線を追加
ax.axvline(x=90, color='black', linestyle='--')
# 右側に nu'/nu 軸を追加
ax2 = ax.secondary_yaxis('right', functions=(lambda z: 1 / (z + 1), lambda nu_prime: 1 / nu_prime - 1))
ax2.set_ylabel(r'$\nu^\prime / \nu$', rotation=0, labelpad=15)
ax2.set_yticks(np.arange(0.7, 1.7, 0.1))
# 主軸のラベルと範囲を設定
ax.set_xlabel(r'$\theta$ (degrees)')
ax.set_ylabel(r'$z$', rotation=0, labelpad=15)
ax.set_ylim([-0.4, 0.65])
ax.set_yticks(np.arange(-0.4, 0.7, 0.05))
ax.set_xlim([0, 180])
ax.set_xticks(np.arange(0, 181, 10))
# 左軸のグリッドを有効にする
ax.grid(axis='both', color='black', which='major', linestyle='--', linewidth=0.7)
ax.set_title(r'Relativistic Doppler Shift and Redshift for Specific $v/c$ Values')
ax.legend(title="Velocity")
plt.savefig('doppler_shift.png', bbox_inches='tight')
plt.show()
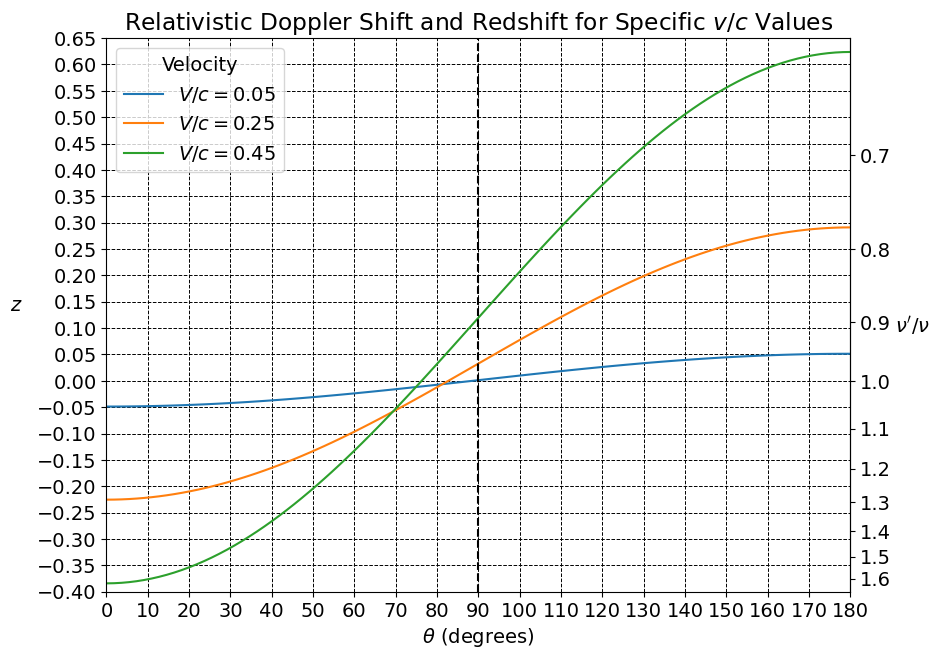
このグラフでは、$V/c=0.05$ では視線に対して垂直な時($\theta=90$度)に赤方偏移がほぼゼロとなる一方で、$V/c=0.25$ や $V/c=0.45$ では赤方偏移が明確に現れることがわかります。これが横ドップラー効果です。
SS 433における横ドップラーシフトの観測
SS 433は、相対論的ジェットを持つ天体として知られており、約 $V/c \approx 0.26$ の速度で、2方向にジェットを放出しています。歳差運動によってジェットの向きが周期的に変化するため、2つのジェットの赤方偏移量 ($z$) が一致する瞬間、視線に対してジェットがほぼ垂直に放射されます。このタイミングで、横ドップラー効果による赤方偏移が観測されます。
(詳しくは手前味噌ですが、SS 433のドップラーシフト解析:Six-ParameterモデルとNodding-Motionモデルの比較 を参照。)
実際、SS 433の観測では、$z \sim 0.03$ の赤方偏移が確認されており、この現象は理論的な予測と一致しています。
下の図は、SS 433のドップラーシフト観測結果を示しており、歳差運動によるジェットの向きの変化が赤方偏移にどのような影響を与えるかがわかります。

まとめ
この記事では、XSPECにおける zashift と vashift モデルの違いを説明しました。
- vashift は、速度が光速に比べて小さい非相対論的な状況で使われます。
- zashift は、光速に近い天体に対して使用され、より広範囲の速度に対応します。
また、SS 433の観測データを通して、横ドップラー効果がどのように現れるかを確認しました。適切なモデルを選択することで、天体の物理的特性をより正確に把握できます。