天体の距離と角度を使って視線垂直距離をPythonで求める方法

Last updated at 2024-09-08Posted at 2024-09-08

はじめに

天文学では、天体の距離や大きさを正確に知ることが重要です。観測によって得られた天体の見かけの大きさ（視直径）と距離から、実際のサイズを計算できます。この手法は、月のように比較的近い天体から、銀河のように非常に遠くにある天体まで、広く使われています。

本記事では、天体の見かけの大きさと距離の関係をもとに、その計算方法をPythonで実装する手順を紹介します。具体例として、月、太陽、超新星残骸カシオペア座A（Cas A）を取り上げ、それぞれの天体のサイズを求める方法を解説します。

角度の単位

天文学では、天体の位置や大きさを表すために、角度を「度（°）」「分（'）」「秒（"）」で表すことが一般的です。

度 (°): 円周の360分の1。
分 ('): 1度の60分の1。
秒 ("): 1分の60分の1（1度の3600分の1）。

これらの単位は天体の見かけの大きさを測る際に使われますが、計算ではラジアンに変換して扱います。

ラジアンは、円の半径と弧の長さの比から定義される角度の単位です。ラジアンを使うことで、角度に関する計算がよりシンプルになります。

天体の見かけの大きさと真の大きさの関係

天体の見かけの大きさ（視直径）とその距離から、天体の真の大きさを求めるための計算式を示します。

角度が与えられたとき天体の視線垂直方向の距離は以下のように与えられます。

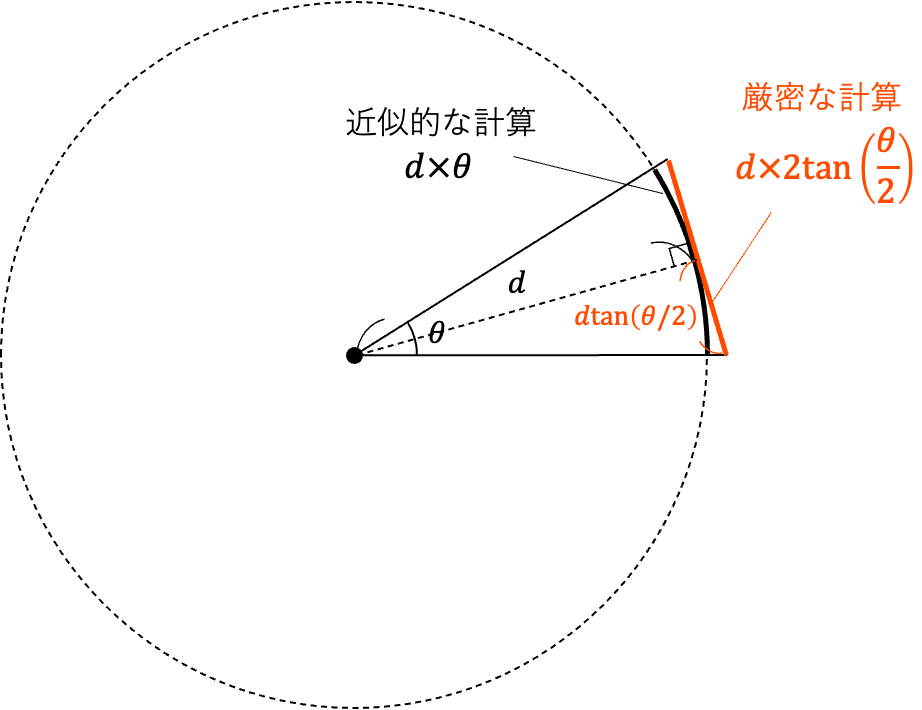
ここで、各変数は次のようになります。

$D$ は天体の真の大きさ（通常はメートルやキロメートル）。
$d$ は天体までの距離（メートル、キロメートル、天文単位、パーセクなど）。
$\theta$ は天体の見かけの角度（ラジアン）。

近似的な計算としては（求める角度が小さい場合）は、

D = d \times \theta

で近似的な計算として十分ですが、より厳密性が求められる場合には

D = d \times 2\tan\left(\frac{\theta}{2}\right)

の式を使います。この記事ではこちらの厳密な方の式を使い実装します。

Pythonによる実装

以下に、天体の見かけの角度（度、分、秒）と距離から、天体の真の大きさを計算するPythonコードを示します。

コードは

こちらからも閲覧できます。

1. 距離と角度の単位変換辞書

まず、距離と角度をSI単位に変換するための辞書を作成します。これにより、異なる単位（天文単位、パーセク、光年など）で与えられた距離をメートルに変換することができます。

import math
from typing import Literal

# 距離単位変換の辞書
DISTANCE_UNITS_TO_METERS = {
    'meter': 1.0,
    'cm': 1e-2,
    'km': 1e3,
    'au': 1.495978707e11,
    'ly': 9.4607304725808e15,
    'pc': 3.085677581491367e+16,
    'kpc': 3.085677581491367e19,
}

# 角度単位変換の辞書（1度あたりのラジアン）
ANGLE_UNITS_TO_RADIANS = {
    'degree': math.radians(1),
    'arcmin': math.radians(1 / 60),
    'arcsec': math.radians(1 / 3600),
}

2. 距離単位の変換関数

異なる単位の距離をメートルに変換する関数を実装します。この関数を使えば、距離が異なる単位で与えられても、メートル単位に統一して計算ができます。

def convert_distance(
    d: float, 
    from_unit: Literal['meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc'], 
    to_unit: Literal['meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc']
) -> float:
    """
    任意の距離単位間で距離を変換する関数

    :param d: 距離の値
    :param from_unit: 元の距離単位
    :param to_unit: 変換後の距離単位
    :return: 変換後の距離
    """
    # 距離をメートルに変換
    d_in_meters = d * DISTANCE_UNITS_TO_METERS[from_unit]
    
    # 目的の単位に変換して返す
    return d_in_meters / DISTANCE_UNITS_TO_METERS[to_unit]

3. 視線垂直方向の距離を計算する関数

角度と距離を使って、天体の真の大きさを計算する関数を実装します。角度は、度・分・秒で入力されますが、計算はラジアンに変換して行われます。

def perpendicular_distance(
    d: float, 
    theta_unit: Literal['degree', 'arcmin', 'arcsec'] = 'arcmin', 
    input_distance_unit: Literal['meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc'] = 'pc', 
    output_distance_unit: Literal['meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc'] = 'pc'
) -> float:
    """
    視線垂直方向の距離を計算する関数

    :param d: 星までの距離
    :param theta_unit: 視線方向の角度の単位（degree, arcmin, arcsec）
    :param input_distance_unit: 入力距離の単位（'meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc'）
    :param output_distance_unit: 出力距離の単位（'meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc'）
    :return: 視線垂直方向の距離（指定された単位）
    """
    # 入力距離をメートルに変換
    d_meters = convert_distance(d, input_distance_unit, 'meter')

    # 角度をラジアンに変換
    theta_rad = ANGLE_UNITS_TO_RADIANS[theta_unit]

    # 視線垂直方向の距離をメートルで計算
    d_perp_meters = 2 * d_meters * math.tan(theta_rad / 2)

    # 結果を指定された出力単位に変換して返す
    d_perp_converted = convert_distance(d_perp_meters, 'meter', output_distance_unit)
    
    # 計算結果を出力
    print(f"1 {theta_unit} = {d_perp_converted:.6e} {output_distance_unit} (at a distance of {d} {input_distance_unit})")
    
    return d_perp_converted

4. 使用例

月の例

まずは、私たちに最も身近な天体である月の大きさを計算します。月の見かけの角度（視直径）は約31分角 (arcmin) で、月までの距離は約384,400 kmです。このデータをもとに、月の真の大きさを計算してみましょう。

月の大きさ

# 使用例（月）
d = 384400  # 距離
theta_unit = 'arcmin'
input_distance_unit = 'km'
output_distance_unit = 'km'

# 視線垂直方向の距離を計算して出力
d_perp = perpendicular_distance(d, theta_unit, input_distance_unit, output_distance_unit)

# 視直径から大きさを計算
apparent_diameter = 31
print(f"Moon size: {apparent_diameter} {theta_unit} = {apparent_diameter*d_perp:.6e} {output_distance_unit}")

出力結果

1 arcmin = 1.118174e+02 km (at a distance of 384400 km)
Moon size: 31 arcmin = 3.466340e+03 km

d: 天体までの距離（この例は月までの距離を km 単位で指定）
theta_unit: 角度の単位（この例は arcmin を指定）
input_distance_unit: 距離 d の単位（km 単位で入力）
output_distance_unit: 出力される結果の距離単位（この例は km 単位で出力）

結果として、月の大きさは約3,466 kmという値が得られます。この値は、月の実際の直径¹に非常に近い結果となり、観測データと理論計算が一致することが確認できます。

太陽の例

次に、太陽の例を見てみましょう。太陽の見かけの角度は約32分角 (arcmin)、地球からの距離は1天文単位 (AU) です。このデータを使用して、太陽の真の大きさを計算します。

太陽の大きさ

# 使用例（太陽）
d = 1  # 距離
theta_unit = 'arcmin'
input_distance_unit = 'au'
output_distance_unit = 'km'

# 視線垂直方向の距離を計算して出力
d_perp = perpendicular_distance(d, theta_unit, input_distance_unit, output_distance_unit)

# 視直径から大きさを計算
apparent_diameter = 32
print(f"Sun size: {apparent_diameter} {theta_unit} = {apparent_diameter*d_perp:.6e} {output_distance_unit}")

出力結果

1 arcmin = 4.351626e+04 km (at a distance of 1 au)
Sun size: 32 arcmin = 1.392520e+06 km

計算結果から、実際の太陽の直径²とほぼ一致することがわかります。

超新星残骸カシオペア座Aの例

最後に、超新星残骸であるカシオペア座A（Cas A）を例に取り上げて、その大きさを計算してみます。この天体は約300年前に爆発した超新星の残骸で、地球からの距離は約3.4キロパーセク（kpc）、視直径は約5.6分角（arcmin）³とされています。

Cas Aの大きさ

# 使用例（カシオペア座A）
d = 3.4  # 距離
theta_unit = 'arcmin'
input_distance_unit = 'kpc'
output_distance_unit = 'ly'

# 視線垂直方向の距離を計算して出力
d_perp = perpendicular_distance(d, theta_unit, input_distance_unit, output_distance_unit)

# 視直径から大きさを計算
apparent_diameter = 5.6  # 視直径（約5.6分角）
print(f"Cas A size: {apparent_diameter} {theta_unit} = {apparent_diameter*d_perp:.6e} {output_distance_unit}")

出力結果

1 arcmin = 3.225752e+00 ly (at a distance of 3.4 kpc)
Cas A size: 5.6 arcmin = 1.806421e+01 ly

計算結果から、カシオペア座Aの視直径は約18光年にも広がっていることがわかります。つまり、光速で移動したとしても、この残骸の端から端まで到達するのに18年かかるという、非常に広大なスケールを持つ天体です。

この天体の大きさを、Chandra X線天文衛星の観測画像と比較することで、想像を膨らますことができます。下図は、Chandraが捉えたカシオペア座Aの観測画像です。巨大な超新星残骸が広がる様子が視覚的に捉えられており、計算結果と比較して観察できます。

(Chandra X-ray Centerからデータを入手：https://cda.harvard.edu/chaser/)

このように、計算を通じてその壮大なスケールがより具体的に感じられるのではないでしょうか。

まとめ

この記事では、天体の距離と角度を使って視線垂直方向の距離を計算する方法をPythonで紹介しました。月、太陽、カシオペア座Aを例に、天体の見かけの大きさと距離から真の大きさを求める手順を説明しました。Pythonを使うことで、計算を簡単に実装でき、他の天体にも応用可能です。ぜひ、他の天体のデータでも試してみてください。

コード全容

実装コードの全容です。

コード全容

import math
from typing import Literal

# 距離単位変換の辞書
DISTANCE_UNITS_TO_METERS = {
    'meter': 1.0,
    'cm': 1e-2,
    'km': 1e3,
    'au': 1.495978707e11,
    'ly': 9.4607304725808e15,
    'pc': 3.085677581491367e+16,
    'kpc': 3.085677581491367e19,
}

# 角度単位変換の辞書（1度あたりのラジアン）
ANGLE_UNITS_TO_RADIANS = {
    'degree': math.radians(1),
    'arcmin': math.radians(1 / 60),
    'arcsec': math.radians(1 / 3600),
}

def convert_distance(
    d: float, 
    from_unit: Literal['meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc'], 
    to_unit: Literal['meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc']
) -> float:
    """
    任意の距離単位間で距離を変換する関数

    :param d: 距離の値
    :param from_unit: 元の距離単位
    :param to_unit: 変換後の距離単位
    :return: 変換後の距離
    """
    # 距離をメートルに変換
    d_in_meters = d * DISTANCE_UNITS_TO_METERS[from_unit]
    
    # 目的の単位に変換して返す
    return d_in_meters / DISTANCE_UNITS_TO_METERS[to_unit]

def perpendicular_distance(
    d: float, 
    theta_unit: Literal['degree', 'arcmin', 'arcsec'] = 'arcmin', 
    input_distance_unit: Literal['meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc'] = 'pc', 
    output_distance_unit: Literal['meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc'] = 'pc'
) -> float:
    """
    視線垂直方向の距離を計算する関数

    :param d: 星までの距離
    :param theta_unit: 視線方向の角度の単位（degree, arcmin, arcsec）
    :param input_distance_unit: 入力距離の単位（'meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc'）
    :param output_distance_unit: 出力距離の単位（'meter', 'cm', 'km', 'au', 'ly', 'pc', 'kpc'）
    :return: 視線垂直方向の距離（指定された単位）
    """
    # 入力距離をメートルに変換
    d_meters = convert_distance(d, input_distance_unit, 'meter')

    # 角度をラジアンに変換
    theta_rad = ANGLE_UNITS_TO_RADIANS[theta_unit]

    # 視線垂直方向の距離をメートルで計算
    d_perp_meters = 2 * d_meters * math.tan(theta_rad / 2)

    # 結果を指定された出力単位に変換して返す
    d_perp_converted = convert_distance(d_perp_meters, 'meter', output_distance_unit)
    
    # 計算結果を出力
    print(f"1 {theta_unit} = {d_perp_converted:.6e} {output_distance_unit} (at a distance of {d} {input_distance_unit})")
    
    return d_perp_converted

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up