はじめに
前回の記事
では、猿に適当にルービックキュープを解いてもらいました。本記事では、適当に回して完成状態の1手前の状態にして、そこから1手で確実に解くことができる賢い猿にルービックキューブを解いてもらいます。人間だとこの解き方は自然にできて、適当に回して完成状態の1手前の状態にできれば、最後の1手は誰もが容易に解くことができるでしょう。
では、最後の1手を知る賢い猿に2×2×2のルービックキューブを解いてもらいましょう。
実装
本記事は、
を参考に作成されている。この記事を[1]とする。一部コードも引用しているため、引用箇所を方法の項で明記する。
Google Colabで作成した本記事のコードは、こちらにあります。
各種インポート
import random
import numpy as np
import matplotlib.pyplot as plt
実行時の各種バージョン
| Name | Version |
|---|---|
| numpy | 1.21.6 |
| matplotlib | 3.2.2 |
方法
ルービックキューブの状態を表すクラスを用意する。[1]の記事から、 apply_moveまでのcp, coの操作箇所を引用している。状態の説明は[1]の記事を参照されたい。
基本的に【無限の猿定理】ルービックキューブを猿に解かせてみた(Part1: 普通の猿)の記事に書いてある部分の説明を割愛する。
-
is_reach_solved: 完成状態の1手前の状態を判定するメソッドである。完成状態の1手前の状態は9種類ある。
class State:
"""
ルービックキューブの状態を表すクラス
"""
def __init__(self, cp, co):
self.cp = cp
self.co = co
def apply_move(self, move):
"""
操作を適用し、新しい状態を返す
"""
new_cp = [self.cp[p] for p in move.cp]
new_co = [(self.co[p] + move.co[i]) % 3 for i, p in enumerate(move.cp)]
return State(new_cp, new_co)
def apply_scramble(self, moves, moves_num):
"""
適当に崩した状態を返す
moves: 9種類の1手操作
moves_num: 適当に回す回数
"""
faces = sorted(list(moves.keys()))
list_noF = [3, 4, 5, 6, 7, 8]
list_noL = [6, 7, 8, 0, 1, 2]
list_noU = [0, 1, 2, 3, 4, 5]
choice_list = [list_noF, list_noL, list_noU]
choice_next = random.randrange(3)
for _ in range(moves_num):
rand = random.choice(choice_list[choice_next])
move_state = moves[faces[rand]]
self = self.apply_move(move_state)
choice_next = rand // 3
return State(self.cp, self.co)
def is_solved(self):
"""
完成状態か判定
"""
return (self.co == [0, 0, 0, 0, 0, 0, 0, 0] and self.cp == [0, 1, 2, 3, 4, 5, 6, 7])
def is_reach_solved(self, moves):
"""
残り1手で完成状態になるか判定
moves: 9種類の1手操作
"""
faces = list(moves.keys())
for face_name in faces:
move = moves[face_name]
if (self.co == move.co and self.cp == move.cp):
return True
return False
完成状態の1手前の状態まで適当に回して解く
完成状態の1手前まで揃えたら、そこから1手で揃えることができると仮定して書いたコードである。適当に崩した初手の状態が完成状態である場合も考慮している。
# 9種類の1手操作を全部定義する
moves = {
'U': State([3, 0, 1, 2, 4, 5, 6, 7],
[0, 0, 0, 0, 0, 0, 0, 0]),
'L': State([4, 1, 2, 0, 7, 5, 6, 3],
[2, 0, 0, 1, 1, 0, 0, 2]),
'F': State([0, 1, 3, 7, 4, 5, 2, 6],
[0, 0, 1, 2, 0, 0, 2, 1]
)}
faces = list(moves.keys())
for face_name in faces:
moves[face_name + '2'] = moves[face_name].apply_move(moves[face_name])
moves[face_name + '\''] = moves[face_name].apply_move(moves[face_name]).apply_move(moves[face_name])
# 完成状態を用意
solved_state = State(
[0, 1, 2, 3, 4, 5, 6, 7],
[0, 0, 0, 0, 0, 0, 0, 0]
)
# 完成状態から100回適当に回して崩す
scrambled_state = solved_state.apply_scramble(moves=moves, moves_num=100)
# 同じ面を続けて回さないようにするためのリスト
faces = sorted(list(moves.keys()))
list_noF = [3, 4, 5, 6, 7, 8]
list_noL = [6, 7, 8, 0, 1, 2]
list_noU = [0, 1, 2, 3, 4, 5]
choice_list = [list_noF, list_noL, list_noU]
if scrambled_state.is_solved():
# 初手で完成状態か判定
print(f'It was solved in 0 moves.')
else:
choice_next = random.randrange(3)
for num_move in range(100000000):
if scrambled_state.is_reach_solved(moves):
print(f'It was solved in {num_move + 1} moves.')
break
rand = random.choice(choice_list[choice_next])
move_state = moves[faces[rand]]
scrambled_state = scrambled_state.apply_move(move_state)
choice_next = rand // 3
else:
print(f'It could not be solved in {num_move + 1} moves.')
It was solved in 719531 moves.
1万個の異なるルービックキューブを同様にして解くコード
完成状態の1手前の状態まで適当に回して解くの項のコードを1万回試行する。つまり、1万個の異なるルービックキューブを解く。事前に1万回試行した結果は、nums_reach_solve_move.npyより、ダウンロードできる。以降、こちらのファイルを使用する。
import random
import numpy as np
def main():
# 9種類の1手操作を全部定義する
moves = {
'U': State([3, 0, 1, 2, 4, 5, 6, 7],
[0, 0, 0, 0, 0, 0, 0, 0]),
'L': State([4, 1, 2, 0, 7, 5, 6, 3],
[2, 0, 0, 1, 1, 0, 0, 2]),
'F': State([0, 1, 3, 7, 4, 5, 2, 6],
[0, 0, 1, 2, 0, 0, 2, 1]
)}
faces = list(moves.keys())
for face_name in faces:
moves[face_name + '2'] = moves[face_name].apply_move(moves[face_name])
moves[face_name + '\''] = moves[face_name].apply_move(moves[face_name]).apply_move(moves[face_name])
random.seed(2022) # 再現性のため乱数の種を指定
# 完成状態を用意
solved_state = State(
[0, 1, 2, 3, 4, 5, 6, 7],
[0, 0, 0, 0, 0, 0, 0, 0]
)
trials = 10000 # 試行回数
nums_solve_move= np.zeros(trials) # 保存先の配列
# 同じ面を連続で回さないようにするためのリスト
faces = sorted(list(moves.keys()))
list_noF = [3, 4, 5, 6, 7, 8]
list_noL = [6, 7, 8, 0, 1, 2]
list_noU = [0, 1, 2, 3, 4, 5]
choice_list = [list_noF, list_noL, list_noU]
for trial in range(trials):
print(f'[trial num {trial}]')
# 完成状態から100回適当に回して崩す
scrambled_state = solved_state.apply_scramble(moves=moves, moves_num=100)
if scrambled_state.is_solved():
# 初手で完成状態か判定
print(f'It was solved in 0 moves.')
else:
choice_next = random.randrange(3)
for num_move in range(100000000):
if scrambled_state.is_reach_solved(moves):
print(f'It was solved in {num_move + 1} moves.')
nums_solve_move[trial] = num_move + 1
break
rand = random.choice(choice_list[choice_next])
move_state = moves[faces[rand]]
scrambled_state = scrambled_state.apply_move(move_state)
choice_next = rand // 3
else:
print(f'It could not be solved in {num_move + 1} moves.')
nums_solve_move[trial] = np.nan
np.save('nums_reach_solve_move.npy', nums_solve_move)
class State:
"""
ルービックキューブの状態を表すクラス
"""
def __init__(self, cp, co):
self.cp = cp
self.co = co
def apply_move(self, move):
"""
操作を適用し、新しい状態を返す
"""
new_cp = [self.cp[p] for p in move.cp]
new_co = [(self.co[p] + move.co[i]) % 3 for i, p in enumerate(move.cp)]
return State(new_cp, new_co)
def apply_scramble(self, moves, moves_num):
"""
適当に崩した状態を返す
moves: 9種類の1手操作
moves_num: 適当に回す回数
"""
faces = sorted(list(moves.keys()))
list_noF = [3, 4, 5, 6, 7, 8]
list_noL = [6, 7, 8, 0, 1, 2]
list_noU = [0, 1, 2, 3, 4, 5]
choice_list = [list_noF, list_noL, list_noU]
choice_next = random.randrange(3)
for _ in range(moves_num):
rand = random.choice(choice_list[choice_next])
move_state = moves[faces[rand]]
self = self.apply_move(move_state)
choice_next = rand // 3
return State(self.cp, self.co)
def is_solved(self):
"""
完成状態か判定
"""
return (self.co == [0, 0, 0, 0, 0, 0, 0, 0] and self.cp == [0, 1, 2, 3, 4, 5, 6, 7])
def is_reach_solved(self, moves):
"""
残り1手で完成状態になるか判定
moves: 9種類の1手操作
"""
faces = list(moves.keys())
for face_name in faces:
move = moves[face_name]
if (self.co == move.co and self.cp == move.cp):
return True
return False
if __name__ == '__main__':
main()
結果
事前に1万回試行した結果は、nums_reach_solve_move.npyより、ダウンロードできる。
nums_reach_solve_move = np.load('nums_reach_solve_move.npy')
# 統計情報
print('試行回数:', len(nums_reach_solve_move))
print('平均値:', round(np.mean(nums_reach_solve_move)))
print('中央値:', int(np.median(nums_reach_solve_move)))
print('不偏標準偏差:', round(np.std(nums_reach_solve_move,ddof=1)))
print('最小値:', int(np.min(nums_reach_solve_move)))
print('最大値:', int(np.max(nums_reach_solve_move)))
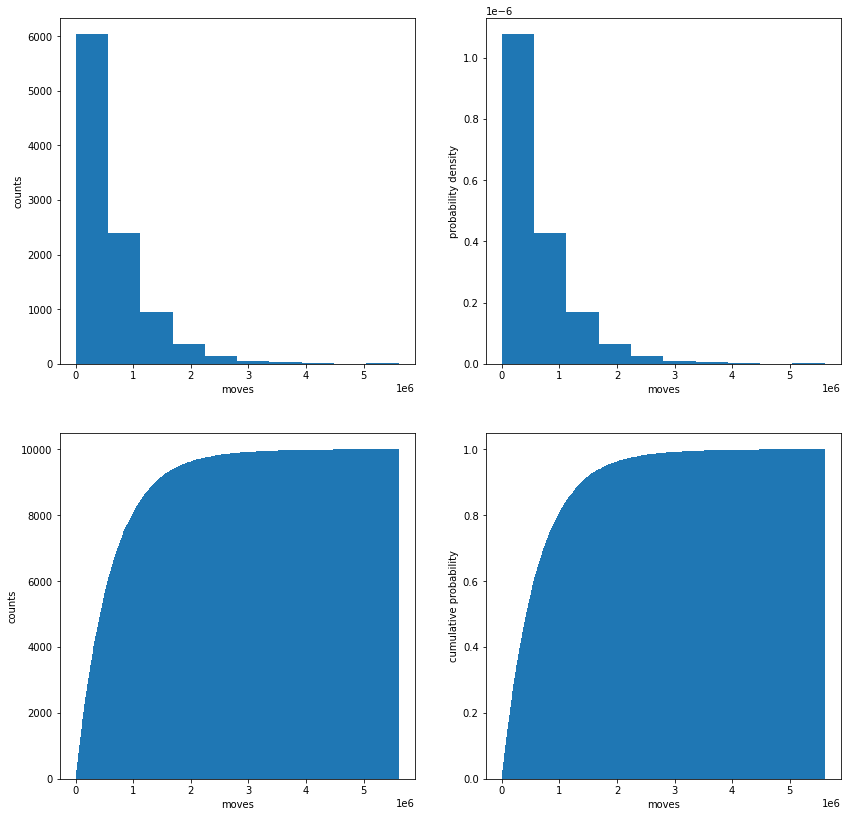
# ヒストグラムに表示
fig, axs = plt.subplots(2, 2, figsize=(14, 14))
axs[0, 0].hist(nums_reach_solve_move)
axs[0, 0].set_xlabel('moves')
axs[0, 0].set_ylabel('counts')
axs[0, 1].hist(nums_reach_solve_move, density=True)
axs[0, 1].set_xlabel('moves')
axs[0, 1].set_ylabel('probability density')
axs[1, 0].hist(nums_reach_solve_move, bins=1000, cumulative=True)
axs[1, 0].set_xlabel('moves')
axs[1, 0].set_ylabel('counts')
axs[1, 1].hist(nums_reach_solve_move, bins=1000, density=True, cumulative=True)
axs[1, 1].set_xlabel('moves')
axs[1, 1].set_ylabel('cumulative probability')
plt.show()
出力結果
試行回数: 10000
平均値: 606413
中央値: 423307
不偏標準偏差: 605717
最小値: 24
最大値: 5605335
平均が約60万回となりました。
ちなみに、60万回で解けた場合、どれくらい時間がかかるでしょうか。1秒に1回回す賢い猿に1日1時間ルービックキューブで遊ばせた場合、
\frac{600000\ 回}{3600\ 回/日} = 167\ 日
となる。約6ヶ月で解けてしまうので、適当に回して解く普通の猿は同様のペースで約3年かけて解くので、6倍も早く解くことができる賢い猿はさすがですね。
考察
結果のヒストグラムの分布は数学的に何に従うのでしょうか。ここで、ルービックキューブの取り得る組み合わせは、wikipediaによると、以下の通りである。
コーナーキューブの取り得る位置の順列が8!通り、コーナーキューブが独立に取り得る向きは37通り、空間に対するキューブの向きは24通りある。
よって考えられる組み合わせは:
{\frac {8!\times 3^{7}}{24}}=7!\times 3^{6}=3674160
(wikipedia ポケットキュープより引用)
前回の記事より、ルービックキューブを適当に解いた分布は1/3674160の確率分布であった。単純に考えると、1手前までの状態が9個あり、完成状態の1個で合わせて10個の状態があるので、10/3674160の確率分布となると考えがちですがそれでは問題である。任意の10個の状態に揃うまでの分布は、10/3674160の確率分布であると予想できるが、今回の場合は完成状態と1手前の状態は密接に関係しているので非常に偏った状態を選ぶことになり、10/3674160の確率分布には従わない。
今回の場合は、完成状態から逆算すると想像しやすくなる。まず、完成状態だけの分布を考えた場合は、1/3674160の確率分布である。そして、1手前から完成状態になる確率は1/6(同じ面を連続で回さないので、各面×角度2×3=6通り)なので、完成状態の1手前から完成状態を確実に解く場合は、6/3674160の確率分布に従うと考えられる。
当たる確率が6/3674160のくじ引きの当たるまでの分布
当たる確率$p$が$p=6/3674160$のくじ引きを引いたくじを元に戻すとき当たるまでに引く回数$moves$は、$moves$回外れを引いて$moves$回目で当たりを引くので、
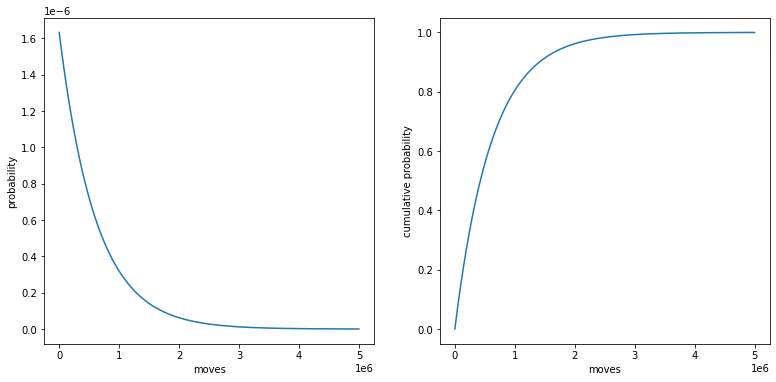
P(moves)=p(1-p)^{moves}
となる。この式をグラフで表す。
moves = 5000000
p = 6 / 3674160
probability = [p*(1-p)**move for move in range(moves)]
cumsum_probability = np.cumsum(probability)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13, 6))
# 確率分布を表示
ax1.plot(np.arange(moves)[::100], probability[::100])
ax1.set_xlabel('moves')
ax1.set_ylabel('probability')
# 累積確率分布を表示
ax2.plot(np.arange(moves)[::100], cumsum_probability[::100])
ax2.set_xlabel('moves')
ax2.set_ylabel('cumulative probability')
plt.show()
*[::100]としている理由は、プロット点が多すぎるとグラフに表示するまでの時間がかるためである。500万点も表示する必要もないので、100点置きに5万点プロットしている。
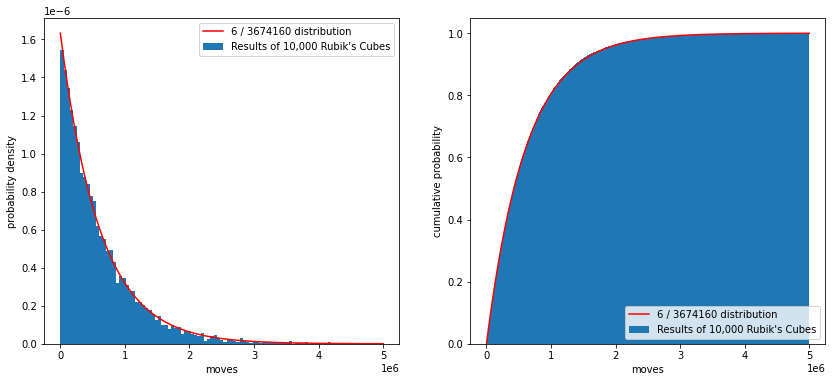
6 / 3674160で当たりが出るくじの確率分布と結果を重ねて表示
当たる確率が6/3674160のくじ引きの当たるまでの分布と結果を重ねて表示する。
事前に1万回試行した結果は、nums_reach_solve_move.npyより、ダウンロードできる。
moves = 5000000
nums_reach_solve_move = np.load('nums_reach_solve_move.npy')
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# 確率分布を表示
ax1.hist(nums_reach_solve_move, bins=np.linspace(0, moves, 100), density=True,
label="Results of 10,000 Rubik's Cubes")
ax1.plot(np.arange(moves)[::100], probability[::100], color='red', label='6 / 3674160 distribution')
ax1.set_xlabel('moves')
ax1.set_ylabel('probability density')
ax1.legend()
# 累積確率分布を表示
ax2.hist(nums_reach_solve_move, bins=np.linspace(0, moves, 1000), density=True, cumulative=True,
label="Results of 10,000 Rubik's Cubes")
ax2.plot(np.arange(moves)[::100], cumsum_probability[::100], color='red', label='6 / 3674160 distribution')
ax2.set_xlabel('moves')
ax2.set_ylabel('cumulative probability')
ax2.legend()
plt.show()
確かに見た目が一致していることがわかる。
おまけ(3×3×3のルービックキューブを1手前の状態まで適当に回した回数の分布の予想)
3×3×3のルービックキューブの取り得る組み合わせは、wikipediaによると、以下の通りである。
ルービックキューブをいったん分解して組み立てなおしたときに考えられる色の配置の総数を求めると、まずコーナーキューブの位置が$8!$通り、向きが$38$通り、エッジキューブの位置が$12!$通り、向きが$2^{12}$通り、これらを全てかけあわせて$(8!×38)×(12!×2^{12})$通りとなる。しかし、実際には完全に揃った状態のキューブに回転操作を施すだけではこれだけの組み合わせは実現できない。
- コーナーキューブとエッジキューブの順列の偶奇は一致する
- 全てのエッジキューブの位置が揃っている場合、向きが異なっているエッジキューブの個数は偶数個である
- 全てのコーナーキューブの位置が揃っている場合、時計回りに向きがずれているコーナーキューブの個数と反時計回りに向きがずれているコーナーキューブの個数は3を法として合同である
以上の3つの条件から、完全に揃った状態のキューブに回転操作を施してできる組み合わせの総数は前述の値を$(2×2×3)$で割ったものとなる。逆に、上記の3つの条件を満たしていれば6面がそろった初期状態に戻すことができる。すなわち、このパズルで考えられる配置は
\frac{(8!×38)×(12!×212)}{2×2×3}=4325京2003兆2744億8985万6000通り
である。
(wikipedia ルービックキューブより引用)
考察の項から、3×3×3のルービックキューブを1手前の状態まで適当に回して解くまでに回した回数の分布は、15/43252003274489856000の確率分布であると考えられる。(完成状態の1手前から完成状態になる確率は、同じ面を連続で回さないので、各面×角度5×3=15通りより、1/15である。)
もし、4325京回/15で解けるとして、世界人口80億人全ての人に3×3×3のルービックキューブを与え、1秒に1回1日8時間適当に回してもらった場合は、
\frac{4325 \times 10^{16}\ 回\ / \ 15}{28800\ 回/日 \times 80\times 10^8\ 人 } \sim 13000 \ 日/人 \sim 36\ 年/人
となる。つまり、36年に誰か1人は適当に回して3×3×3のルービックキューブを解くことができる。適当に解いた場合の15倍も効率的に解くことができました。
まとめ
以上より、2×2×2のルービックキューブを完成状態の1手前まで適当に回して解いた回数は、適当に解く場合の6倍効率的に解くことでき、「当たりが6本ある3674160(2×2×2のルービックキューブの組み合わせの総数)本のくじ引きで当たりが出るまで引いた回数は?ただし、引いたくじは元に戻す。」という問題設定と同値であると考えられる。
この考え方に基づいて、3×3×3のルービックキューブでは約4325京通りの組み合わせがあり完成状態の1手前まで適当に回して解いた場合、適当に解く場合の15倍効率的に解くことでき、世界人口80億人全ての人に3×3×3のルービックキューブを与え、1秒に1回1日8時間適当に回してもらった場合は約36年かかることになる。
このように、1手前の状態を覚えているだけで相当早く揃えることができ、ルービックキューブにおいても知識があることは重要なのである。
関連記事
参考資料