カウント画像のランダムサンプリングによる超解像度化の実装方法

はじめに

カウント画像は、天文学や光学顕微鏡の画像など、様々な分野で幅広く使用されています。カウント画像の空間スケールを詳しく知るために、画像の実ピクセル以下の空間情報が必要となる場面があります。その一つの手段として超解像があり、古典的な手法であるニアレストネイバー法やバイリニア補間から、最新の機械学習手法まで、さまざまな手法が研究されています。

本記事では、その中でカウント画像の超解像化に広く使われる、非常にオーソドックスなランダム化に基づいた手法について実装方法等を紹介します。

ランダム化による高解像度化

ランダム化による超解像化は以下のようなイメージで実装されます。

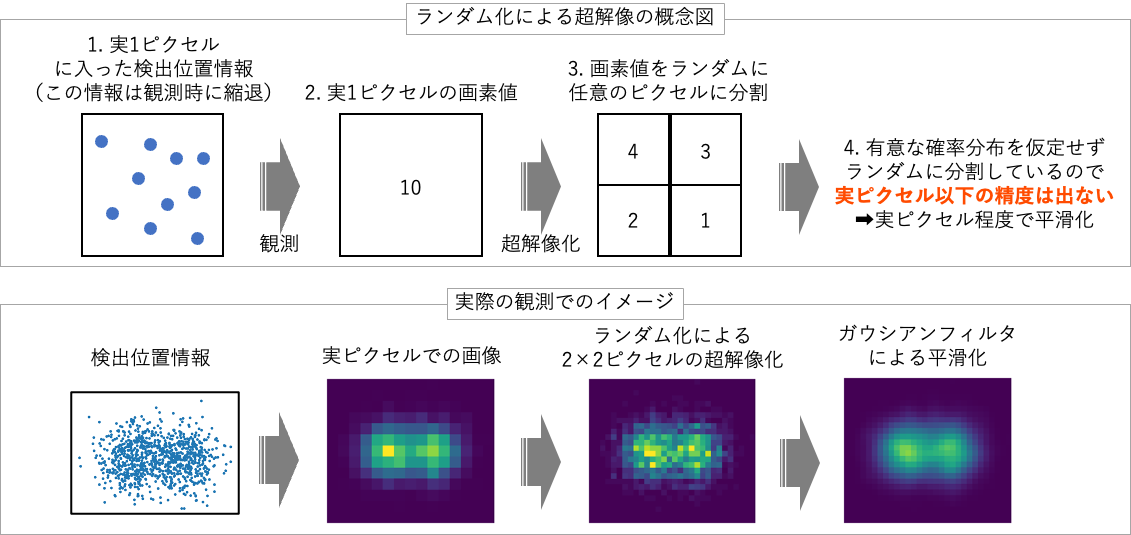
1. 観測されたイベントの空間情報が与えられます。
2. 本来は、手順1のように無限に細かい情報がありますが、観測時に実ピクセル単位でサンプリングされます。
3. ランダム化による超解像化では、ピクセル毎に任意の画素に分割し、ランダムにカウント値を振り分けます。（カウント値のため、振り分けは整数単位になります。）
4. ランダム化による補完は意味のある確率分布を仮定していないため、実ピクセル程度のガウシアンフィルタで平滑化します。

方法

ここでは、2つのガウス分布で得られる簡単なシミュレーション散布図を用いて、実装について紹介します。

本記事で使用したコードはこちらにあります。

0. 各種インポート

import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import gaussian_filter

1. 観測用の散布図の用意

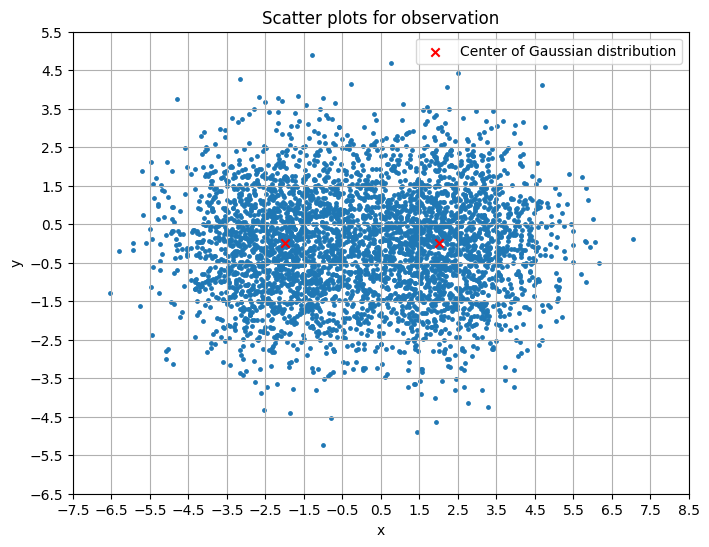
観測用の散布図を用意します。この散布図の各プロットを検出する際にグリッド毎に集計されて観測画像として得られます。

散布図を生成するためのコード

散布図を生成するためのコード

# 2次元ガウシアン分布から乱数の散布図
np.random.seed(2023)
mean_1 = [-2, 0]
mean_2 = [2, 0]
cov = [[2, 0], [0, 2]]
evt_x, evt_y = np.hstack([np.random.multivariate_normal(mean_1, cov, 2000).T, np.random.multivariate_normal(mean_2, cov, 2000).T])

# 単位目盛りあたりのグリッドを作成
x_grid = np.arange(np.floor(evt_x.min())-0.5, np.ceil(evt_x.max())+0.5001, 1)
y_grid = np.arange(np.floor(evt_y.min())-0.5, np.ceil(evt_y.max())+0.5001, 1)

fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(evt_x, evt_y, s=6)
ax.scatter(*mean_1, marker='x', c='red', label='Center of Gaussian distribution')
ax.scatter(*mean_2, marker='x', c='red')
ax.set_title('Scatter plots for observation')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_aspect('equal')
ax.set_xticks(x_grid)
ax.set_yticks(y_grid)
ax.grid(True)
ax.legend()
plt.show()

コードの説明

1. np.random.seed(2023)で再現性のため乱数の種を指定します。
2. x_grid, y_gridの箇所の0.5001は、浮動小数点の影響でnp.arange()の配列の選び方が変わってしまうことを避けるために、0.0001という小さな値を加えています。
3. mean_1, mean_2, covで、(-2,0)と(2,0)を中心とする分散2の2次元ガウス分布に従う乱数を生成します。
4. この後、ヒートマップを作るにあたり見やすくするためにx_grid, y_gridで1目盛りずつグリッドを引きます。このグリッドとピクセルが対応します。

※ガウス分布を見やすくするために、各分布の中心にx印をつけていますが、シミュレーション上で特に意味はないです。

2. 観測画像化

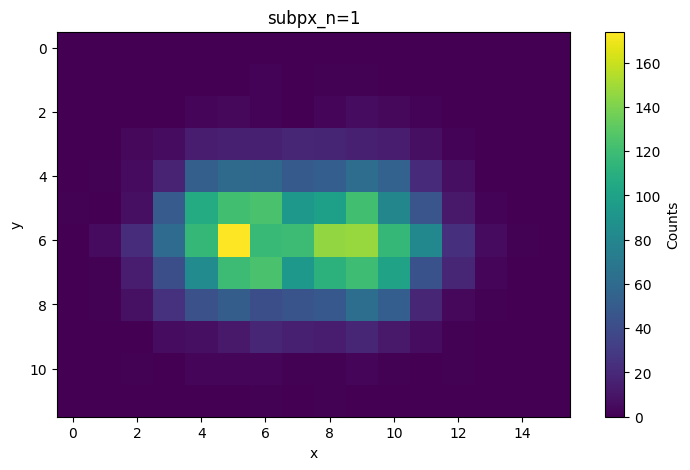
散布図からグリッド毎に集計して観測画像を作ります。

観測画像の作成コード

観測画像の作成コード

# グリッド上のデータ点のカウントを計算
hist, *_ = np.histogram2d(evt_x, evt_y, bins=(x_grid, y_grid))
image = hist.T
fig, ax = plt.subplots(figsize=(9, 5))
cbar = ax.imshow(image, vmin=0, vmax=image.max())
fig.colorbar(cbar, label='Counts')
ax.set_title('subpx_n=1')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_aspect('equal')
plt.show()

コードの説明

1. np.histogram2d(evt_x, evt_y, bins=(x_grid, y_grid))で、グリッド毎の2次元ヒストグラムを得ます。
2. image = hist.Tは、histに配列が(x,y)の順で入っているので、ax.imshow()で読み込めるように(y,x)に変換します。

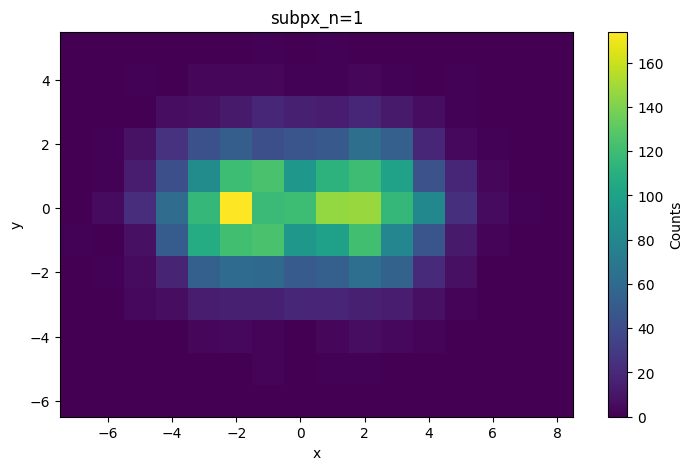
※もちろん、numpyではなくmaptplotlibのモジュールで2次元ヒストグラムを表示することもできます。本記事では、この先の超解像化で画像として扱うためnumpyで計算しますが、下記に散布図の座標を保持したヒストグラムの参考コードを載せておきます。

matplotlibのhist2dによる散布図の座標系を保持した表示コード

matplotlibのhist2dでの表示コード

fig, ax = plt.subplots(figsize=(9, 5))
*_, cbar = ax.hist2d(evt_x, evt_y, bins=(x_grid, y_grid), vmin=0, vmax=image.max())
fig.colorbar(cbar, label='Counts')
ax.set_title('subpx_n=1')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_aspect('equal')
plt.show()

(x,y)が散布図の座標とリンクしているのがわかります。このコードは、ただ散布図をヒストグラム化しただけですが、超解像化した場合の座標の保持を行う場合は結構な工夫が必要となります。

3. ランダム化による超解像化

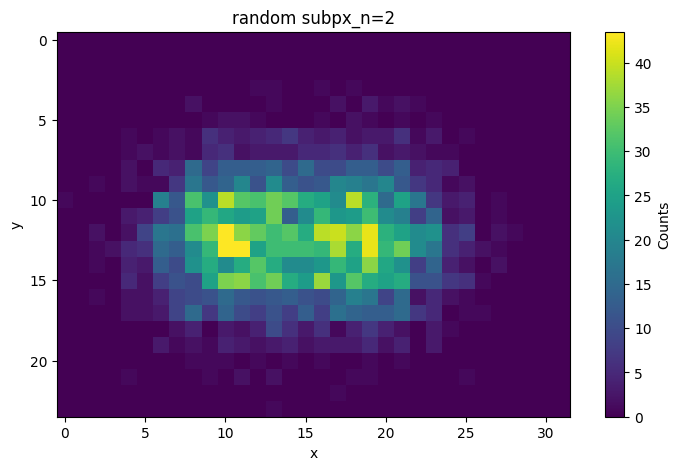
観測画像をピクセル毎にピクセル値に従い1カウントずつランダムに4つの領域に振り分けて超解像化します。
得られた画像のサイズが2×2倍増えていることが確認できます。

ランダム化による超解像化コード

ランダム化による超解像化コード

def random_subpx(image, subpx_n):
    """ランダム化による超解像化
    Args:
        image (ndarray): 超解像度化を行う入力画像。整数値のNumPy配列を想定
        subpx_n (int): 各ピクセルをsubpx_n×subpx_n個のサブピクセルに分割するかを指定する整数

    Returns:
        ndarray: 入力画像を超解像画像。
    """
    np.random.seed(2023)
    image = image.astype(np.int64)
    subpx_image = np.zeros((image.shape[0] * subpx_n, image.shape[1] * subpx_n), dtype=np.int64)
    for y in range(image.shape[0]):
        for x in range(image.shape[1]):
            px_val = image[y, x]
            rand_ys = np.random.randint(0, subpx_n, size=px_val)
            rand_xs = np.random.randint(0, subpx_n, size=px_val)
            for (rand_y, rand_x) in zip(rand_ys, rand_xs):
                subpx_image[y*subpx_n+rand_y, x*subpx_n+rand_x] += 1
    return subpx_image

# ランダム化によるサブピクセル化した画像を作成（ピクセル毎にsubpx_n×subpx_nに分割）
subpx_n = 2
subpx_image = random_subpx(image, subpx_n)

fig, ax = plt.subplots(figsize=(9, 5))
cbar = ax.imshow(subpx_image, vmin=0, vmax=image.max()/(subpx_n**2))
fig.colorbar(cbar, label='Counts')
ax.set_title(f'random {subpx_n=}')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_aspect('equal')
plt.show()

コードの説明

1. random_sbpx(image, subpx_n)で、各ピクセルを値に基づきsubpx_n×subpx_nにランダムに割り振け超解像化します。
2. ax.imshow()のvmax=image.max()/(subpx_n**2)は、超解像前の解像度におけるカラー範囲に規格化するためにsubpx_n**2で割っています。

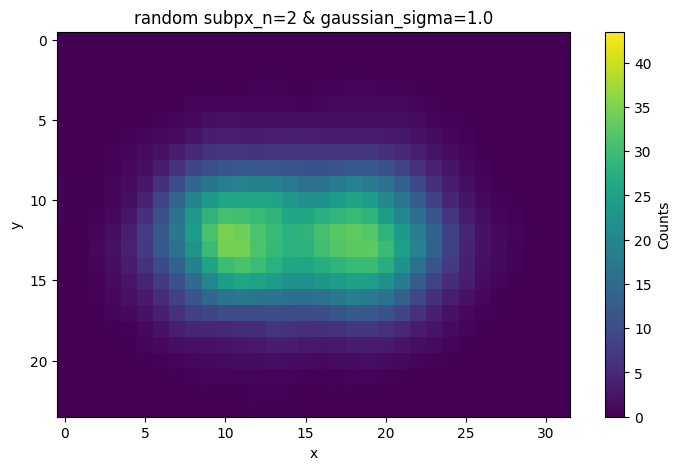
4. ガウシアンフィルタによる平滑化

ランダム化は意味のある確率分布を前提とした処理ではないため、超解像化された画像自体は誤差の影響を受けやすく、したがって、元の観測画像のスケールに近い平滑化を行う必要があります。

ここでは、元の観測画像のスケール程度としてガウシアンσをσ=0.5としています。このσのパラメータ値は元の観測画像の1ピクセルに1σの情報が含まれることを示しています。

ガウシアン平滑化のコード

ガウシアン平滑化のコード

# ガウシアン平滑化
gaussian_sigma = subpx_n / 2
subpx_gaussian_image = gaussian_filter(subpx_image, sigma=gaussian_sigma, output=np.float64)

fig, ax = plt.subplots(figsize=(9, 5))
cbar = ax.imshow(subpx_gaussian_image, vmin=0, vmax=image.max()/(subpx_n**2))
fig.colorbar(cbar, label='Counts')
ax.set_title(f'random {subpx_n=} & {gaussian_sigma=}')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_aspect('equal')
plt.show()

コードの説明

1. gaussian_sigma = subpx_n / 2は、グリッドが1×1のときの観測画像と同程度の空間スケールにするための平滑化のため使っています。このパラメータにより、1×1のピクセルサイズに1σ入る計算となります。
2. SciPyのgaussian_filter()関数内でのoutput=np.float64は結構重要な部分です。 subpx_imageは整数型のデータのため、outputパラメータを指定しないと、出力も整数型になり、統計的な情報が少ない画像に対しては丸め込まれてしまい平滑化が正しく行えないためです。

精度の検証

ここでは、超解像画像の精度検証のため、散布図からグリッドサイズを調整して直接作成した本物の観測画像と比較します。

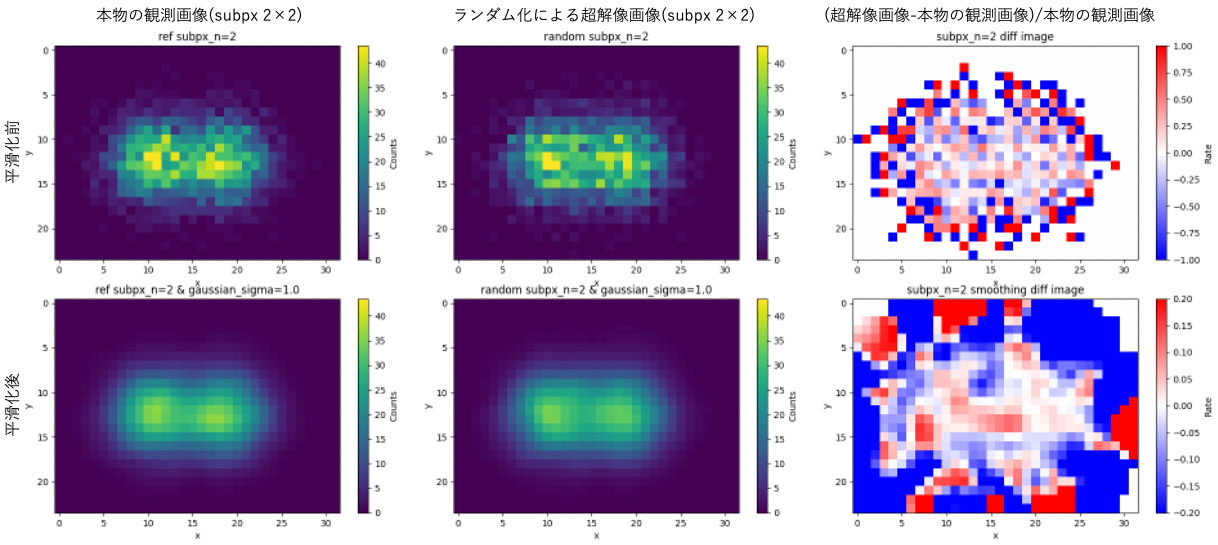
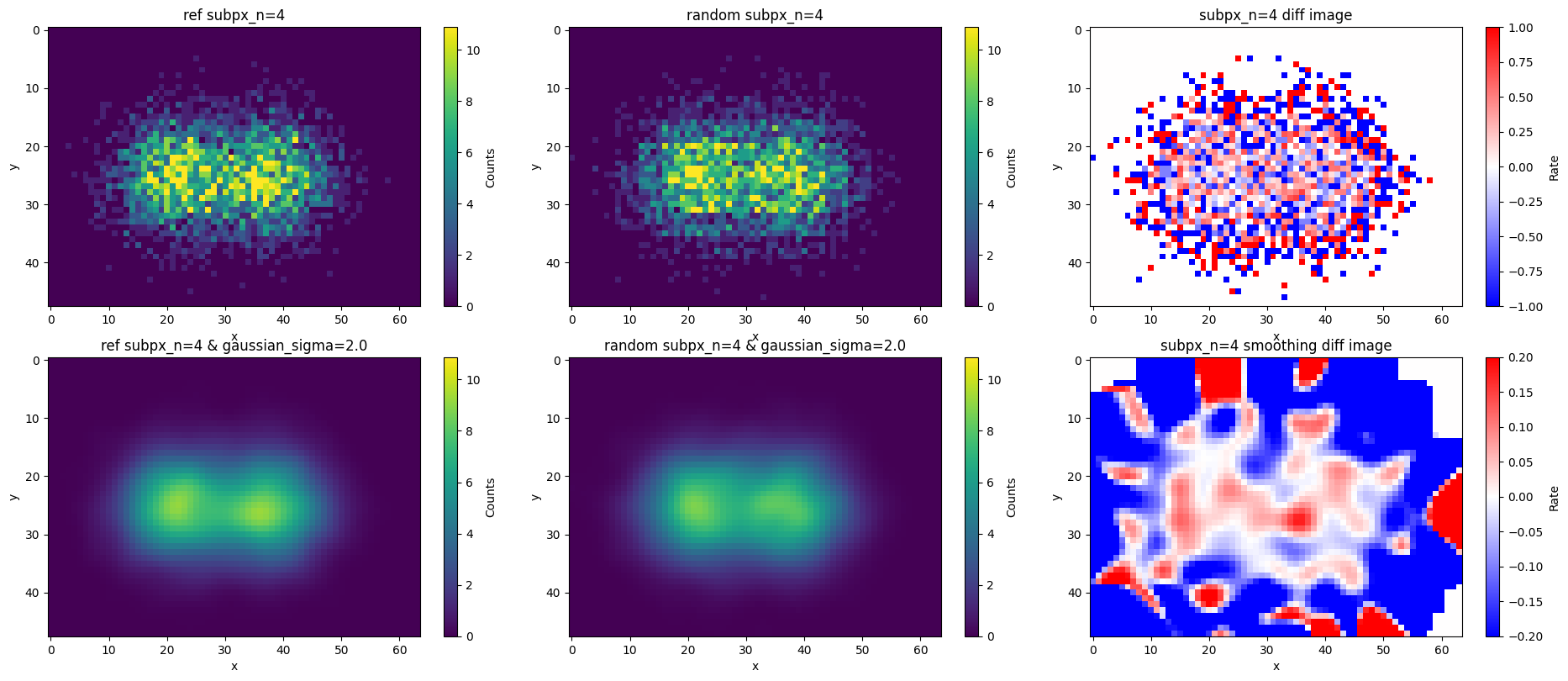
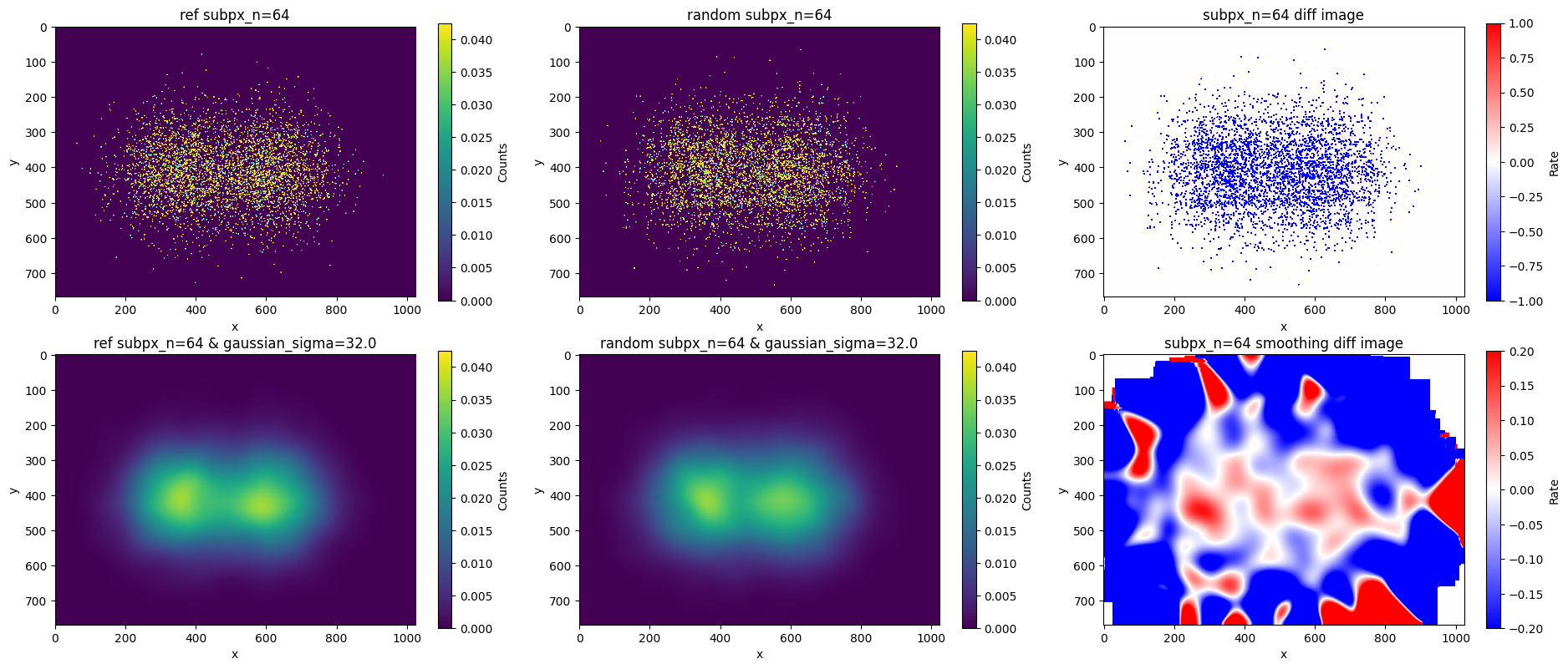
下図の説明です。

• 左図：散布図のグリッドの座標を0.5×0.5でサンプリングした本物の観測画像。
• 中央図：散布図を1×1のグリッドでサンプリングした画像をランダム化によって超解像化した画像。
• 右図：（左の画像-中央の画像）/ 左の画像を取ることで、左図を基準としたときの変動率を表したもの。
• 上段：平滑化する前の画像。
• 下段：観測画像の1×1のスケール（σ=0.5）でガウシアン平滑化後の画像。

上図上段より、平滑化前ではカウントが30付近の明るい領域で、±20%程度の変動率が見られ統計誤差の範囲内($30/\sqrt 30 \sim 0.18 = 18\%$)で、ある程度説明できることがわかります。
また、下段の1×1のグリッドのスケールに平滑化後の結果では、1×1におけるカウントレートが100であることから、統計誤差（$100/\sqrt 100 \sim 0.1 = 10\%$）は10%程度であり、その範囲内で一致していることがわかります。

精度検証用のコード

精度検証用のコード

fig, axs = plt.subplots(2, 3, figsize=(19, 8))

# リファレンス画像（散布図からスケールに合わせたグリッドで作成した元画像）
x_grid = np.arange(np.floor(evt_x.min())-0.5, np.ceil(evt_x.max())+0.5001, 1 / subpx_n)
y_grid = np.arange(np.floor(evt_y.min())-0.5, np.ceil(evt_y.max())+0.5001, 1 / subpx_n)
hist, *_ = np.histogram2d(evt_x, evt_y, bins=(x_grid, y_grid))
ref_image = hist.T

cbar = axs[0, 0].imshow(ref_image, vmin=0, vmax=image.max()/(subpx_n**2))
fig.colorbar(cbar, label='Counts')
axs[0, 0].set_title(f'ref {subpx_n=}')
axs[0, 0].set_xlabel('x')
axs[0, 0].set_ylabel('y')
axs[0, 0].set_aspect('equal')

# ランダム化によるサブピクセル化した画像を作成
subpx_n = 2
subpx_image = random_subpx(image, subpx_n)

cbar = axs[0, 1].imshow(subpx_image, vmin=0, vmax=image.max()/(subpx_n**2))
fig.colorbar(cbar, label='Counts')
axs[0, 1].set_title(f'random {subpx_n=}')
axs[0, 1].set_xlabel('x')
axs[0, 1].set_ylabel('y')
axs[0, 1].set_aspect('equal')

# リファレンス画像との差分
diff_image = (ref_image - subpx_image) / (ref_image + 1e-15)
cbar = axs[0, 2].imshow(diff_image, vmin=-1.0, vmax=1.0, cmap='bwr')
fig.colorbar(cbar, label='Rate')
axs[0, 2].set_title(f'{subpx_n=} diff image')
axs[0, 2].set_xlabel('x')
axs[0, 2].set_ylabel('y')
axs[0, 2].set_aspect('equal')

# ガウシアン平滑化パラメータ
gaussian_sigma = subpx_n / 2

# リファレンス画像のガウシアン平滑化
ref_gaussian_image = gaussian_filter(ref_image, sigma=gaussian_sigma, output=np.float64)

cbar = axs[1, 0].imshow(ref_gaussian_image, vmin=0, vmax=image.max()/(subpx_n**2))
fig.colorbar(cbar, label='Counts')
axs[1, 0].set_title(f'ref {subpx_n=} & {gaussian_sigma=}')
axs[1, 0].set_xlabel('x')
axs[1, 0].set_ylabel('y')
axs[1, 0].set_aspect('equal')

# ランダム超解像化した画像のガウシアン平滑化
subpx_gaussian_image = gaussian_filter(subpx_image, sigma=gaussian_sigma, output=np.float64)

cbar = axs[1, 1].imshow(subpx_gaussian_image, vmin=0, vmax=image.max()/(subpx_n**2))
fig.colorbar(cbar, label='Counts')
axs[1, 1].set_title(f'random {subpx_n=} & {gaussian_sigma=}')
axs[1, 1].set_xlabel('x')
axs[1, 1].set_ylabel('y')
axs[1, 1].set_aspect('equal')

# ガウシアン平滑化後のリファレンス画像との差分
diff_smoothig_image = (ref_gaussian_image - subpx_gaussian_image) / (ref_gaussian_image + 1e-15)
cbar = axs[1, 2].imshow(diff_smoothig_image, vmin=-0.2, vmax=0.2, cmap='bwr')
fig.colorbar(cbar, label='Rate')
axs[1, 2].set_title(f'{subpx_n=} smoothing diff image')
axs[1, 2].set_xlabel('x')
axs[1, 2].set_ylabel('y')
axs[1, 2].set_aspect('equal')

fig.tight_layout()
plt.show()

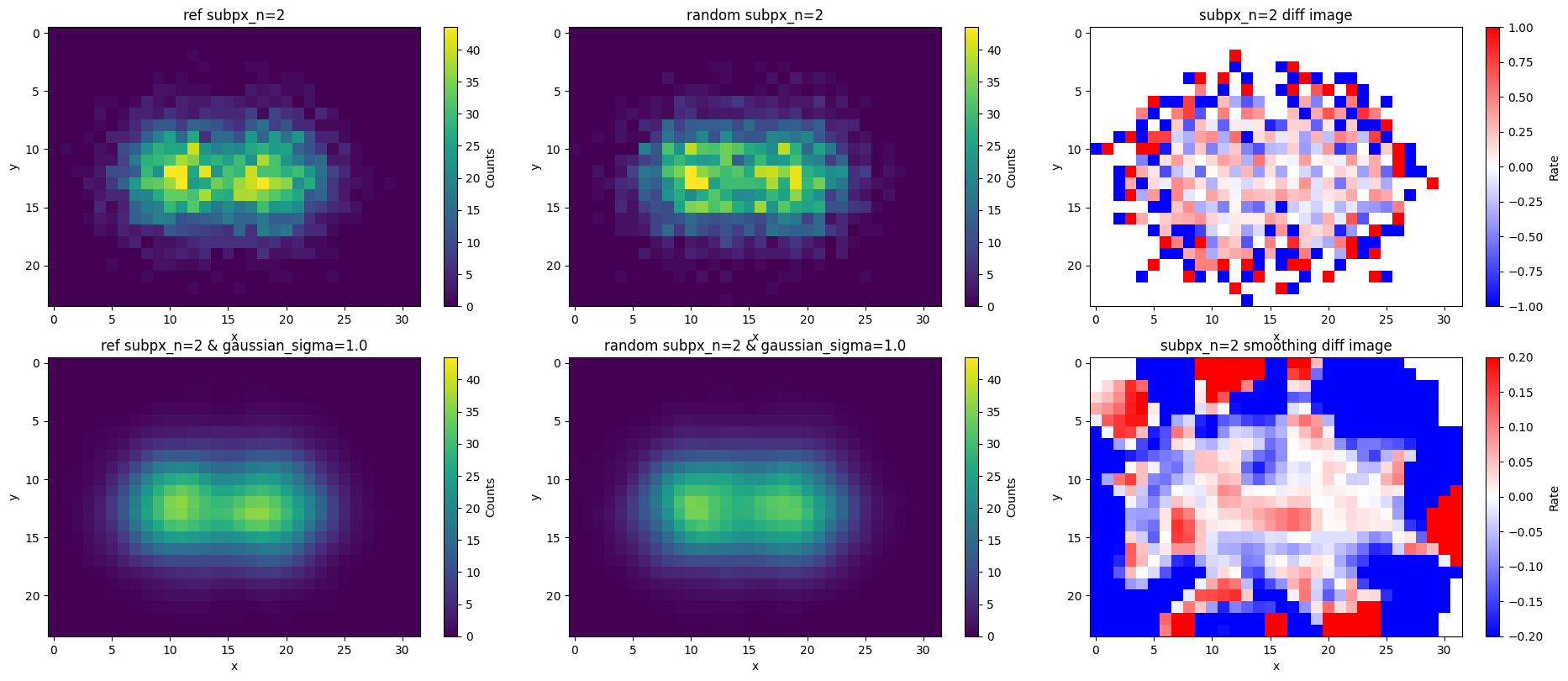
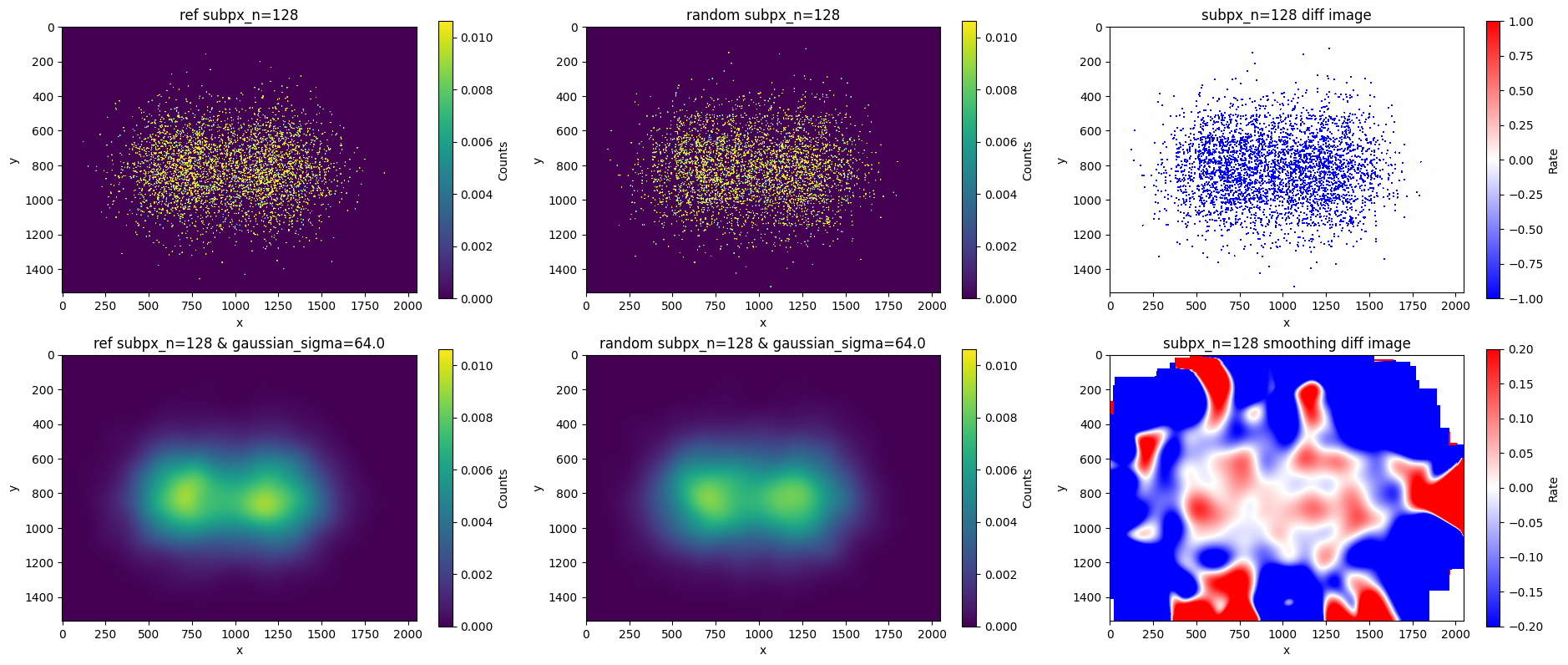
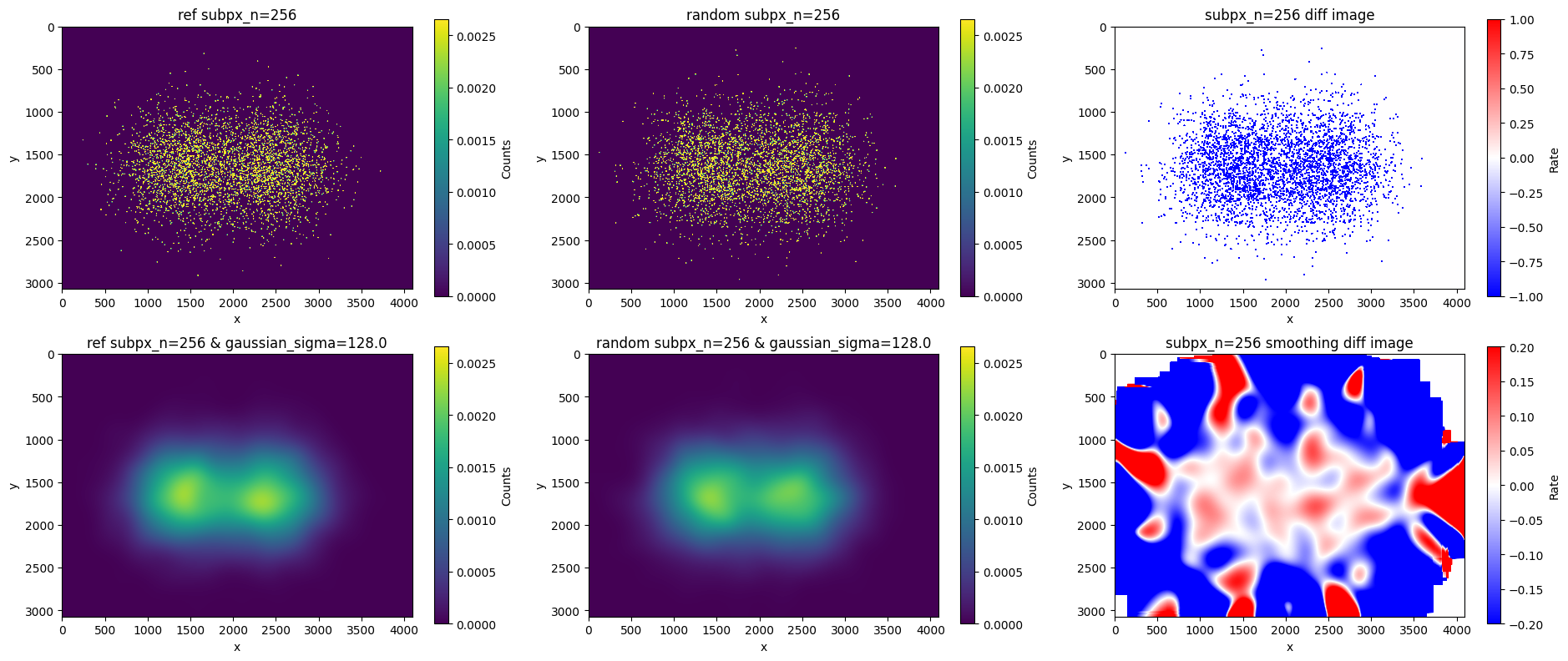
その他の超解像サイズのパラメータによる結果

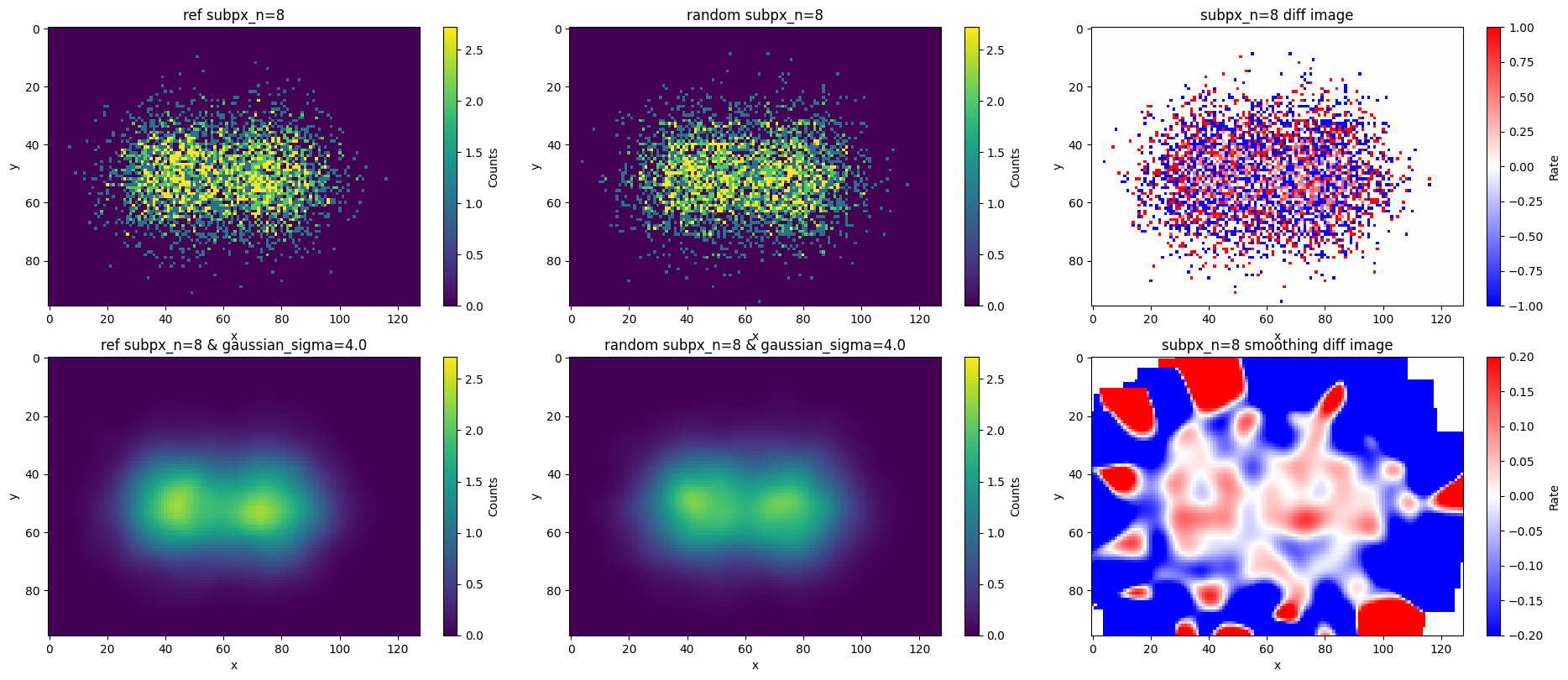
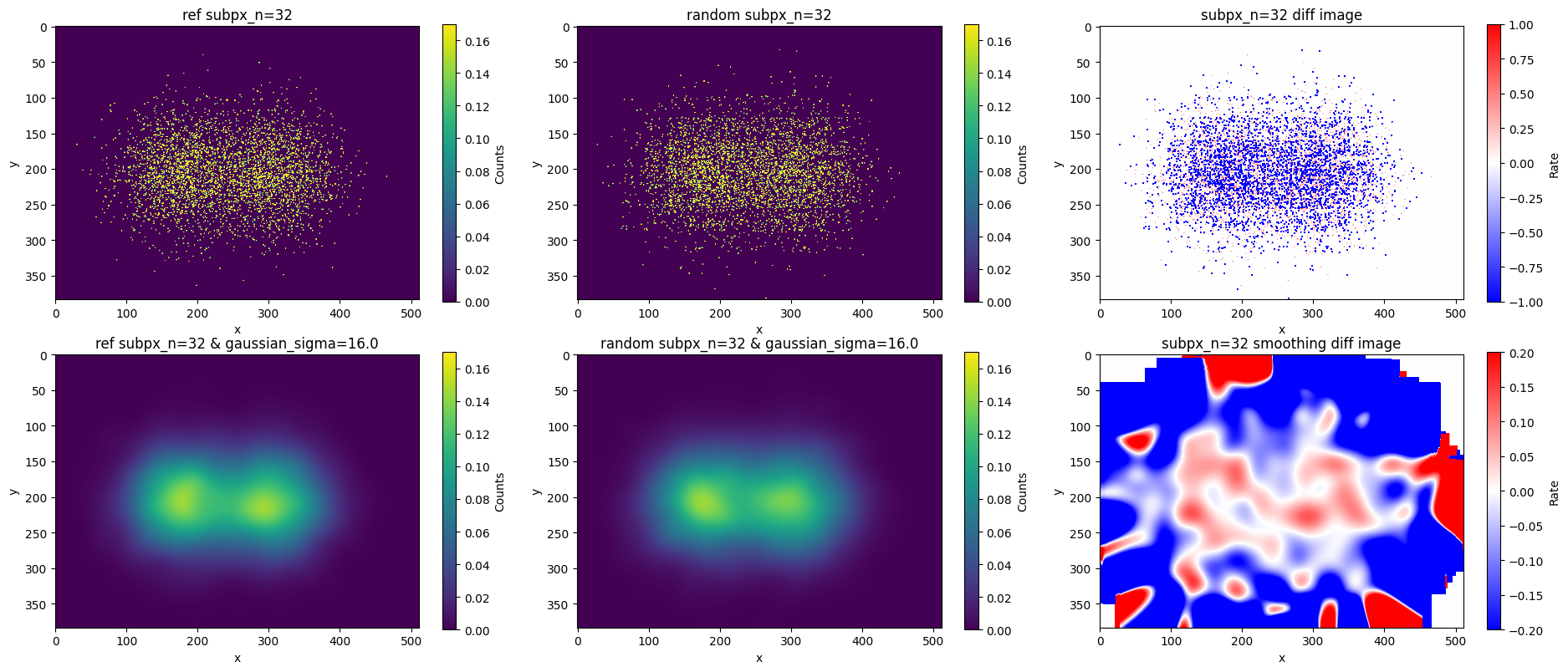
ここでは、超解像化のコードのsub_pxパラメータを変えた際の結果について見ていきます。
それぞれの下段では、ガウシアンフィルタによる平滑化のσをgaussian_sigma = sub_px / 2としていて、sub_px=1の空間スケールに平滑化しています。

下図の全ての結果において、平滑化後の下段の結果は統計誤差以内の変化率であることがわかります。

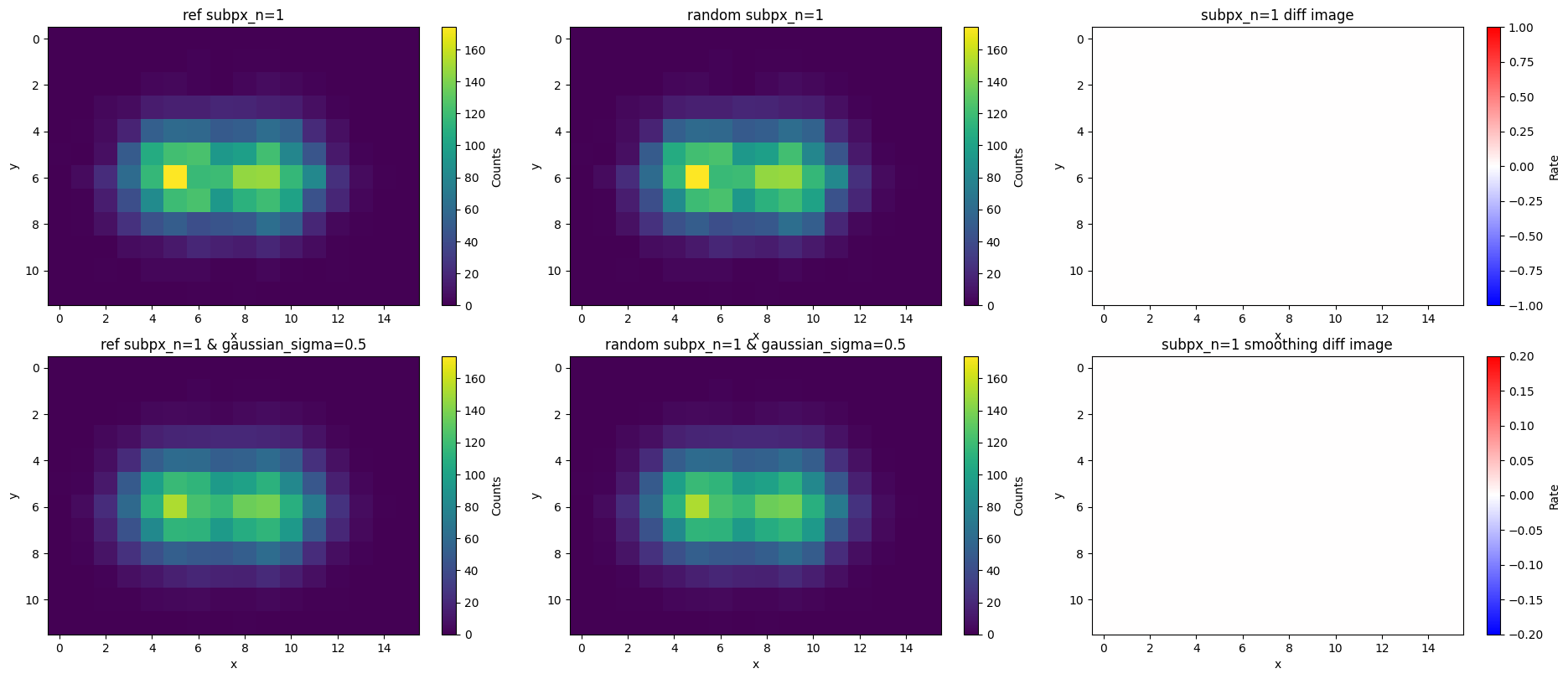
• sub_px=1の結果（もちろん、ランダム化した場合も変わらない）
  下段はgaussian_sigma = sub_px / 2より、σ=0.5のガウシアンフィルタで平滑化しているため、1ピクセルに1σ入る計算であり若干平滑化されますが、上段の構造はほとんど保持されます。他のsub_pxでの平滑化の結果は、この下段の結果に近くなるはずです。

• sub_px=2の結果
  

• sub_px=4の結果
  

• sub_px=8の結果
  

• sub_px=16の結果
  

• sub_px=32の結果
  

• sub_px=64の結果
  

• sub_px=128の結果
  

• sub_px=256の結果
  

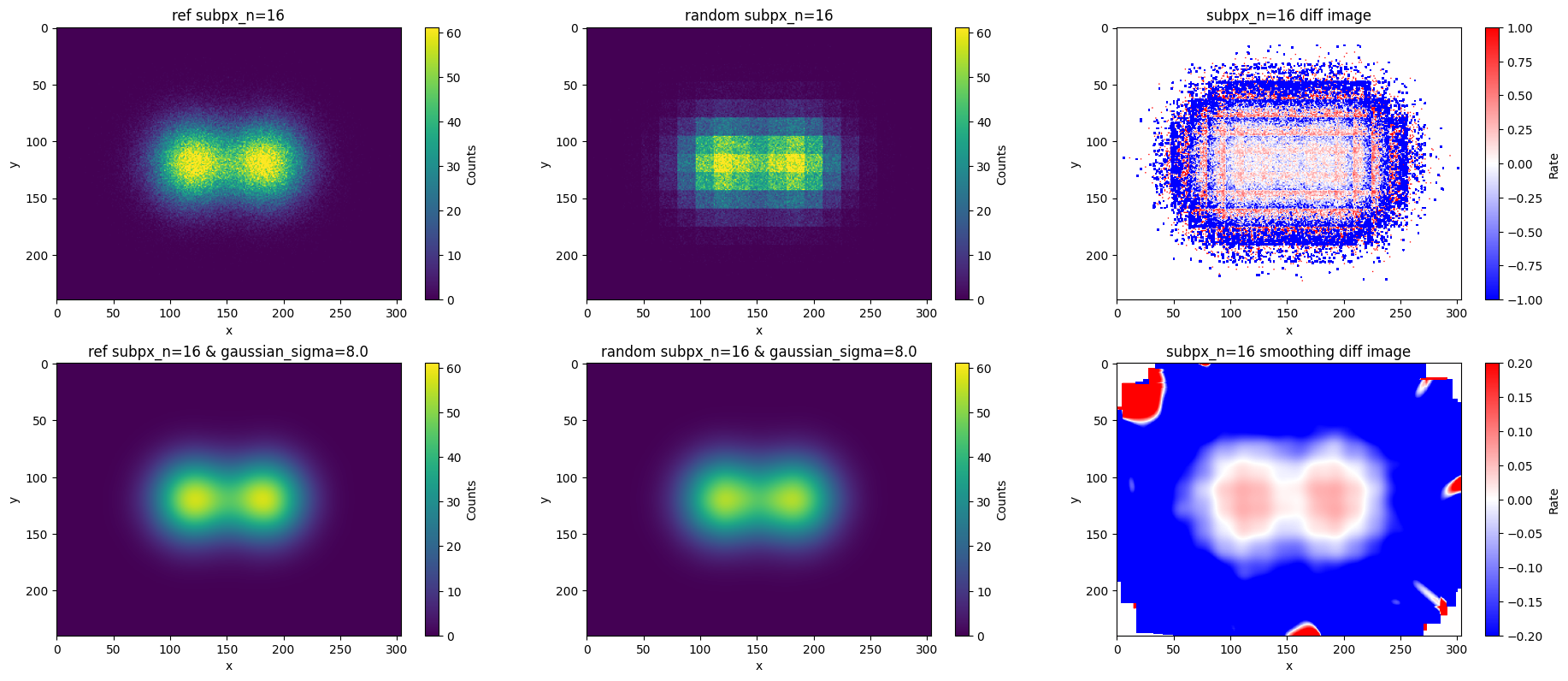
補足（ランダム化が問題となるケース）

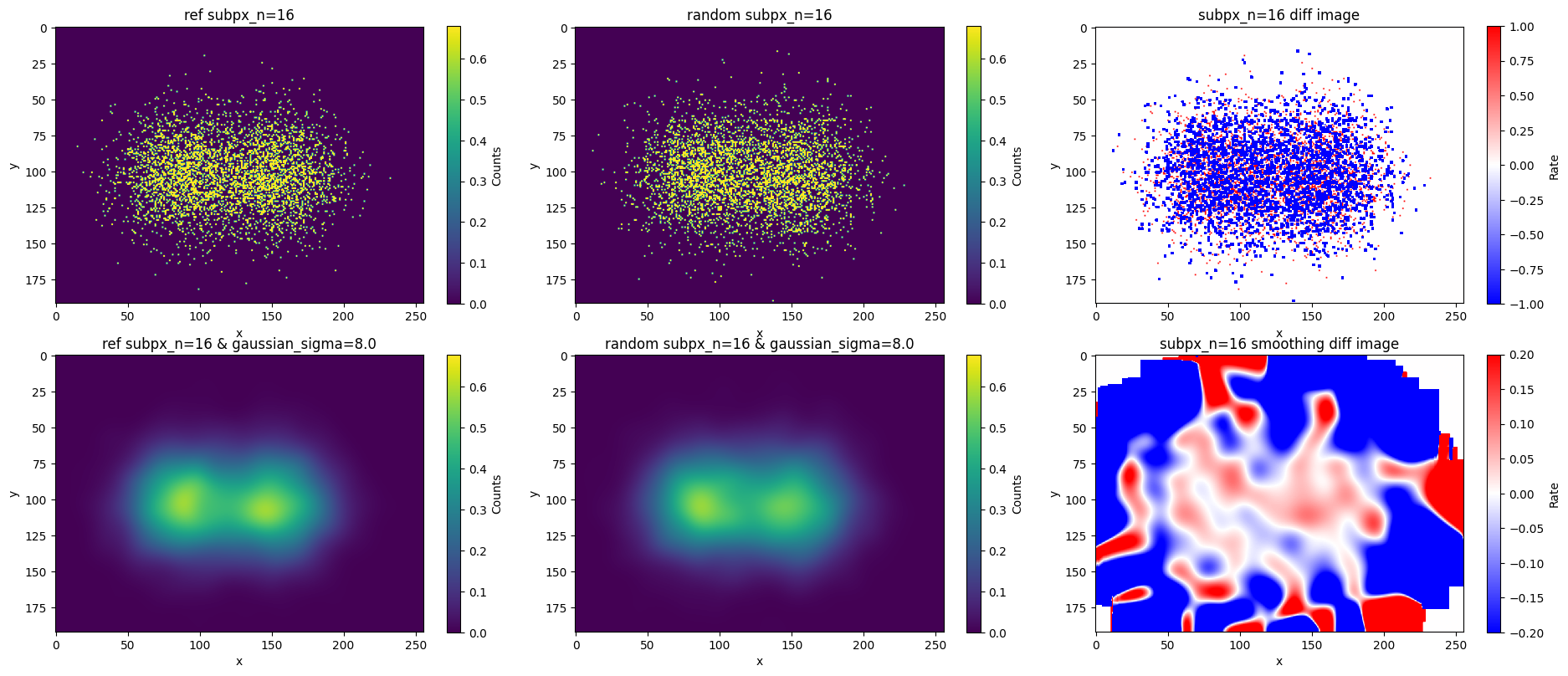
統計が多い画像において、ランダム化を用いた場合、ピクセルの境界が残ってしまうことがあります。以下は、本記事のシミュレーションで使用された画像の100倍統計量が多い例で、sub_px=16と設定した結果です。

上段左の本物の観測画像と比較して、上段中央に表示されている1×1ピクセルの観測画像を16×16にランダム化した超解像画像では、1×1ピクセルのグリッドの線が残ってしまうことが確認できます。この現象は、ランダム化に基づく一様な分布と、実際のデータの統計的な特性の違いから生じるものです。

統計量が少ない場合、この境界部は統計誤差が主要因となり、それほど目立ちませんが、本ケースでは1×1ピクセル程度のスケールでのガウシアン平滑化の重要性がより強く実感できると思います。

ランダム化の問題となるケースの実装コード

ランダム化の問題となるケースの実装コード

# 補足（ランダム化が問題となるケース）
# 2次元ガウシアン分布から乱数の散布図
np.random.seed(2023)
mean_1 = [-2, 0]
mean_2 = [2, 0]
cov = [[2, 0], [0, 2]]

# 本編のコードから100倍統計の良い画像
scale = 100
evt_x, evt_y = np.hstack([np.random.multivariate_normal(mean_1, cov, 2000*scale).T, np.random.multivariate_normal(mean_2, cov, 2000*scale).T])

# 単位目盛りあたりのグリッドを作成
x_grid = np.arange(np.floor(evt_x.min())-0.5, np.ceil(evt_x.max())+0.5001, 1)
y_grid = np.arange(np.floor(evt_y.min())-0.5, np.ceil(evt_y.max())+0.5001, 1)

# グリッド上のデータ点のカウントを計算
hist, *_ = np.histogram2d(evt_x, evt_y, bins=(x_grid, y_grid))
image = hist.T

fig, axs = plt.subplots(2, 3, figsize=(19, 8))

# リファレンス画像（散布図からスケールに合わせたグリッドで作成した元画像）
x_grid = np.arange(np.floor(evt_x.min())-0.5, np.ceil(evt_x.max())+0.5001, 1 / subpx_n)
y_grid = np.arange(np.floor(evt_y.min())-0.5, np.ceil(evt_y.max())+0.5001, 1 / subpx_n)
hist, *_ = np.histogram2d(evt_x, evt_y, bins=(x_grid, y_grid))
ref_image = hist.T

cbar = axs[0, 0].imshow(ref_image, vmin=0, vmax=image.max()/(subpx_n**2))
fig.colorbar(cbar, label='Counts')
axs[0, 0].set_title(f'ref {subpx_n=}')
axs[0, 0].set_xlabel('x')
axs[0, 0].set_ylabel('y')
axs[0, 0].set_aspect('equal')

# ランダム化によるサブピクセル化した画像を作成
subpx_n = 16
subpx_image = random_subpx(image, subpx_n)

cbar = axs[0, 1].imshow(subpx_image, vmin=0, vmax=image.max()/(subpx_n**2))
fig.colorbar(cbar, label='Counts')
axs[0, 1].set_title(f'random {subpx_n=}')
axs[0, 1].set_xlabel('x')
axs[0, 1].set_ylabel('y')
axs[0, 1].set_aspect('equal')

# リファレンス画像との差分
diff_image = (ref_image - subpx_image) / (ref_image + 1e-15)
cbar = axs[0, 2].imshow(diff_image, vmin=-1.0, vmax=1.0, cmap='bwr')
fig.colorbar(cbar, label='Rate')
axs[0, 2].set_title(f'{subpx_n=} diff image')
axs[0, 2].set_xlabel('x')
axs[0, 2].set_ylabel('y')
axs[0, 2].set_aspect('equal')

# ガウシアン平滑化パラメータ
gaussian_sigma = subpx_n / 2

# リファレンス画像のガウシアン平滑化
ref_gaussian_image = gaussian_filter(ref_image, sigma=gaussian_sigma, output=np.float64)

cbar = axs[1, 0].imshow(ref_gaussian_image, vmin=0, vmax=image.max()/(subpx_n**2))
fig.colorbar(cbar, label='Counts')
axs[1, 0].set_title(f'ref {subpx_n=} & {gaussian_sigma=}')
axs[1, 0].set_xlabel('x')
axs[1, 0].set_ylabel('y')
axs[1, 0].set_aspect('equal')

# ランダム超解像化した画像のガウシアン平滑化
subpx_gaussian_image = gaussian_filter(subpx_image, sigma=gaussian_sigma, output=np.float64)

cbar = axs[1, 1].imshow(subpx_gaussian_image, vmin=0, vmax=image.max()/(subpx_n**2))
fig.colorbar(cbar, label='Counts')
axs[1, 1].set_title(f'random {subpx_n=} & {gaussian_sigma=}')
axs[1, 1].set_xlabel('x')
axs[1, 1].set_ylabel('y')
axs[1, 1].set_aspect('equal')

# ガウシアン平滑化後のリファレンス画像との差分
diff_smoothig_image = (ref_gaussian_image - subpx_gaussian_image) / (ref_gaussian_image + 1e-15)
cbar = axs[1, 2].imshow(diff_smoothig_image, vmin=-0.2, vmax=0.2, cmap='bwr')
fig.colorbar(cbar, label='Rate')
axs[1, 2].set_title(f'{subpx_n=} smoothing diff image')
axs[1, 2].set_xlabel('x')
axs[1, 2].set_ylabel('y')
axs[1, 2].set_aspect('equal')

fig.tight_layout()
plt.show()

まとめ

本記事では、超解像化の古典的手法として比較的単純ではありますが、広く使われるランダム化について実装しました。私は2つのガウス分布から生成される画像を用いてシミュレーションを行い、その結果、統計誤差の範囲内で超解像化ができていることを確認しました。

ただし、ランダム化はピクセル毎に一様な確率分布に仮定しているため、その仮定から乖離が起こる場合に注意が必要です。その例として、空間スケール内で1ピクセル以下の細かな構造がある場合や、補足で紹介した統計が非常によく統計誤差に比べて一様分布の仮定における乖離が顕著に出る場合が挙げられます。

超解像化の方法は特定の状況に依存しますが、ランダム化はその手法の一つとして画像処理や超解像化に興味を持つ読者の皆様にとって、有益な情報となりましたら幸いです。

参考文献

Migliari, Simone, Rob Fender, and Mariano Méndez. "Iron emission lines from extended X-ray jets in SS 433: Reheating of atomic nuclei." Science 297.5587 (2002): 1673-1676.