XRISMのペルセウス銀河団のライン幅が検出器分解能よりも広がってることをPythonで確認する方法

はじめに

宇宙実験や天文学において、観測データを解析し、それに合ったモデルを作ることは、物理現象を理解する上でとても重要です。
特にX線天文学では、天体から放射されるX線スペクトルを詳しく調べることで、プラズマの温度や運動、元素の組成などがわかってきます。

本記事では、XRISM X線衛星が公開している Early Release Data を使って、X線スペクトルのフィッティング（モデルを当てはめること）を行います。対象は、ペルセウス銀河団のResolveデータ。これを Python、Xspec、PyXspec の3つの方法で解析し、それぞれの特徴や使いやすさを比べてみます。

専門的に見える内容も含まれますが、初学者向けに解析を一緒に進めていくスタイルで書いていきます。

本記事で使用するデータ

現在、XRISM 衛星の Early Release Data（初期公開データ）が一般向けに公開されており、どなたでも以下のデータにアクセスできます。

XRISM Early Release Data

本記事では、ペルセウス銀河団のResolveのデータを解析します。ペルセウス銀河団は、地球から約2億4千万光年の距離に位置する巨大な銀河団であり、X線観測によってプラズマの動きや元素組成を詳細に調べることができます。特に、XRISMの観測データには、鉄などの輝線（z, y, x, wと呼ばれるライン）が含まれており、これらのスペクトルライン幅から、100 km/s程度の視線方向の速度成分を解析することが可能です。

このデータをもとに、フィッティングを行い、ライン幅が検出器分解能よりも広がってること を確認します。

観測データ、RMF、ARFを確認

まずは、観測データ、RMF、ARFがどんなものかを可視化して確認してみましょう。

観測データの可視化

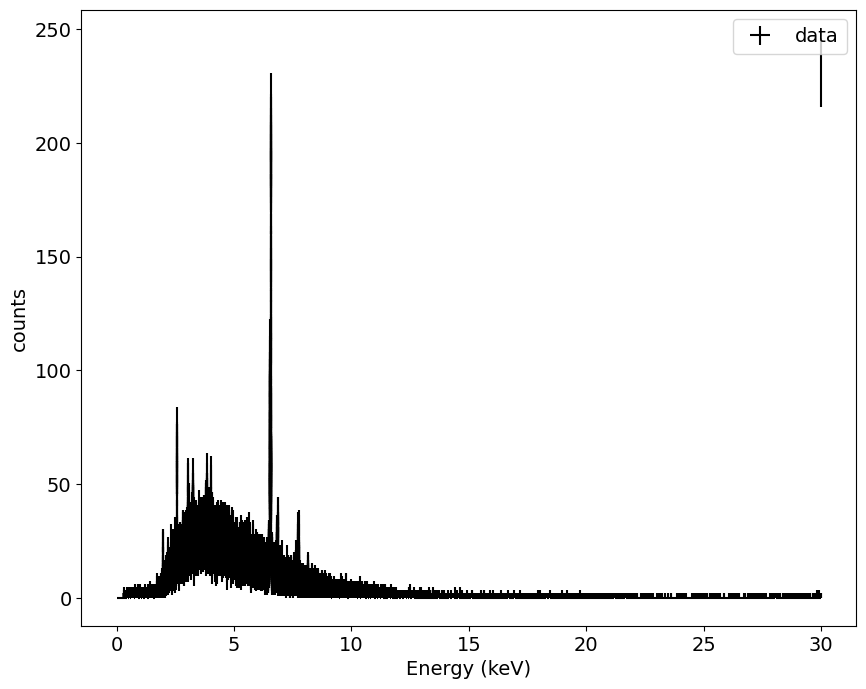
観測データ (全帯域）	6.45-6.65 keV

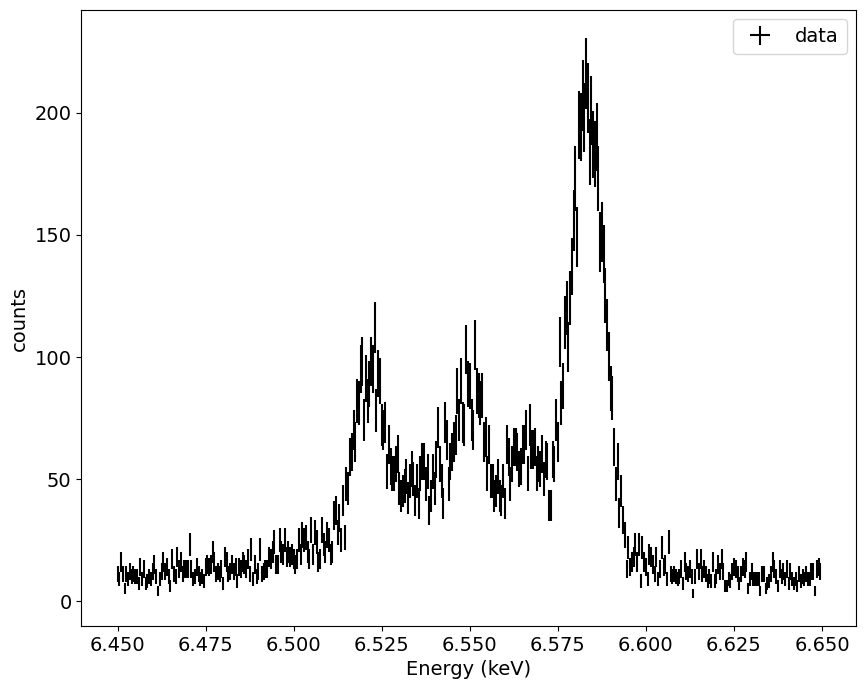この図では、横軸がエネルギー（keV）、縦軸がカウント数（検出された光子数）になっています。これが「スペクトル」と呼ばれるもので、波長やエネルギーごとに、どれだけX線が来ているかを表しています。

このスペクトルを見るときに注意したいのは、「生データがそのまま」ではないということです。実際には、観測機器の特性（応答関数）として RMF（エネルギーのずれ）や ARF（エネルギーごとの感度）を考慮する必要があります。

そこで、RMF・ARFがどんな分布なのかを確認していきます。

RMFの可視化

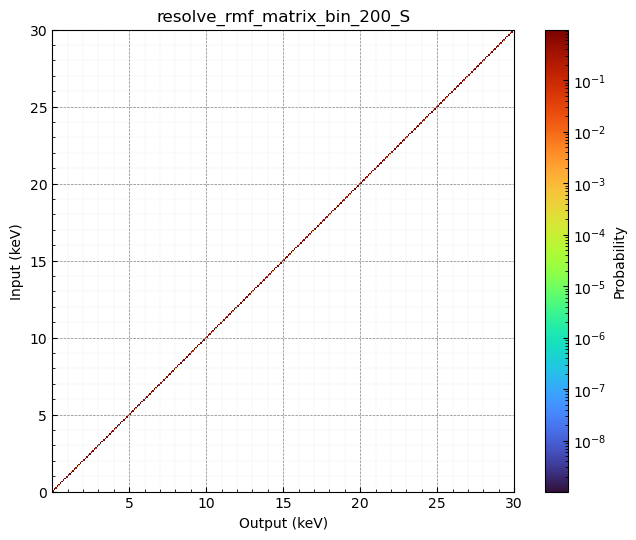
RMF (全帯域）	6.45-6.65 keV

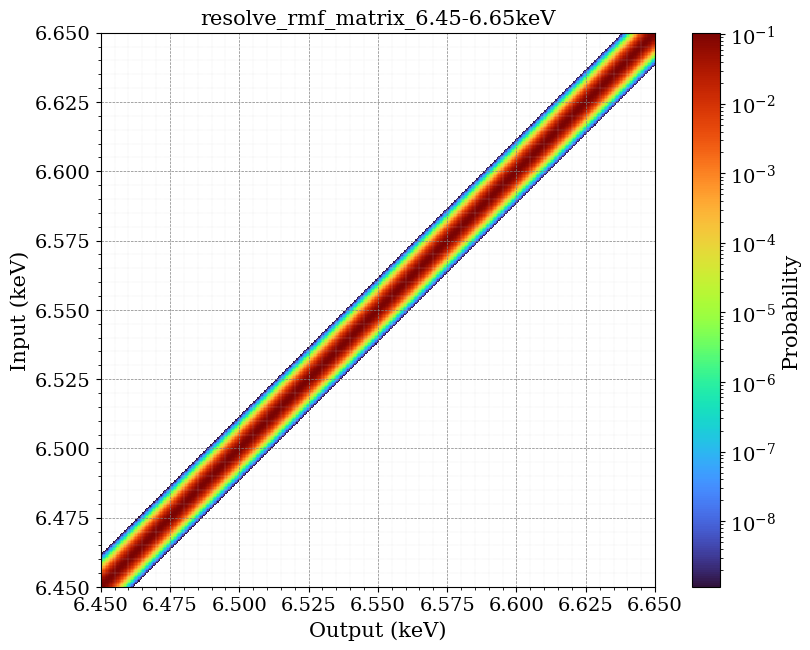RMFは縦軸の入射したエネルギーに対して横軸では出力されるエネルギーの確率分布を表しています。このように入射=出力エネルギーになるわけではなくある幅を持つことが確認できますね。

ARFの可視化

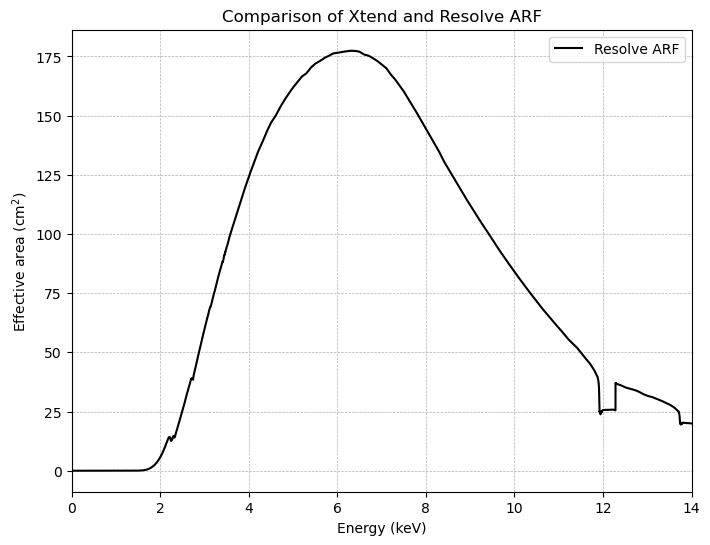
ARF (全帯域)	6.45-6.65 keV

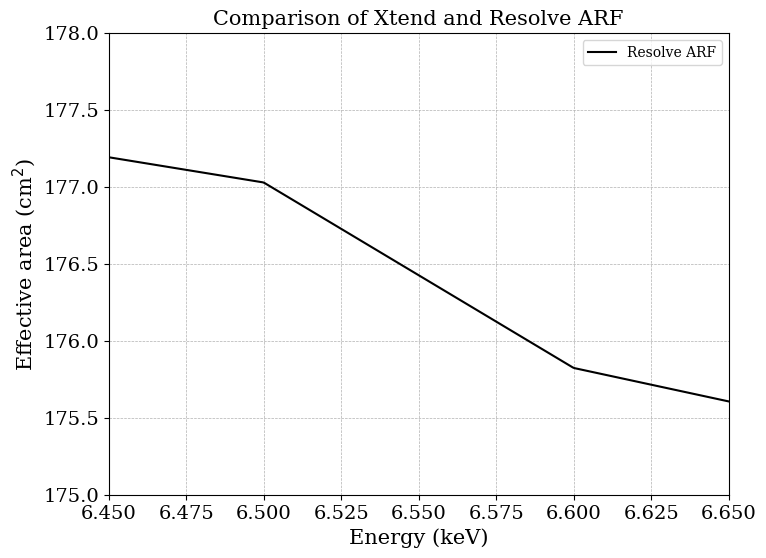ARFを見ることで、ある特定のエネルギーでは感度が高く、他では低いことを理解できます。つまりエネルギーに対して一様な放射があったしても「どのエネルギーのX線が、検出器に届きやすいか」は一様ではない、ということです。それは今回解析する6.45-6.65 keV帯域でも異なるということがわかります。

詳しくは以下の記事をご参照ください。

実装コード

RMF、ARFの描画や、Pythonで輝線幅の広がりを確認とPythonでガウシアンフィッティングの実装コードは以下から確認できます。
必要なファイルは Google Colab 上でダウンロードできるようになっていますので、そのまま実行して学習にご活用ください。
※ なお、PyXspec や XSPEC による解析は Google Colab 上での環境構築が難しいため、Google Colab 内には含めておりません。ローカル環境などでの実行をお願いいたします。

Pythonで輝線幅の広がりを確認

まずは、RMFを読み込んで実際のデータに重ねてみましょう。

Pythonで輝線幅の広がりを確認

import os
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
import astropy.io.fits as fits

plt.rcParams['font.size'] = 14

def pi_to_kev(pi):
    '''PI単位をエネルギー(keV)に変換'''
    return 1e-3 * (pi * 0.5 + 0.5)

def kev_to_pi(kev):
    '''エネルギー(keV)をPI単位に変換'''
    return int(2 * 1e3 * kev - 1)

def load_pi(infile):
    '''PIファイルを読み込み、チャンネルデータを取得'''
    with fits.open(infile) as hdul:
        pi_data = hdul[1].data
        pi_channel = pi_data['CHANNEL']
        pi_counts = pi_data['COUNTS']
    
    pi_ene = pi_to_kev(pi_channel)
    return pi_ene, pi_counts

def construct_rmf_matrix(filename):
    """
    RMFからレスポンスマトリックスを構築する関数。

    Parameters:
        filename (str): FITSファイルのパス。

    Returns:
        dict: 構築されたレスポンスマトリックスと関連データを含む辞書。
    """
    with fits.open(filename) as f:
        # 必要なデータを抽出
        f_chan = f[1].data['F_CHAN']  # チャンネルの開始位置
        n_chan = f[1].data['N_CHAN']  # チャンネルの数
        compressed_matrix = f[1].data['MATRIX']  # 密な（非ゼロのみの）マトリックスデータ
        in_ene_lo = f[1].data['ENERG_LO']  # 入力エネルギー下限
        in_ene_hi = f[1].data['ENERG_HI']  # 入力エネルギー上限
        out_ene_lo = f[2].data['E_MIN']  # 出力エネルギー下限
        out_ene_hi = f[2].data['E_MAX']  # 出力エネルギー上限

        # フルレスポンスマトリックスの次元を決定
        num_in_ene_bins = len(in_ene_lo)  # 入力エネルギーのビン数（行数）
        num_out_ene_bins = len(out_ene_lo)  # 出力エネルギーのビン数（列数）

        # フルレスポンスマトリックスを構築
        matrix = np.zeros(shape=(len(in_ene_lo), len(out_ene_lo)), dtype='float32')
        for j in range(f_chan.shape[0]):
            tot_n = 0
            for f, n in zip(f_chan[j], n_chan[j]):
                # 密なデータをフルマトリックスに埋め込む
                matrix[j, f:f + n] = compressed_matrix[j][tot_n:tot_n + n]
                tot_n += n

    return matrix, in_ene_lo, in_ene_hi, out_ene_lo, out_ene_hi

# PIファイルとRMFのパス
pi_file = 'xa_merged_p0px1000_Hp.pi'
rmf_file = 'xa_merged_p0px1000_HpS.rmf'

# データを読み込み
ene, data = load_pi(pi_file)
rmf, *_ = construct_rmf_matrix(rmf_file)

# daataのエラー
data_xerr = np.diff(ene) / 2
data_xerr = np.concatenate((data_xerr, [data_xerr[-1]]))
data_yerr = np.sqrt(data)

# 特定のエネルギーのRMFを取得
mu_z, mu_y, mu_x, mu_w = 6.521, 6.549, 6.565, 6.583
pi_z, pi_y, pi_x, pi_w = kev_to_pi(mu_z), kev_to_pi(mu_y), kev_to_pi(mu_x), kev_to_pi(mu_w)
rmf_z = rmf[pi_z]
rmf_y = rmf[pi_y]
rmf_x = rmf[pi_x]
rmf_w = rmf[pi_w]

norm_rmf_z = rmf[pi_z] / rmf[pi_z, pi_z] * data[pi_z]
norm_rmf_y = rmf[pi_y] / rmf[pi_y, pi_y] * data[pi_y]
norm_rmf_x = rmf[pi_x] / rmf[pi_x, pi_x] * data[pi_x]
norm_rmf_w = rmf[pi_w] / rmf[pi_w, pi_w] * data[pi_w]

# グラフ描画
fig, ax = plt.subplots(1, 1, figsize=(10, 8))
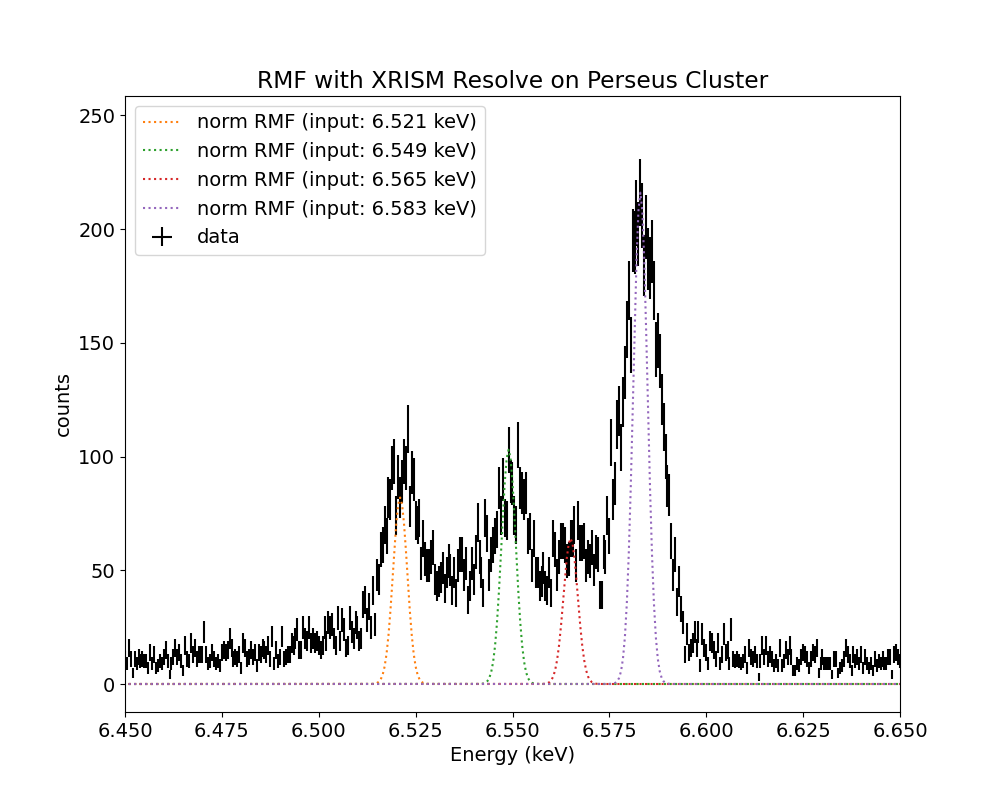
ax.errorbar(ene, data, xerr=data_xerr, yerr=data_yerr, fmt='none', label='data', color='k', linestyle='')
ax.plot(ene, norm_rmf_z, linestyle=':', color='tab:orange', label=f'norm RMF (input: {mu_z} keV)')
ax.plot(ene, norm_rmf_y, linestyle=':', color='tab:green', label=f'norm RMF (input: {mu_y} keV)')
ax.plot(ene, norm_rmf_x, linestyle=':', color='tab:red', label=f'norm RMF (input: {mu_x} keV)')
ax.plot(ene, norm_rmf_w, linestyle=':', color='tab:purple', label=f'norm RMF (input: {mu_w} keV)')
ax.set_xlabel('Energy (keV)')
ax.set_ylabel('counts')
ax.legend()
ax.set_xlim(6.45, 6.65)
ax.set_title('RMF with XRISM Resolve on Perseus Cluster')

plt.savefig('data_vs_rmf.png')
plt.show()

出力結果

観測データとRMFを重ねています。このように、RMFよりも広がっている様子を捉えることができると思います。
どのくらい広がっているのかを数値で評価するには、fittingが必要になります。

そこで次のステップとして、Pythonでガウス関数を使ってスペクトルをフィッティングしてみることにしましょう。

Pythonでガウシアンフィッティング

先ほどのデータから、直感的には4本から目を凝らしてみると5本、いや6本くらいのガウシアン成分がありそうな気もしますよね。少し定常的な成分もあるような関係が見えてきたのではないでしょうか？

とりあえず筆者は4本のガウシアン+コンスタント成分が隠れているというようにデータを捉えました。これはあくまで主観であり物的な背景を視野に入れているわけではないです。こんな感じでまずはどんなモデルが当てはまりそうかを考えながらfittingして物理的な背景を考えていくのが研究の醍醐味だと思います。

厳密にARF・RMFを畳み込んでフィットするはせず、単純にscipyのカーブフィットを使ってガウス成分でフィットします。その理由は、RMFとの畳み込みで厳密に実装するハードルが高いのと、厳密な解析はやはりXspecを活用した方が良い（Fluxの単位変換など、データ解析に必要なツールが詰まっている）ためです。

Pythonでガウシアンフィッティング

import matplotlib.pyplot as plt
import numpy as np
import astropy.io.fits as fits
from scipy.optimize import curve_fit

plt.rcParams['font.size'] = 14
def pi_to_kev(pi):
    '''PI単位をエネルギー(keV)に変換'''
    return 1e-3 * (pi * 0.5 + 0.5)

def kev_to_pi(kev):
    '''エネルギー(keV)をPI単位に変換'''
    return int(2 * 1e3 * kev - 1)

def load_pi(infile):
    '''PIファイルを読み込み、チャンネルデータを取得'''
    with fits.open(infile) as hdul:
        pi_data = hdul[1].data
        pi_channel = pi_data['CHANNEL']
        pi_counts = pi_data['COUNTS']
    
    pi_ene = pi_to_kev(pi_channel)
    return pi_ene, pi_counts

def gaussian(x, norm, mu, sigma):
    '''ガウス関数'''
    return norm * np.exp(-((x - mu) ** 2) / (2 * sigma ** 2))

def total_gaussian(ene, norm_z, norm_y, norm_x, norm_w, mu_z, mu_y, mu_x, mu_w, sigma, const):
    '''4本のガウス関数の合計'''
    return (gaussian(ene, norm_z, mu_z, sigma) +
            gaussian(ene, norm_y, mu_y, sigma) +
            gaussian(ene, norm_x, mu_x, sigma) +
            gaussian(ene, norm_w, mu_w, sigma) + const)

# PIファイルのパス
pi_file = 'xa_merged_p0px1000_Hp.pi'

# データを読み込み
ene, data = load_pi(pi_file)

# 使用するエネルギー範囲を指定
ene_min, ene_max = 6.45, 6.65
pi_min, pi_max = kev_to_pi(ene_min), kev_to_pi(ene_max)
ene = ene[pi_min:pi_max]
data = data[pi_min:pi_max]

# dataのエラー
data_xerr = np.diff(ene) / 2
data_xerr = np.concatenate((data_xerr, [data_xerr[-1]]))
data_yerr = np.sqrt(data)

# フィットの初期値
initial_guess = [110, 100, 60, 240, 6.521, 6.549, 6.565, 6.583, 0.001, 10]

# curve_fit を使ってフィッティング
popt, pcov = curve_fit(total_gaussian, ene, data, p0=initial_guess, sigma=data_yerr, absolute_sigma=True)
norm_z, norm_y, norm_x, norm_w, mu_z, mu_y, mu_x, mu_w, sigma, const = popt

# モデルデータを作成
model = total_gaussian(ene, *popt)

# グラフ描画
fig, ax = plt.subplots(1, 1, figsize=(10, 8))
ax.errorbar(ene, data, xerr=data_xerr, yerr=data_yerr, fmt='none', label='data', color='k', linestyle='')
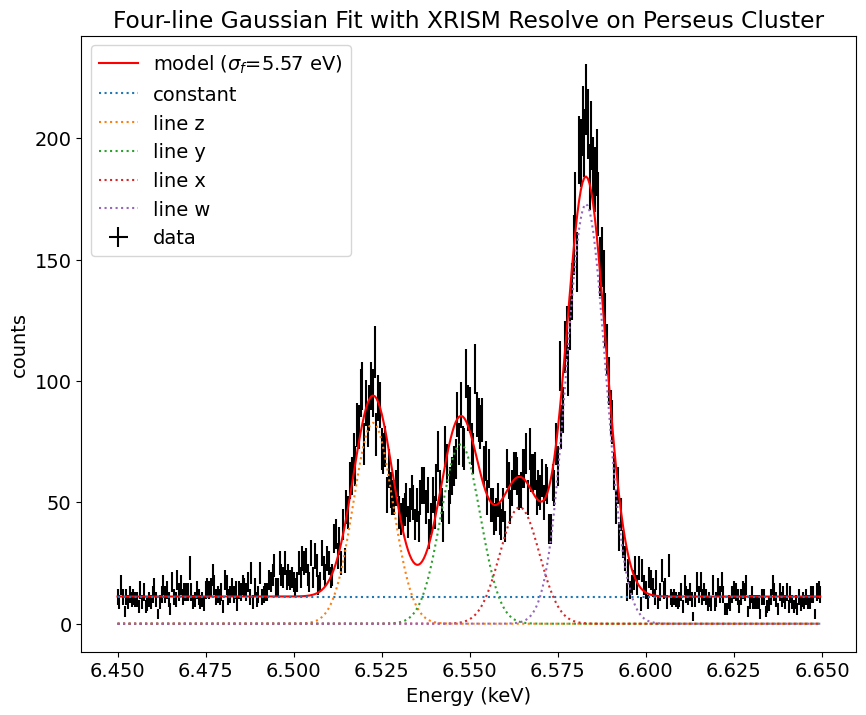
ax.plot(ene, model, color='red', label=fr'model ($\sigma_f$={sigma*1e3:.2f} eV)')
ax.plot(ene, np.full_like(ene, const), linestyle=':', label='constant')
ax.plot(ene, gaussian(ene, norm_z, mu_z, sigma), linestyle=':', label='line z')
ax.plot(ene, gaussian(ene, norm_y, mu_y, sigma), linestyle=':', label='line y')
ax.plot(ene, gaussian(ene, norm_x, mu_x, sigma), linestyle=':', label='line x')
ax.plot(ene, gaussian(ene, norm_w, mu_w, sigma), linestyle=':', label='line w')
ax.set_xlabel('Energy (keV)')
ax.set_ylabel('counts')
ax.legend()
ax.set_title('Four-line Gaussian Fit with XRISM Resolve on Perseus Cluster')

plt.savefig('fit_python.png', bbox_inches='tight')
plt.show()

出力結果

確かにガウシアンでフィットするともう少しデータを再現できました。このガウシアン幅はどれくらいあるかはフィット結果が教えてくれます。その結果は、$1\sigma_{f}=5.57~\mathrm{eV}$でした。

ここで多くの読者はこのように気づくはずです。

RMFを入れていないモデルで評価して大丈夫なのか？これは天体由来の輝線幅を表していないのでは？
→答えはYESです。

これは検出器の影響、つまり入力に対してどれくらいエネルギーが広がって検出器で観測されたかを含んだ値も含まれています。このままでは天体の輝線幅由来と検出器由来が合わさっているため、正く推定できていません。

ただし、検出器を調べると簡単な推定はできます。Resolveの検出機応答は入力エネルギーが6.5 keVのとき、FWHM$\sim4.31~\mathrm{eV}$であり、$\sigma_{rmf}\sim1.83~\mathrm{eV}$に対応します。したがって、検出器応答がガウシアン的な性質を持つとしたら、その輝線の天体由来のエネルギー幅$\sigma_{line}$は、

\sigma_{line} = \sqrt{\sigma_f^2-\sigma^2_{rmf}}\sim5.2~\mathrm{eV}

というように計算できます。しかし、ここで勘の鋭い読者はこう思うはずです。

RMFはエネルギー依存あるはずでは？これはいい加減なのでは？
→はいその通りです。鋭い視点ですね。

その通りで、このときのフィット結果にはRMFの入射エネルギーによって若干変わってくるエネルギー依存の効果は含まれていません。ですから、このままでは本来の輝線の広がり＝天体の情報を正確に読み取れていないということになります。

---

そこで、「RMFを確実に計算に取り込もう」となるわけですが、
これは畳み込み演算を計算することになり、さらにARFももちろん関わってきます。

…と、だんだん検出器まわりの話が増えてきて、
「サイエンスに入る前に、何だかもう頭がこんがらがってきそうだな」と感じた方もいるかもしれません。

でも、実はその感覚こそ、とても大切だと筆者は思います。

私たちが普段何気なく使っているPythonも、開発してくださった多くの方々の努力によって成り立っていますよね。
それと同じように、X線スペクトル解析も、観測装置を設計・開発してくださった方々や、キャリブレーション作業に尽力してくださった方々など、多くの人と技術の積み重ねの上に成り立っているのです。

だからといって、技術的背景をすべて一から理解してからでないと解析に進めないというわけではありません。
検出器の複雑さを正しく扱いながら、それでも私たちがサイエンスに集中できるように工夫された解析ツールを、感謝しながら大切に使う姿勢を持つことが大事だと、筆者は思います。

そして、そんな“一人ではとても辿り着けそうにない”解析環境を、すぐに使える形で提供してくれる頼もしいツールこそが、Xspecなんです。

Xspec編

Xspecは、RMFやARFの情報を内部で自動的に考慮しながら、スペクトルのフィッティングを行ってくれるツールです。
ユーザーは、主にコマンドを入力することで、複雑な処理を比較的簡単に実行することができます。

とはいえ、そのコマンドの数はけっこう多く、最初は少しとっつきにくいかもしれません。
そこでおすすめなのが、まずは手を動かしてコードの雰囲気に慣れることです。

以下の記事は、初学者向けにとても丁寧に書かれており、実際に動かす手順がわかりやすくまとまっていますので、あわせて参考にしてみてください。

---

Xspecを入れていることを前提としています。

xspecの入れ方は、

を参考にしてください。

Xspecの動作確認として、ターミナルでxspecとコマンドを入力してみてください。

% xspec

		XSPEC version: 12.14.0h
	Build Date/Time: Sat Jul  6 17:36:42 2024

XSPEC12>

このように立ち上がれば正常に動いています。

---

次に以下のコードを上から順にコピペして動かしてみてください。

Xspec

# データをロード
data 1:1 xa_merged_p0px1000_Hp.pi
response 1 xa_merged_p0px1000_HpS.rmf
arf 1 rsl_standard_GVclosed.arf
ignore **-6.45 6.65-**

# モデルの設定
model powerlaw + gaussian + gaussian + gaussian + gaussian
2.0
1
6.521 -1
0.001
1e-2
6.549 -1
0.001
1e-2
6.565 -1
0.001
1e-2
6.583 -1
0.001
2e-2

# シグマを共通化
newpar 7 = p4
newpar 10 = p4
newpar 13 = p4

# フィットの実行（1回目）
query yes
fit

# ラインエネルギーをフリーにして再度フィット
thaw 3
thaw 6
thaw 9
thaw 12
fit

# Xwindowの表示
cpd /xs

# 横軸をエネルギー（デフォルトは、チャンネルch）
setp e

# 一つ目をlogのdata、二つ目の(data-model)/error
# 試してみたい他の例1: pl ld ra
# 試してみたい他の例2: pl eeuf ra
pl ld delc

# モデルを応答関数で畳み込んだ成分を表示に追加
setp add

# 2軸目のセットを調整
setp com win 2
setp com log x off
setp com log y off

# 1軸目のセットを調整
setp com win 1
setp com log x off
setp com log y off
# グラフの範囲の表示範囲の調整(win 1でないと動かない？)
setp com r x 6.45 6.65

# 色を調整 (col 色ID on プロットID)
setp com col 2 on 2
setp com col 3 on 3
setp com col 4 on 4
setp com col 5 on 5
setp com col 6 on 6
# col 7(黄色) は見にくいのでcol 8 (オレンジ)を使用
setp com col 8 on 7

# プロット結果の保存
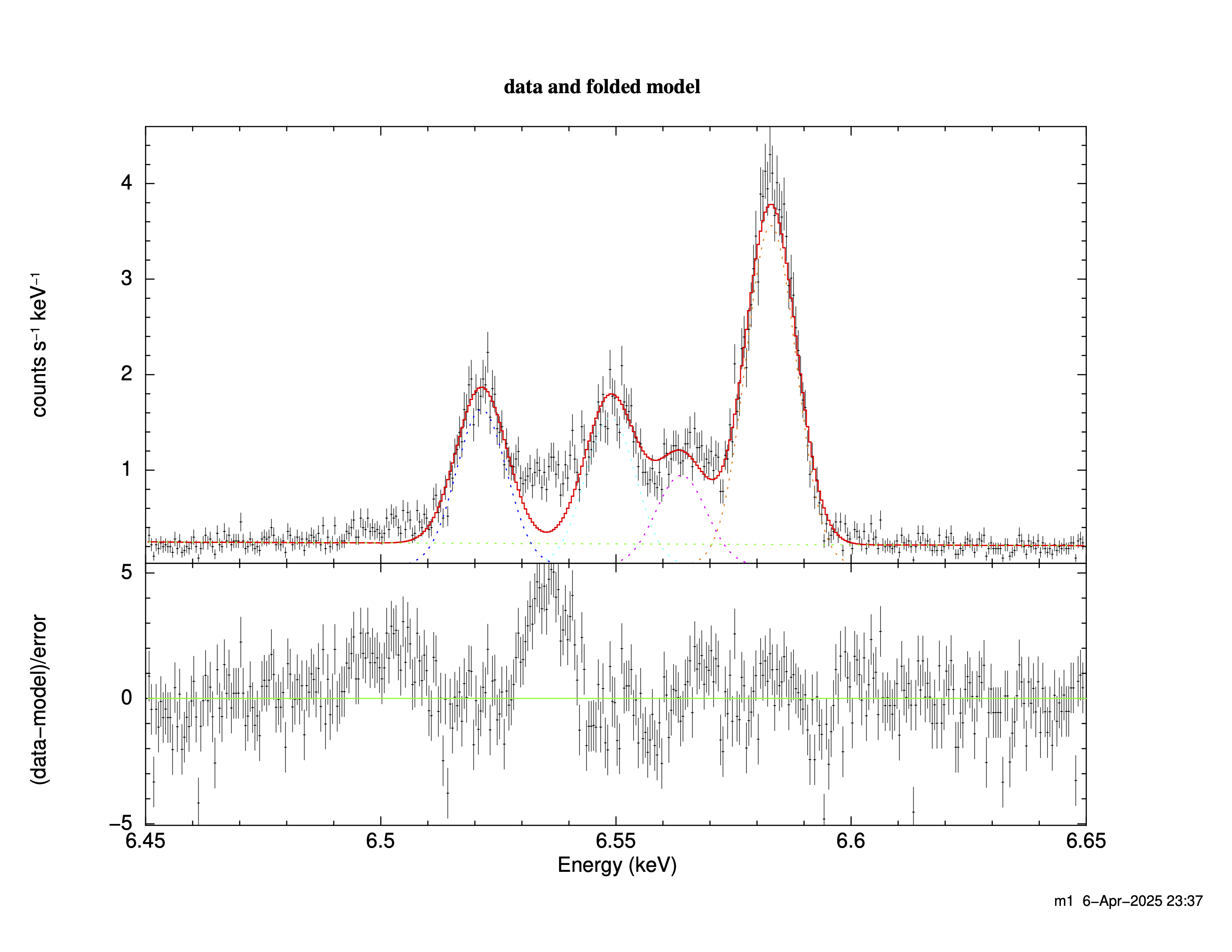
iplot
hard fit_xspec.ps/cps
we fit_xspec

# PDFに変換
# Xspecを閉じてからの方がいいかも (インタラクティブなXspec内だと動く)
ps2pdf fit_xspec.ps

fitting結果

fitting結果

========================================================================
Model powerlaw<1> + gaussian<2> + gaussian<3> + gaussian<4> + gaussian<5> Source No.: 1   Active/On
Model Model Component  Parameter  Unit     Value
 par  comp
   1    1   powerlaw   PhoIndex            5.21540      +/-  4.18495      
   2    1   powerlaw   norm                24.1612      +/-  190.292      
   3    2   gaussian   LineE      keV      6.52142      +/-  1.92014E-03  
   4    2   gaussian   Sigma      keV      5.02380E-03  +/-  6.58691E-05  
   5    2   gaussian   norm                1.28285E-04  +/-  3.66972E-06  
   6    3   gaussian   LineE      keV      6.54884      +/-  1.35229E-03  
   7    3   gaussian   Sigma      keV      5.02380E-03  = p4
   8    3   gaussian   norm                1.21878E-04  +/-  3.19095E-06  
   9    4   gaussian   LineE      keV      6.56387      +/-  2.30810E-03  
  10    4   gaussian   Sigma      keV      5.02380E-03  = p4
  11    4   gaussian   norm                7.44609E-05  +/-  2.80237E-06  
  12    5   gaussian   LineE      keV      6.58296      +/-  9.05942E-04  
  13    5   gaussian   Sigma      keV      5.02380E-03  = p4
  14    5   gaussian   norm                2.80697E-04  +/-  4.76937E-06  
________________________________________________________________________


Fit statistic  : Chi-Squared                  943.30     using 398 bins.

Test statistic : Chi-Squared                  943.30     using 398 bins.

グラフの出力結果

フィッティングのポイントとしては、まず輝線のエネルギー位置を固定しておき、安定したフィットを行ってから、その後にそれらをフリーにして再フィットするというステップを取ることです。
これは、フィッティングの収束を安定させるためのテクニックとして界隈でよく知られています。データの特徴に応じて、パラメータの初期値や範囲を適宜調整していくことも重要になります。

さて、ここで注目したいのが、フィッティングの結果として得られたsigma パラメータです。
この値は 5.02380E-03 keV（= 5.02 eV）となっており、これはRMFをきちんと考慮した上で得られた天体由来の輝線幅に相当します。
Pythonコードでおおよその見積もりを行ったときと、非常に近い結果になっていることがわかります。

---

ところで、ここまで読んだ方は「コマンドが多くて覚えるのが大変そう」「色の指定もややこしい」「PDFファイルに保存するだけでも3ステップもあるし...」と感じているかもしれません。
実際、Xspecはインタラクティブな操作を前提として作られているため、作業の再現性や自動化が少し難しい場面に遭遇することがよくあります。

そこで、筆者がよく使っているのが、Xspecの機能をそのままPythonから操作できるPyXspecというツールです。

このあとは、そのPyXspecを使って、より柔軟に・可視化しやすく・再現性のある解析を行う方法をご紹介していきます。

PyXspec編

PyXspec は、Xspecの機能をそのままPythonから使えるようにしたツールです。
特に魅力的なのが、Matplotlibでプロットできる点、スクリプトで解析を管理しやすい点です。

なお、使用にはHEASoftをソースコードからインストールする必要がある点にご注意ください（筆者は確認しておりませんが、バイナリからでは動かないかと思います）。

pyXspec

import xspec as xs
from xspec import Xset
import matplotlib.pyplot as plt
import numpy as np

# XSPECのデータをクリア
xs.AllData.clear()

# スペクトルデータの読み込み
spec = xs.Spectrum('xa_merged_p0px1000_Hp.pi', respFile='xa_merged_p0px1000_HpS.rmf', arfFile='rsl_standard_GVclosed.arf')

# 指定したエネルギー範囲を無視
spec.ignore('**-6.46 6.65-**')

# モデルの定義
model = xs.Model('powerlaw + gaussian + gaussian + gaussian + gaussian')
print('--------------------------------------------------------------')
print('Model component names:', model.componentNames)
print('--------------------------------------------------------------')

# パワーローモデルの初期パラメータ設定
model.powerlaw.PhoIndex = 2.0
model.powerlaw.norm = 1

# ガウシアンの初期パラメータ設定
model.gaussian.LineE = 6.521
model.gaussian.Sigma = 0.001
model.gaussian.norm = 1e-2
model.gaussian.LineE.frozen = True

model.gaussian_3.LineE = 6.549
model.gaussian_3.Sigma = 0.001
model.gaussian_3.norm = 1e-2
model.gaussian_3.LineE.frozen = True

model.gaussian_4.LineE = 6.565
model.gaussian_4.Sigma = 0.001
model.gaussian_4.norm = 1e-2
model.gaussian_4.LineE.frozen = True

model.gaussian_5.LineE = 6.583
model.gaussian_5.Sigma = 0.001
model.gaussian_5.norm = 2e-2
model.gaussian_5.LineE.frozen = True

# シグマパラメータをリンク
model.gaussian_3.Sigma.link = model.gaussian.Sigma
model.gaussian_4.Sigma.link = model.gaussian.Sigma
model.gaussian_5.Sigma.link = model.gaussian.Sigma

# フィットの実行（1回目）
xs.Fit.query = 'yes'
xs.Fit.perform()

# ラインエネルギーをフリーにして再度フィット
model.gaussian.LineE.frozen = False
model.gaussian_3.LineE.frozen = False
model.gaussian_4.LineE.frozen = False
model.gaussian_5.LineE.frozen = False

# フィットの実行（2回目）
xs.Fit.query = 'yes'
xs.Fit.perform()

# モデルを保存
Xset.save('fit_pyxspec.xcm')

# Matplotlibでデータをプロット
xs.Plot.device = '/null'
xs.Plot.xAxis = 'keV'
xs.Plot.add = True
xs.Plot('data delc')

# XSPECのプロットデータを取得
x_data = np.array(xs.Plot.x(1,1))
y_data = np.array(xs.Plot.y(1,1))
x_err = np.array(xs.Plot.xErr(1,1))
y_err = np.array(xs.Plot.yErr(1,1))

x_delc = np.array(xs.Plot.x(1,2))
y_delc = np.array(xs.Plot.y(1,2))
x_delc_err = np.array(xs.Plot.xErr(1,2))
y_delc_err = np.array(xs.Plot.yErr(1,2))

# ラベル情報取得
data_label = xs.Plot.labels(1)
delc_label = xs.Plot.labels(2)

y_model = np.array(xs.Plot.model())

# Matplotlibでプロット
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8), sharex=True, gridspec_kw={'height_ratios': [3, 1]})
fig.subplots_adjust(hspace=0.05)

# 観測データとモデルをプロット
ax1.errorbar(x_data, y_data, xerr=x_err, yerr=y_err, fmt='none', ecolor='k', capsize=0, label='data')
ax1.plot(x_data, y_model, color='r', label='model')

# 各コンポーネントをプロット
num_components = xs.Plot.nAddComps()
component_names = model.componentNames
for i in range(1, num_components + 1):
    y_component = np.array(xs.Plot.addComp(i))
    component_name = component_names[i - 1]
    ax1.plot(x_data, y_component, ':', label=component_name)

ax1.set_ylabel(data_label[1])
ax1.legend()

# 残差プロット
ax2.errorbar(x_delc, y_delc, xerr=x_delc_err, yerr=y_delc_err, fmt='none', ecolor='k', capsize=0, label='Data')
ax2.axhline(0, color='lime')
ax2.set_ylim(-5, 5)
ax2.set_xlabel(delc_label[0])
ax2.set_ylabel(delc_label[1])

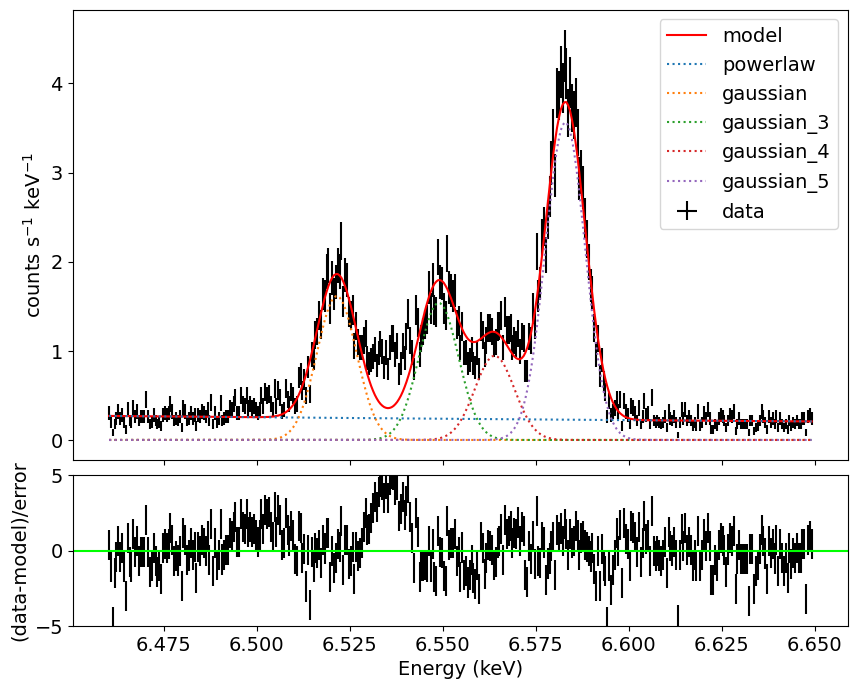
plt.savefig('fit_pyxspec.png', bbox_inches='tight')
plt.show()

出力結果

動作自体はXspecと同じです。
Matplotlibを使えばグラフのレイアウトの調整や、凡例の調整などを簡単にできるのでお勧めです。

補足まとめ：解析結果から見えたこと

今回の解析で確認できたのは、鉄の輝線（z, y, x, w）の幅が、XRISMの検出器が持つ基本の応答（RMF）よりも広くなっている点です。これは、以下のように解釈できます。

• ライン幅の拡大
  観測されたスペクトルラインは、検出器の性能による広がりだけでなく、実際の銀河団内のプラズマで生じる動き（乱流やバルク運動）によっても広がっていると考えられます。

• プラズマの動きの存在
  このラインの広がりは、プラズマが100 km/s程度の速度で動いている可能性を示しています。つまり、銀河団内部でガスが活発に動いていることが見て取れるのです。

• 解析手法の意義
  Python、Xspec、PyXspecといった複数の手法で結果を確認することで、より信頼性のあるフィッティングが行えたと考えています。各手法はそれぞれの特徴を持っており、全体として天体物理現象の理解に寄与しています。

このように、今回の解析からは、ペルセウス銀河団内部で実際にガスが動いており、その動きがスペクトルライン幅として現れていることを実際に手を動かして確認しました。

まとめ

本記事では、XRISM衛星が提供する公開データを使い、ペルセウス銀河団のX線スペクトルを「Python」「Xspec」「PyXspec」の3つの方法で解析しました。

まず、Pythonのみでもスペクトルのフィッティングは可能ですが、RMFやARFを厳密に扱うには限界があることを確認しました。次に、Xspecを使うことで、検出器の応答を含んだ本格的な解析が行えること、そしてPyXspecを用いれば、Xspecの解析をPythonで柔軟にコントロールでき、Matplotlibによる可視化やスクリプト化の利点が活かせることがわかりました。

ツールを使うだけでなく、その背後にある「誰かの努力」や「技術の積層」をほんの少し意識するだけで、解析という作業がぐっと深く、楽しくなる。そんな感覚を、この記事を通じて少しでも感じていただけたなら、筆者としてはとても嬉しい限りです。