Wiener deconvolutionをシミュレーションで理解しよう

はじめに

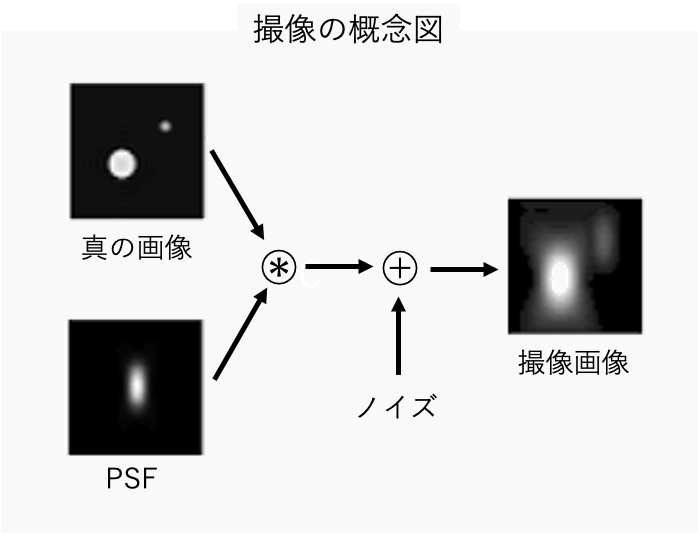
本記事では撮像画像、点拡がり関数(Point Spread Function, 以下、PSF)、ノイズの3つの情報から真の画像を推定するWiener deconvolutionと呼ばれる手法を紹介する。
一般的な撮像観測では、観測装置の回折等により光源が拡がって撮像される。この拡がり具合はPSFで表され、このPSFを考慮して真の画像を推定する手法の代表としてRL法があるが、一般的に撮像時にPSFによる拡がりの他に電気的なノイズ等が入るため、より現実的なdeconvolutionではノイズも考慮する必要がある。Wiener deconvolutionは、撮像画像、PSF、ノイズの3つの情報から真の画像を推定することができ、本記事ではグレースケール、RGB画像でのシミュレーションにより性質を理解する。

Wiener deconvolutionとは

Wiener deconvolutionとは、既知のPSFとノイズ成分と真の信号成分のS/N比、撮像画像を用いて真の画像を推定する手法である。
Wiener deconvolutionの説明は

がよくまとまっていてわかりやすく参照されたい。
この手法は撮像画像を最適化された逆フィルタ$G(u,v)$(Wiener filter)で畳み込むことで真の画像を出力する。
理論式から結果的に導かれる逆フィルタ$G(u,v)$は

G(u,v)={\frac {H^{*}(u,v)}{|H(u,v)|^{2}+\frac{N(u,v)}{S(u,v)}}}

と表される。ここで、$H(u,v)$はPSFの周波数空間領域、$S(u,v)$は真の画像の平均パワースペクトル密度、$N(u,v)$はノイズの平均パワースペクトル密度、$^*$は複素共役を表す。
一般的に、真の画像とノイズの比$N(u,v)/S(u,v)$を求めるのは困難なため定数$\lambda$で

G(u,v)=(1+\lambda){\frac {H^{*}(u,v)}{|H(u,v)|^{2}+\lambda}}

と表される。$(1+\lambda)$は、画像の輝度を一定に保つための項である。また、特にノイズが成分が0の場合は、ノイズのパワースペクトルは消失しWiener filterは単純な逆フィルター$1/H(f)$になるが、計算時は不安定になるため$\lambda=0.001$など非常に小さい値を入れておくと良い。
本記事はscikit-imageのwinerで実装するが、scikit-imageのwinerでは$N(f)/S(f)$はもう少し高級な式で

G(u,v)={\frac {H^{*}(u,v)}{|H(u,v)|^{2}+\lambda |C(u,v)|^{2}}}

と表す。ここで、$C(u,v)$は正則化演算子でデフォルトではラプラシアンフィルタが用いられる。ラプラシアンフィルタが使われる理由については以下のようである。

正則化演算子としては， ラプラシアンフィルタなどの高域通過フィルタを用いるのが一般的である. これは，以下のような理由による. 画像の電力スペクトルは低周波域に集中しており， また画像の劣化特性も多くの場合低域通過特性を持っので， 劣化画像の高周波域成分はノイズ電力がほとんどであると考えられる. したがって， 復元画像におけるノイズ成分の量を評価するためには，復元画像の高周波成分を取り出してやればよい. (渡部知樹・大木真・周欣欣・橋口住久 (1996) 「画像復元における正則化パラメータの推定」 山梨大學工學部研究報告 47, p8より引用)

実装

Google Colabで作成した本記事のコードは、こちらにあります。

本記事は真の画像をPSFで畳み込みノイズを乱数により擬似的に発生させて加えて撮像画像をシミュレーションしている。
手順については以下の通りである。

1. 真の画像(Lena画像)を入手する。Lena画像はこちらから入手できる。
2. 真の画像をPSFで畳み込む。
3. PSFで畳み込んだ画像にガウシアンノイズを加えて撮像画像を作る。
4. scikit-imageのwinerに撮像画像、PSF、S/Nの逆数の平均値、正則化演算子を使わないとき、正則化演算子4近傍ラプラシアンフィルタ、正則化演算子8近傍ラプラシアンフィルタでwiener deconvolutionする。また、比較用にscikit-imageのrichardson_Lucyを使って、撮像画像、PSFを入れてRichardson-Lucy deconvolutionする。

各種インポート

各種インポート

import cv2
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import multivariate_normal
from scipy.signal import gaussian
from skimage import restoration

実行時の各種バージョン

Name	Version
opencv-python	4.6.0.66
matplotlib	3.2.2
numpy	1.21.6
scipy	1.7.3
scikit-image	0.18.3

※scikit-imageのrestoration.richardson_lucyは、Version 0.19.1で一部変更されている。（変更箇所概要：Add small regularization to avoid zero-division in richardson_lucy (gh-5976))

PSF作成用の関数

PSF作成用の関数

def get_psf(px, sigma):
    half_px = px // 2
    x, y = np.mgrid[-half_px:half_px+1:, -half_px:half_px+1:]
    pos = np.dstack((x, y))
    mean = np.array([0, 0])  # 分布の平均
    cov = np.array([[sigma**2, 0], [0, sigma**2]])  # 分布の分散共分散行列
    rv = multivariate_normal(mean, cov)
    psf = rv.pdf(pos)
    return psf

シミュレーションに使用するPSFは何でも良いが、今回は多変量正規分布に従うPSFで実装する。多変量正規分布にはSciPyのmultivariate_normalを使用する。

グレースケール画像用の実装コード

グレースケール画像用の実装コード

# 各パラメータ
true_img_fname = 'lena.png'  # シミュレーションに使う真の画像
psf_px = 51  # PSF用のガウシアンフィルタのピクセルサイズ(奇数のみ)
psf_sigma = 7  # PSF用のガウシアンフィルタのσ
noise_sigma = 0.5  # ガウシアンノイズのσ
iterations = 50  # RL法の反復回数

# 真の画像の読み込み
true_img = cv2.imread(true_img_fname)
true_img = cv2.cvtColor(true_img, cv2.COLOR_BGR2GRAY)

# PSF
psf = get_psf(psf_px, psf_sigma)

# 真の画像をPSFで畳み込み
blur_img = cv2.filter2D(true_img, -1, psf)

# ガウシアンノイズを加えて撮像画像を作成
np.random.seed(2022)
blurNoisy_img = blur_img + np.round(np.random.normal(0, noise_sigma, true_img.shape))
blurNoisy_img[blurNoisy_img < 0] = 0
blurNoisy_img[blurNoisy_img > 255] = 255
blurNoisy_img = blurNoisy_img.astype(np.uint8)

"""deconvolution"""
balance = np.sum(np.abs(blurNoisy_img-blur_img)) / np.sum(true_img)  # S/Nの逆数を計算

# フリーエ変換後の配列数において全て1埋めすることでregを使わないwiener deconvolutionを実装
no_reg = np.ones((blurNoisy_img.shape[0], blurNoisy_img.shape[1]//2+1), dtype=np.complex64)
no_reg_wiener_img = restoration.wiener(blurNoisy_img/255., psf, balance, no_reg)
no_reg_wiener_img *= 1+balance  # deconvolution前の輝度を保つための項
no_reg_wiener_img *= 255.
no_reg_wiener_img = no_reg_wiener_img.astype(np.uint8)

# regに4近傍ラプラシアンフィルタを使用(デフォルトのreg=Noneと同一のフィルタ)
laplacian4_reg = np.array([[0, 1, 0], [1, -4, 1],  [0, 1, 0]], dtype=np.float64)
laplacian4_reg_wiener_img = restoration.wiener(blurNoisy_img/255., psf, balance, laplacian4_reg)
laplacian4_reg_wiener_img *= 255.
laplacian4_reg_wiener_img = laplacian4_reg_wiener_img.astype(np.uint8)

# regに8近傍ラプラシアンフィルタを使用
laplacian8_reg = np.array([[1, 1, 1], [1, -8, 1],  [1, 1, 1]], dtype=np.float64)
laplacian8_reg_wiener_img = restoration.wiener(blurNoisy_img/255., psf, balance, laplacian8_reg)
laplacian8_reg_wiener_img *= 255.
laplacian8_reg_wiener_img = laplacian8_reg_wiener_img.astype(np.uint8)

# 比較用にRichardson-Lucy deconvolution
rl_img = restoration.richardson_lucy(blurNoisy_img/255., psf, iterations)
rl_img *= 255.
rl_img = rl_img.astype(np.uint8)

"""表示"""
fig, axs = plt.subplots(2, 4, figsize=(28, 14))
axs[0, 0].set_title('The true image')
axs[0, 0].imshow(true_img, cmap='gray')
axs[0, 1].set_title(f'PSF psf_sigma={psf_sigma}')
axs[0, 1].imshow(psf, cmap='gray')
axs[0, 2].set_title(f'PSF convolved image')
axs[0, 2].imshow(blur_img, cmap='gray')
axs[0, 3].set_title(f'The obtained image noise_sigma={noise_sigma}(PSF convolved + noise)')
axs[0, 3].imshow(blurNoisy_img, cmap='gray')
axs[1, 0].set_title(f'Wiener deconvolution\ninverse of S/N {balance:.5f} no reg')
axs[1, 0].imshow(no_reg_wiener_img, cmap='gray')
axs[1, 1].set_title(f'Wiener deconvolution\ninverse of S/N {balance:.5f} 4-Laplacian reg')
axs[1, 1].imshow(laplacian4_reg_wiener_img, cmap='gray')
axs[1, 2].set_title(f'Wiener deconvolution\ninverse of S/N {balance:.5f} 8-Laplacian reg')
axs[1, 2].imshow(laplacian8_reg_wiener_img, cmap='gray')
axs[1, 3].set_title(f'Richardson-Lucy deconvolution\niterations={iterations}')
axs[1, 3].imshow(rl_img, cmap='gray')

plt.show()

上段左から真の画像、PSF、PSFで畳み込んだ画像、PSFで畳み込んだ後にガウシアンノイズを加えた画像(撮像画像で各deconvolutionで使った画像)である。
下段左から正則化演算子を使わないときのWiener deconvolution、正則化演算子が4近傍ラプラシアンフィルタでのWiener deconvolution、正則化演算子が8近傍ラプラシアンフィルタWiener deconvolution、Richardson-Lucy deconvolution反復回数50回の結果である。

• noise_sigma = 0.5 (ノイズ量 非常に小さい)
  

• noise_sigma = 10 (ノイズ量 小)
  
  正則化演算子が4近傍ラプラシアンフィルタでの結果(下段左から2番目)、8近傍ラプラシアンフィルタでの結果(下段左から3番目)、Richardson-Lucy deconvolutionの結果(下段左から4番目)が、ある程度ノイズを抑えてシャープな見た目になっているのがわかる。

• noise_sigma = 50 (ノイズ量 中)
  
  正則化演算子が4近傍ラプラシアンフィルタでの結果(下段左から2番目)とRichardson-Lucy deconvolutionの結果(下段左から4番目)が、ある程度ノイズを抑えてシャープな見た目になっているのがわかる。

• noise_sigma = 100 (ノイズ量 大)
  
  正則化演算子を使わないときの結果(下段左から1番目)が、ノイズを抑えていてあまりシャープになっていないがその他の3つのdeconvolutioの結果に比べて見た目が良いことがわかる。

RGB画像用の実装コード

RGB画像用の実装コード

# 各パラメータ
true_img_fname = 'lena.png'  # シミュレーションに使う真の画像
psf_px = 51  # PSF用のガウシアンフィルタのピクセルサイズ(奇数のみ)
psf_sigma = 7  # PSF用のガウシアンフィルタのσ
noise_sigma = 0.5  # ガウシアンノイズのσ
iterations = 50  # RL法の反復回数

# 真の画像の読み込み
true_img = cv2.imread(true_img_fname)
true_img = cv2.cvtColor(true_img, cv2.COLOR_BGR2RGB)

# PSF
psf = get_psf(psf_px, psf_sigma)

# 真の画像をPSFで畳み込み
blur_img = cv2.filter2D(true_img, -1, psf)

# ガウシアンノイズを加えて撮像画像を作成
np.random.seed(2022)
blurNoisy_img = blur_img + np.round(np.random.normal(0, noise_sigma, true_img.shape))
blurNoisy_img[blurNoisy_img < 0] = 0
blurNoisy_img[blurNoisy_img > 255] = 255
blurNoisy_img = blurNoisy_img.astype(np.uint8)

"""deconvolution"""
balance = np.sum(np.abs(blurNoisy_img-blur_img)) / np.sum(true_img)  # S/Nの逆数を計算

# フリーエ変換後の配列数において全て1埋めすることでregを使わないwiener deconvolutionを実装
no_reg = np.ones((blurNoisy_img.shape[0], blurNoisy_img.shape[1]//2+1), dtype=np.complex64)
no_reg_wiener_img = np.zeros_like(blurNoisy_img, dtype=np.float64)
no_reg_wiener_img[..., 0] = restoration.wiener(blurNoisy_img[..., 0]/255., psf, balance, no_reg)
no_reg_wiener_img[..., 1] = restoration.wiener(blurNoisy_img[..., 1]/255., psf, balance, no_reg)
no_reg_wiener_img[..., 2] = restoration.wiener(blurNoisy_img[..., 2]/255., psf, balance, no_reg)
no_reg_wiener_img *= 1+balance  # deconvolution前の輝度を保つための項
no_reg_wiener_img *= 255.
no_reg_wiener_img = no_reg_wiener_img.astype(np.uint8)

# regに4近傍ラプラシアンフィルタを使用(デフォルトのreg=Noneと同一のフィルタ)
laplacian4_reg = np.array([[0, 1, 0], [1, -4, 1],  [0, 1, 0]], dtype=np.float64)
laplacian4_reg_wiener_img = np.zeros_like(blurNoisy_img, dtype=np.float64)
laplacian4_reg_wiener_img[..., 0] = restoration.wiener(blurNoisy_img[..., 0]/255., psf, balance, laplacian4_reg)
laplacian4_reg_wiener_img[..., 1] = restoration.wiener(blurNoisy_img[..., 1]/255., psf, balance, laplacian4_reg)
laplacian4_reg_wiener_img[..., 2] = restoration.wiener(blurNoisy_img[..., 2]/255., psf, balance, laplacian4_reg)
laplacian4_reg_wiener_img *= 255.
laplacian4_reg_wiener_img = laplacian4_reg_wiener_img.astype(np.uint8)

# regに8近傍ラプラシアンフィルタを使用
laplacian8_reg = np.array([[1, 1, 1], [1, -8, 1],  [1, 1, 1]], dtype=np.float64)
laplacian8_reg_wiener_img = np.zeros_like(blurNoisy_img, dtype=np.float64)
laplacian8_reg_wiener_img[..., 0] = restoration.wiener(blurNoisy_img[..., 0]/255., psf, balance, laplacian8_reg)
laplacian8_reg_wiener_img[..., 1] = restoration.wiener(blurNoisy_img[..., 1]/255., psf, balance, laplacian8_reg)
laplacian8_reg_wiener_img[..., 2] = restoration.wiener(blurNoisy_img[..., 2]/255., psf, balance, laplacian8_reg)
laplacian8_reg_wiener_img *= 255.
laplacian8_reg_wiener_img = laplacian8_reg_wiener_img.astype(np.uint8)

# 比較用にRichardson-Lucy deconvolution
rl_img = np.zeros_like(blurNoisy_img, dtype=np.float64)
rl_img[..., 0] = restoration.richardson_lucy(blurNoisy_img[..., 0]/255., psf, iterations)
rl_img[..., 1] = restoration.richardson_lucy(blurNoisy_img[..., 1]/255., psf, iterations)
rl_img[..., 2] = restoration.richardson_lucy(blurNoisy_img[..., 2]/255., psf, iterations)
rl_img *= 255.
rl_img = rl_img.astype(np.uint8)

"""表示"""
fig, axs = plt.subplots(2, 4, figsize=(28, 14))
axs[0, 0].set_title('The true image')
axs[0, 0].imshow(true_img)
axs[0, 1].set_title(f'PSF psf_sigma={psf_sigma}')
axs[0, 1].imshow(psf, cmap='gray')
axs[0, 2].set_title(f'PSF convolved image')
axs[0, 2].imshow(blur_img)
axs[0, 3].set_title(f'The obtained image noise_sigma={noise_sigma}(PSF convolved + noise)')
axs[0, 3].imshow(blurNoisy_img)
axs[1, 0].set_title(f'Wiener deconvolution\ninverse of S/N {balance:.5f} no reg')
axs[1, 0].imshow(no_reg_wiener_img)
axs[1, 1].set_title(f'Wiener deconvolution\ninverse of S/N {balance:.5f} 4-Laplacian reg')
axs[1, 1].imshow(laplacian4_reg_wiener_img)
axs[1, 2].set_title(f'Wiener deconvolution\ninverse of S/N {balance:.5f} 8-Laplacian reg')
axs[1, 2].imshow(laplacian8_reg_wiener_img)
axs[1, 3].set_title(f'Richardson-Lucy deconvolution\niterations={iterations}')
axs[1, 3].imshow(rl_img)

plt.show()

• noise_sigma = 0.5 (ノイズ量 非常に小さい)
  

• noise_sigma = 10 (ノイズ量 小)
  

• noise_sigma = 50 (ノイズ量 中)
  

• noise_sigma = 100 (ノイズ量 大)
  

まとめ

本記事のPSFとガウシアンノイズでの実装の結果を表にまとめると以下のようになる。
ただし、画像の種類、PSFの大きさや種類(モーションブラーorデフォーカスブラー)、ノイズの種類(画像に相関のあるノイズorないノイズ、ホワイトノイズorガウシアンノイズorポアソンノイズ)などの条件によって結果が変わる可能性があるので注意してください。

• 入力画像のガウシアンノイズ量 非常に小さい

Deconvolutionの種類	定性的なノイズの除去度合い	定性的なブレの除去度合い	定性的な総合的な復元度合い
Wiener deconvolution正則化演算子使用なし	◎	△	△
Wiener deconvolution正則化演算子4近傍ラプラシアンフィルタ	○	◎	◎
Wiener deconvolution正則化演算子8近傍ラプラシアンフィルタ	○	○	○
Richardson-Lucy deconvolution反復回数50回	○	◎	◎

• 入力画像のガウシアンノイズ量 小

Deconvolutionの種類	定性的なノイズの除去度合い	定性的なブレの除去度合い	定性的な総合的な復元度合い
Wiener deconvolution正則化演算子使用なし	◎	△	△
Wiener deconvolution正則化演算子4近傍ラプラシアンフィルタ	△	◎	○
Wiener deconvolution正則化演算子8近傍ラプラシアンフィルタ	○	○	◎
Richardson-Lucy deconvolution反復回数50回	○	◎	◎

• 入力画像のガウシアンノイズ量 中

Deconvolutionの種類	定性的なノイズの除去度合い	定性的なブレの除去度合い	定性的な総合的な復元度合い
Wiener deconvolution正則化演算子使用なし	◎	△	○
Wiener deconvolution正則化演算子4近傍ラプラシアンフィルタ	×(色ハネあり)	○	×
Wiener deconvolution正則化演算子8近傍ラプラシアンフィルタ	○	○	◎
Richardson-Lucy deconvolution反復回数50回	△	○	△

• 入力画像のガウシアンノイズ量 大

Deconvolutionの種類	定性的なノイズの除去度合い	定性的なブレの除去度合い	定性的な総合的な復元度合い
Wiener deconvolution正則化演算子使用なし	◎	△	◎
Wiener deconvolution正則化演算子4近傍ラプラシアンフィルタ	×(色ハネあり)	△	×
Wiener deconvolution正則化演算子8近傍ラプラシアンフィルタ	○	△	○
Richardson-Lucy deconvolution反復回数50回	△	△	△

このようにガウシアンノイズが大きい画像に対しては正則化演算子を使わないWiener deconvolutionが有効で、ガウシアンノイズが少ない場合は正則化演算子は4近傍のラプラシアンフィルタかRichardson-Lucy deconvolutionが有効になるが、ノイズ成分を見積もるのが難しい場合が多いので、Richardson-Lucy deconvolutionの方が使い勝手が良いと思われる。

参考文献

• 渡部知樹・大木真・周欣欣・橋口住久 (1996) 「画像復元における正則化パラメータの推定」 山梨大學工學部研究報告 47, 6-12
• Richardson, William Hadley. 1972, JOSA, 62, 55–59
• Lucy, L. B. 1974, Astronomical Journal, 79, 745–754

参考資料