SS 433の歳差位相ゼロ点を見つめ直す：視線垂直タイミングの罠とは

歳差運動しながらジェットを吹き出すSS 433の様子（電波画像）

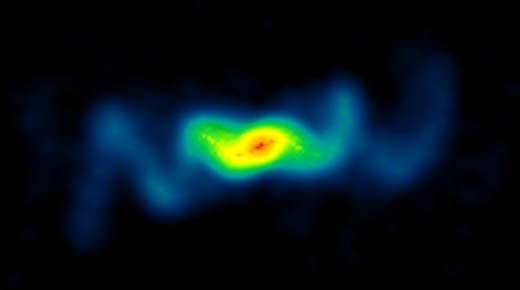
(出典: https://blackholes.stardate.org/resources/article-mystery-of-ss443.html)

はじめに

1970年代後半に発見されて以来、
40年以上にわたって多くの謎を抱え続けている奇妙なX線連星、SS 433。
この天体は、中心から高速ジェットを噴き出しながら、
ジェット軸そのものも歳差運動（precession）をしています。

歳差周期はなんと、人間のタイムスケールの約162日。
この運動により、コークスクリューのような観測画像が得られ、
また、観測される輝線のドップラーシフトにも周期的な変動が現れます。

---

文献を読み比べていると、
歳差位相のゼロ点定義が文献によって異なる
ことに気づきました。

さらに調べるうちに、
ジェットが視線に対して垂直に噴き出すタイミングを基準とする位相定義には、思わぬ罠が潜んでいる
ことが明らかになってきました。

---

こうした違いにも、
当時の事情や合理性があったのかもしれません。
歴史の中で自然に受け入れられ、使われ続けてきた背景もあるのでしょう。

しかしながら、現在の視点で改めて見直してみると、
いくつかの問題点が浮かび上がってきます。

本記事では、
視線垂直タイミングを基準とする位相定義の問題点を整理し、
なぜ現在この基準があまり使われなくなったのかについて、
筆者なりの見解をまとめました。

---

本記事の実装コードはGoogle Colabのこちらからもご覧いただけます。

SS 433の歳差運動モデル

SS 433の歳差運動の視線方向の速度成分は

\mu(\psi) = \beta[\cos i \cos\theta + \sin i \sin\theta \cos(2\pi\psi)]

ここで、

• $\beta$：ジェットの速さ（光速に対する比、$\beta \approx 0.26$）
• $\theta$：歳差円錐の半開角（約20°）
• $i$：軌道傾き（約79°）
• $\psi$：歳差位相（0〜1の周期表現）

つまり、この式はオフセット項と振幅項からなるcos関数の形をしており、歳差位相$\psi$に対して周期的に変動します。

この式の導出については

を参照してください。

モデルの位相と視線方向の速度

数式だけではイメージがつかみにくいため、ここでは簡単な概念図を用いて、東側ジェットの様子を直感的に見ていきます。
この東側ジェットは、観測者に向かって近づく方向のジェットであり、ブルージェットと呼ばれることもあります。

まず、歳差位相に対するこの式の変化をグラフに描いてみると、次のようになります。

位相と視線方向の速度の関係の実装コード

位相と視線方向の速度

import numpy as np
import matplotlib.pyplot as plt

def calc_vertical_phases(i_deg, theta_deg):
    i_rad = np.radians(i_deg)
    theta_rad = np.radians(theta_deg)

    cot_i = 1 / np.tan(i_rad)
    cot_theta = 1 / np.tan(theta_rad)
    cos_value = -cot_i * cot_theta
    cos_value = np.clip(cos_value, -1.0, 1.0)

    arccos_val = np.arccos(cos_value)
    psi_vert_1 = arccos_val / (2 * np.pi)
    psi_vert_2 = 1 - psi_vert_1

    return psi_vert_1, psi_vert_2

# パラメータ設定
beta = 0.26  # ジェットの速さ（光速に対する比）
theta_deg = 20  # 円錐半開角 [deg]
i_deg = 79      # 軌道傾き [deg]

theta = np.radians(theta_deg)
i = np.radians(i_deg)

# 視線垂直方向の速度0の時の位相
psi_vert_1, psi_vert_2 = calc_vertical_phases(i_deg, theta_deg)

# 歳差位相の範囲
psi = np.linspace(0, 1, 500)

# 視線方向速度成分 mu(psi)
mu = beta * (np.cos(i) * np.cos(theta) + np.sin(i) * np.sin(theta) * np.cos(2 * np.pi * psi))

# プロット
fig, ax = plt.subplots(figsize=(8, 5))

ax.plot(psi, mu, label=r'$\mu(\psi)$ (Blue jet)', color='blue', lw=2)
ax.axhline(0, color='gray', linestyle='--', lw=1)
ax.scatter(0, mu[0], color='k', s=80, label=r'$\psi = 0$')
ax.scatter(1, mu[-1], color='k', s=80)
ax.scatter(psi_vert_1, 0, color='tab:orange', s=80, label=rf'$\psi_\mathrm{{vert}}\approx{psi_vert_1:.2f}, {psi_vert_2:.2f}$')
ax.scatter(psi_vert_2, 0, color='tab:orange', s=80)

ax.set_xlabel(r'Precession phase $\psi$')
ax.set_ylabel(r'Line-of-sight velocity [$c$]')
ax.set_title('Line-of-sight Velocity Variation due to Jet Precession')
ax.grid(True, linestyle=':')
ax.legend()
ax.set_xlim(0, 1)
plt.tight_layout()
plt.show()

この図を見ると、$\psi=0$ の位相において、ブルージェットが観測者に最も近づくことがわかります。
また、（観測者とジェット源の相対運動を無視できると仮定すると）視線方向に対して垂直に噴き出す瞬間が、周期内に2箇所存在することも読み取れます。

ここまでくると、3次元でどんなイメージなのか気になってきますね。
せっかくなので、次節では3次元の概念図も覗いてみましょう。

---

3次元モデルの概念図

$\psi$ に依存して向きを変える単位ベクトルを3次元空間に描画することで、ジェットが放出される軌道を可視化してみます。

ブルージェットの3次元概念図（ジェット位相の回転向きや位置角は考慮していない点に注意。視線方向との角度関係は正しいが、視線に垂直な平面内での方角（位置関係）には意味を持たない。）

歳差運動の3次元概念図の実装コード

歳差運動の3次元概念図

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 歳差位相の概念図（位置角、ジェットの位相の回転方向は厳密に考慮していない）
# === パラメータ設定 ===
theta_deg = 20    # 円錐半開角 [deg]
i_deg = 79        # 円錐軸の傾き [deg]

theta = np.radians(theta_deg)
i = np.radians(i_deg)

# === 円錐の生成 ===
phi = np.linspace(0, 2*np.pi, 100)
r = np.linspace(0, 1, 50)
R, Phi = np.meshgrid(r, phi)

X = R * np.sin(theta) * np.cos(Phi)
Y = R * np.sin(theta) * np.sin(Phi)
Z = R * np.cos(theta)

# === 円錐軸の回転: x軸周りにiだけ回転 ===
def rotate_x(x, y, z, angle):
    rot_y = y * np.cos(angle) - z * np.sin(angle)
    rot_z = y * np.sin(angle) + z * np.cos(angle)
    return x, rot_y, rot_z

Xr, Yr, Zr = rotate_x(X, Y, Z, i)

# === ジェットが回る軌道（r=1の円周） ===
phi_jet = np.linspace(0, 2*np.pi, 100)
x_jet = np.sin(theta) * np.cos(phi_jet)
y_jet = np.sin(theta) * np.sin(phi_jet)
z_jet = np.cos(theta) * np.ones_like(phi_jet)
x_jet_r, y_jet_r, z_jet_r = rotate_x(x_jet, y_jet, z_jet, i)

# === 視線垂直位相の計算 ===
def calc_vertical_phases(i_deg, theta_deg):
    i_rad = np.radians(i_deg)
    theta_rad = np.radians(theta_deg)

    cot_i = 1 / np.tan(i_rad)
    cot_theta = 1 / np.tan(theta_rad)
    cos_value = -cot_i * cot_theta
    cos_value = np.clip(cos_value, -1.0, 1.0)

    arccos_val = np.arccos(cos_value)
    psi_vert_1 = arccos_val / (2 * np.pi)
    psi_vert_2 = 1 - psi_vert_1

    return psi_vert_1, psi_vert_2

psi_vert_1, psi_vert_2 = calc_vertical_phases(i_deg, theta_deg)

# phiを90度ずらしてマーク位置計算
phi_mark_0 = 2 * np.pi * (0 + 0.25)
phi_mark_1 = 2 * np.pi * (psi_vert_1 + 0.25)
phi_mark_2 = 2 * np.pi * (psi_vert_2 + 0.25)

# マーク座標計算
x_mark0 = np.sin(theta) * np.cos(phi_mark_0)
y_mark0 = np.sin(theta) * np.sin(phi_mark_0)
z_mark0 = np.cos(theta)
x_mark1 = np.sin(theta) * np.cos(phi_mark_1)
y_mark1 = np.sin(theta) * np.sin(phi_mark_1)
z_mark1 = np.cos(theta)
x_mark2 = np.sin(theta) * np.cos(phi_mark_2)
y_mark2 = np.sin(theta) * np.sin(phi_mark_2)
z_mark2 = np.cos(theta)

# 回転適用
x_mark0_r, y_mark0_r, z_mark0_r = rotate_x(x_mark0, y_mark0, z_mark0, i)
x_mark1_r, y_mark1_r, z_mark1_r = rotate_x(x_mark1, y_mark1, z_mark1, i)
x_mark2_r, y_mark2_r, z_mark2_r = rotate_x(x_mark2, y_mark2, z_mark2, i)

# === 図の作成 ===
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 円錐面
ax.plot_surface(Xr, Yr, Zr, alpha=0.3, color='cyan', edgecolor='gray', linewidth=0.5)

# ジェット軌道
ax.plot(x_jet_r, y_jet_r, z_jet_r, color='blue', lw=2, label='Blue jet orbit')

# マークをプロット
ax.scatter(x_mark0_r, y_mark0_r, z_mark0_r, color='k', s=80, label=r'$\psi = 0$')
ax.scatter(x_mark1_r, y_mark1_r, z_mark1_r, color='tab:orange', s=80, label=rf'$\psi_\mathrm{{vert}}\approx{psi_vert_1:.2f}, {psi_vert_2:.2f}$')
ax.scatter(x_mark2_r, y_mark2_r, z_mark2_r, color='tab:orange', s=80)

# Cone axis (z軸をx軸周りにi回転)
cone_axis = rotate_x(np.array([0]), np.array([0]), np.array([1]), i)
ax.quiver(0, 0, 0,
          cone_axis[0][0], cone_axis[1][0], cone_axis[2][0],
          length=1.0, color='red', linewidth=2, arrow_length_ratio=0.1, label='Cone axis')

# 視線方向 (z軸)
ax.quiver(0, 0, 0,
          0, 0, 1,
          length=0.7, color='black', linestyle='--', linewidth=2, arrow_length_ratio=0.1, label='Line of sight')


ax.set_xlim([-0.6, 0.6])
ax.set_ylim([-0.6, 0.6])
ax.set_zlim([-0.6, 0.6])
ax.set_box_aspect([1, 1, 1])

ax.view_init(elev=0, azim=45)  # 視点の角度調整
ax.set_title('Precessing Jet Structure and Vertical Phases of SS 433')
ax.legend()
plt.tight_layout()
plt.show()

ジェットは、円錐面をなぞるように動いています。
イメージとしては、園芸用ホースから水を噴き出しながら、
手元を固定して円錐状に回すと、
水が斜めに広がる円を描きながら飛んでいく——そんな感じです。

この動きを視線方向から見ると、まるで水が螺旋を描いているように見えるでしょう。
（※実際の水流では重力による垂れ下がりもありますが、ここではイメージのため無視しています。）

そして、それがまさにこの記事の冒頭に載せた観測画像に対応しているのです。

次節では、この視線垂直に吹き出す特別なタイミングについて、数式を使って整理していきます。

ジェットが視線に垂直に噴き出す瞬間とは？

SS 433では、ジェットが視線方向に対して垂直に噴き出すタイミングが周期的に現れます。
なぜここでこの瞬間を導出するかというと、
このタイミングを歳差位相の基準点として定義する流儀が存在するためです。

そこでここでは、ジェットが視線に垂直になる位相について、数式を用いて整理してみましょう。

この条件は単純で、視線方向の速度成分 $\mu(\psi)$ がゼロになる瞬間に対応します。
数式で表すと、

\mu(\psi_\text{vert}) = v[\cos i \cos\theta + \sin i \sin\theta \cos(2\pi\psi_\text{vert})] = 0

となります。

この式を解くと、

\begin{align}
v[\cos i \cos\theta + \sin i \sin\theta \cos(2\pi\psi_\text{vert})] &= 0 \\
\iff \cos(2\pi\psi_\text{vert}) &= -\frac{\cos i \cos\theta}{\sin i \sin\theta} \\
\iff \cos(2\pi\psi_\text{vert}) &= -\cot i \cot\theta
\end{align}

となります。

ここで$\cos x = a$は区間$[0, 2\pi)$において$x,~2\pi-x$の2解を持つため、
$\psi_\text{vert}$は次の2つの値になります。

\psi_\text{vert}
= 
\begin{cases}
 \displaystyle \frac{1}{2\pi}\arccos\bigl(-\cot i\cot\theta\bigr),\\[1ex]
 \displaystyle 1 - \frac{1}{2\pi}\arccos\bigl(-\cot i\cot\theta\bigr)
\end{cases}

例えば、$i=79^\circ$, $\theta=20^\circ$を代入すると、$\psi_\text{vert} \approx 0.34$ と $0.66$ が得られます。

視線垂直タイミングを計算する確認コード

視線垂直タイミングの確認

import numpy as np

def calc_vertical_phases(i_deg, theta_deg):
    i_rad = np.radians(i_deg)
    theta_rad = np.radians(theta_deg)

    cot_i = 1 / np.tan(i_rad)
    cot_theta = 1 / np.tan(theta_rad)
    cos_value = -cot_i * cot_theta
    cos_value = np.clip(cos_value, -1.0, 1.0)

    arccos_val = np.arccos(cos_value)
    psi1 = arccos_val / (2 * np.pi)
    psi2 = 1 - psi1

    return psi1, psi2

psi1, psi2 = calc_vertical_phases(79, 20)
print(f'{psi1:.4f}, {psi2:.4f}')  # 出力: 0.3397, 0.6603

視線垂直タイミング基準の「罠」

この記事で伝えたい本質的な問題点は、次の2つです。

（1）パラメータ依存でゼロ点が動く

視線垂直タイミングの位相 $\psi_{\text{vert}}$ は、傾き角 $i$、半開角 $\theta$ に依存します。

つまり、
このタイミングを位相0と決めても、パラメータが違えばゼロ点も動いてしまう。

ゼロ点の管理が煩雑になり、論文ごとに補正や調整が必要になってしまいます。

---

（2）1周期に2回現れる

また、このタイミングは1周期内に2回（$\psi_\text{vert} \approx 0.34,~0.66$）現れます。

どちらを位相0にするかが曖昧になり、混乱を招きやすくなります。

なぜ「ブルージェットがこちらに最も近づく瞬間」を基準とすると良いのか？

このような問題点を踏まえると、

• パラメータ（$i$, $\theta$）に依存しない
• 1周期に1回だけ現れる

といった性質を持つ基準が望ましく思えてきます。

そこで、
ブルーシフト側のジェット（東ジェット）が観測者に最も向かう瞬間
すなわち$\psi=0$を基準とする定義が、現代では主流となっています。

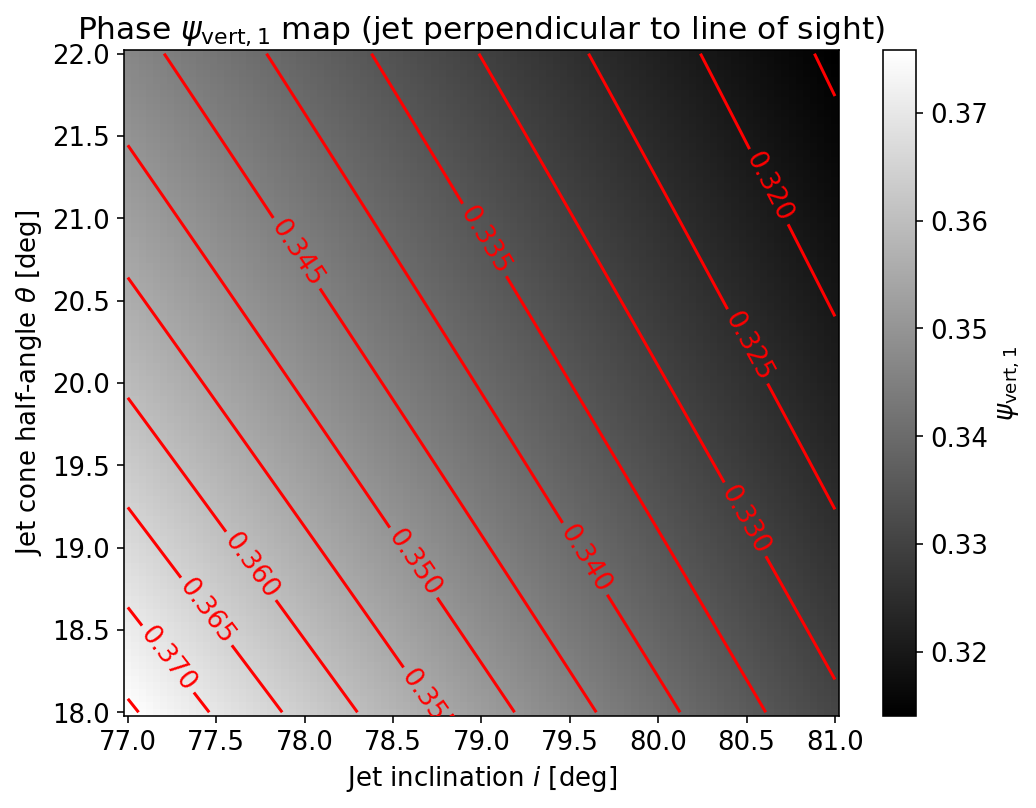
Pythonで可視化する視線垂直タイミングの揺らぎ

視線垂直タイミングの位相 $\psi_\text{vert}$ が、傾き角 $i$ や半開角 $\theta$ にどう依存するかを把握しておくことは、
文献を正しく読み解くための重要な鍵になると筆者は考えています。

そこで、Pythonを使って簡単に可視化してみましょう。

位相 $\psi_\text{vert}$ には通常2つの解が存在しますが、
ここでは0.5以下に現れる片側の解のみに注目します。

視線垂直タイミング位相 $\psi_\text{vert}$ の $i$, $\theta$ 依存性

import numpy as np
import matplotlib.pyplot as plt

def calc_vertical_phases(i_deg, theta_deg):
    i_rad = np.radians(i_deg)
    theta_rad = np.radians(theta_deg)

    cot_i = 1 / np.tan(i_rad)
    cot_theta = 1 / np.tan(theta_rad)
    cos_value = -cot_i * cot_theta
    cos_value = np.clip(cos_value, -1.0, 1.0)

    arccos_val = np.arccos(cos_value)
    psi1 = arccos_val / (2 * np.pi)
    psi2 = 1 - psi1

    return psi1, psi2

# パラメータ範囲
i_values = np.linspace(77, 81, 100)
theta_values = np.linspace(18, 22, 100)
I, Theta = np.meshgrid(i_values, theta_values)

Psi_vert_1 = np.zeros_like(I)

for idx_i in range(I.shape[0]):
    for idx_j in range(I.shape[1]):
        psi1, _ = calc_vertical_phases(I[idx_i, idx_j], Theta[idx_i, idx_j])
        Psi_vert_1[idx_i, idx_j] = psi1

# 可視化
fig, ax = plt.subplots(figsize=(8, 6))
c = ax.pcolormesh(I, Theta, Psi_vert_1, shading='auto', cmap='gray')
fig.colorbar(c, ax=ax, label=r'$\psi_\mathrm{vert,1}$')

# 等高線を引く
levels = np.arange(0.30, 0.38, 0.005)
contour = ax.contour(I, Theta, Psi_vert_1, levels=levels, colors='red')
ax.clabel(contour, fmt={lv: f'{lv:.3f}' for lv in levels}, inline=True)

ax.set_xlabel(r'Jet inclination $i$ [deg]')
ax.set_ylabel(r'Jet cone half-angle $\theta$ [deg]')
ax.set_title(r'Phase $\psi_\mathrm{vert,1}$ map (jet perpendicular to line of sight)')

plt.show()

出力結果

このように、視線垂直タイミングの位相 $\psi_\text{vert}$ が、$i$、$\theta$に応じて変化する様子がわかります。

補足：歳差位相のゼロ定義は実は3パターンある

なお、歳差位相のゼロ点の定義には、他にもいくつかのバリエーションがあります。

代表的なものをまとめると、以下の通りです。

ゼロの基準	位相 $\psi$
東ジェットの視線方向の速度成分が最大	0
西ジェットの視線方向の速度成分が最大	0.5
ジェットが視線に対して垂直に噴き出すタイミング	約0.34 または 約0.66

文献を読む際には、「どの基準で位相が定義されているか」を必ず確認することが重要です。
一見似ていても、ゼロ点の置き方ひとつで解釈が大きく変わってしまうことがあります。

文献紹介

SS 433の歳差運動に関する数式の説明は、以下の論文がわかりやすいので、参考にしていただければと思います。

この文献の式(10)において、視線垂直タイミングの位相を計算しています。

おわりに

歴史を完全に遡ることは、ほとんど不可能だと認めざるを得ません。
知らず知らずのうちに、数多くの定義が生まれ、
再解釈され、あるいは静かに姿を消していきました。
そして、今に残る定義もまた、必ずしも最適だったとは限らず、
ときには単なる慣習として、受け継がれているにすぎないものもあります。

そんな中で、ふと気づく「わずかなブレ」。
そのブレを、少しでも鮮明に捉え直したい——
そんな願いが、
物理現象に共通のものさしを与え、
歴史を紡いできたのでしょう。

移ろう定義を結び直すことばを添えることは、
人類の知を、確かに未来へとつなぐリレーなのです。

この記事が、そのバトンの一部になれたのなら、
その握り方に、一切のこだわりはありません。