概要
ふたつの線が交差しているとはどういうことなのか、アルゴリズムを作ってコンピュータに判定させてみる。
はじめに
MIERUNEの鈴木です。世間ではもうすぐクリスマスが到来しますが、私が普段通ってるゲームの世界では、どうも街に大量のサーモンが到来する異常事態が発生してるようです。なんのことだか。
それはさておき、今回のアドベントカレンダー記事は「計算幾何学」の話を書いてみます。
計算幾何学って?
計算幾何学は平面や空間上の図形を扱った問題とその解法を研究する学問です。
ちなみに「けいさんきかがく」という読みを聞いただけだと、聞いた人は「計算機科学」と勘違いしがちだとか。計算幾何学自体も計算機科学のテリトリーに含まれるのがややこしい。
計算幾何学で扱う問題は多岐にわたっており、その研究のおかげで、コンピュータを用いた設計のCAD/CAM、コンピュータゲーム、そして、弊社MIERUNEの主な業務であるGISなどの応用分野が成り立っており、これらを普段利用・活用してる私たちは、計算幾何学さまに足を向けて寝られないと言えます。
今回のアドベントカレンダーのネタで、計算幾何学を調べてみようと思いついたのはいいとして、学生の頃に情報学を学んだものの、どっちかというと文系寄りの私にとって計算幾何学はちょっと難しい。
そんなわけで今回は、こんな私でも理解できた、線の交差を判定するアルゴリズムについて書いてみようと思います。
線同士の交差判定:線分交差判定
線同士の交差判定することは、線分交差判定問題とよばれてるそうです。
人間は目で見ることで線同士が交差してることがすぐわかりますが、機械に判定させる場合、機械には目がついてないので判定には計算が必要になります。(最近のコンピュータはカメラがついてるじゃん…という野暮なツッコミは禁止です)
交差を計算させることができれば、人の目だと判別が困難な、重なってるのかどうか一見わからない線なんかについても、機械なら楽に判定できるはず。
線が交差した状態とは?
ということで、線の交差について考えていきます。
ある平面上に存在する点A・Bを結ぶ線分AB、点C・Dを結ぶ線分CDがあったとします。
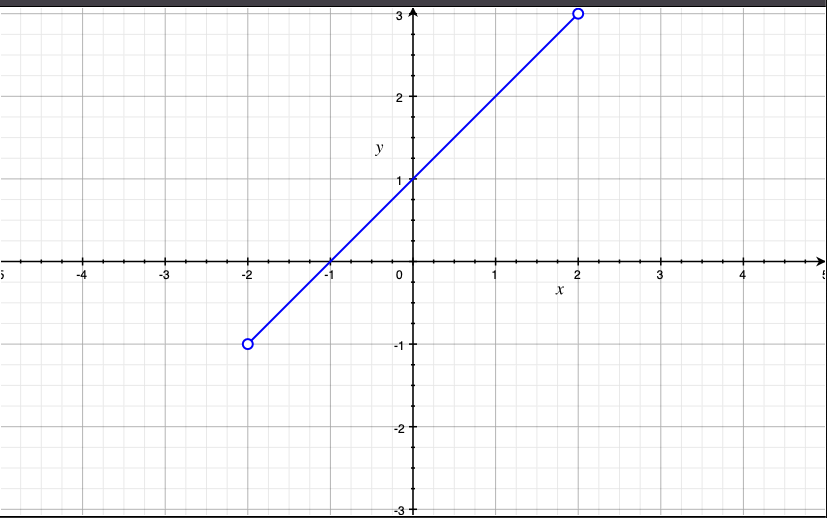
線分ABのグラフ
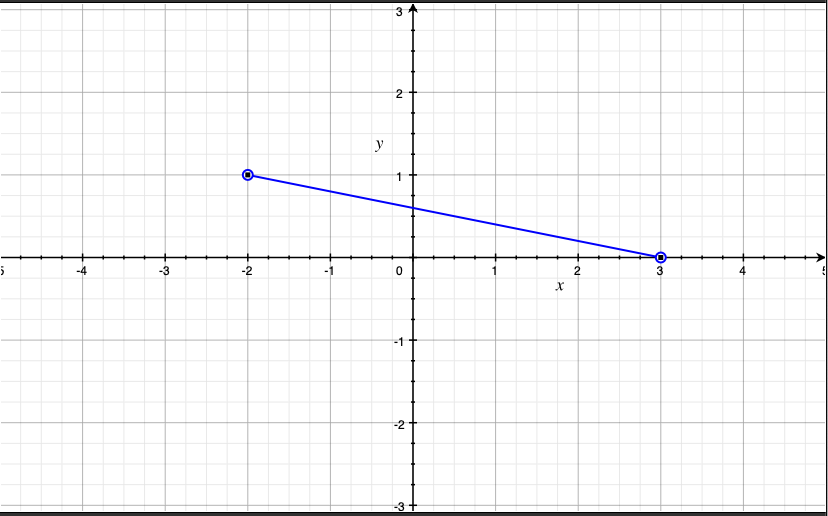
線分CDのグラフ
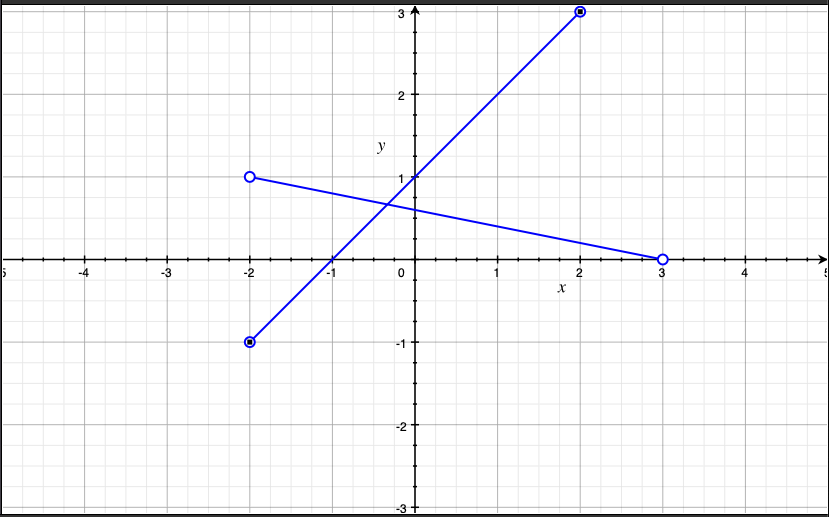
線分AB, CDを重ねたグラフ。
これらの線分ABとCDが交差してるかを確認するには、線分ABからみた場合、
- 線分ABを果てしなく伸ばし、平面を分割する直線を作る
- 線分CDの端点である点C・Dが、線分ABを含んだ直線によって平面を分割した領域それぞれに存在する
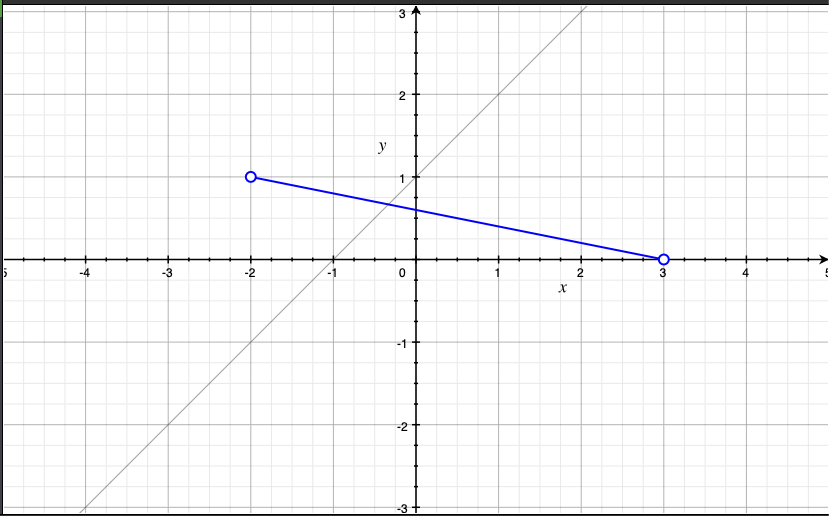
ということになりそうです。グラフに描いてみると、こんな感じですね。
交差を判定する計算式
線の交差の条件は定義できましたが、アルゴリズムを作るためには、この状態を算出するため何かしら計算式を作る必要があります。
一次関数で交差を判定してみる
グラフに線を描くといえば、中学校の数学の時間で習った一次関数が使えそうです。
$y=ax+b$ というやつです。aは傾き、bは切片ですね。
さきほど線が交差してる状態を
- 線分ABを果てしなく伸ばし、平面を分割する直線を作る
- 線分CDの端点である点C・Dが、線分ABを含んだ直線によって平面を分割した領域それぞれに存在する
と定義しましたが、実際に座標値を設定して検証してみましょう。
線が交差してる場合の検証
まずは点ABCDを用意します。
- 点Aの座標 $(-2, -1)$
- 点Bの座標 $(2, 3)$
- 点Cの座標 $(-2,1)$
- 点Dの座標 $(3,0)$
点A,Bを端点にとる線分 AB を含む一次関数 $y=ax+b$ の式を、端点ABの座標から求めてみます。
傾きaは、$\frac{(yの増加量)}{(xの増加量)}=\frac{(y2-y1)}{(x2-x1)}$で求められるので、座標A, Bの値を当てはめ
$\frac{(3-(-1))}{(2-(-2))} = \frac{4}{4} = 1$
ということで、a=1。
切片b は一次関数から、 $b = y - (a*x )$
で求められるので、座標Aと傾きaの値を当てはめ
$b = -1 - (1*-2) = -1 + 2 = 1$
ということで、b=1。
これらの値を一次関数 $y=ax+b$ に当てはめると
$y=x+1$
となりました。これを一次関数の一般形 $ax+by+c=0$ にするため、移項すると
$x-y+1=0$
となります。
一般形の式に点Aの座標を適用してみると、
$-2-(-1)+1=0$
次に点Bの座標を適用してみると、
$2-3+1=0$
となります。
さらに、線分ABの一次関数・一般形の式に点C、点Dの座標を当てはめてみると
点Cの場合、
$-2-1+1 = -2$
点Dの場合、
$3-0+1 = 4$
となります。
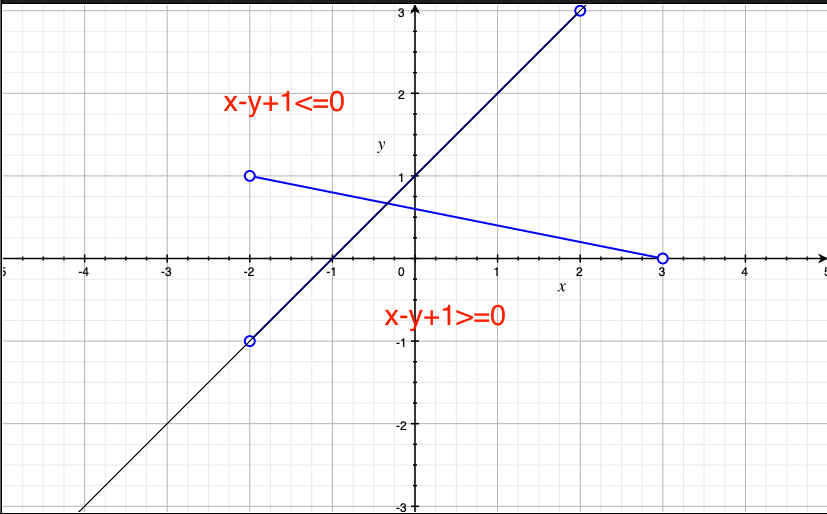
どうやら線分ABを含む一次関数に対し、点Cの座標を当てはめたときは負の値、点Dの座標の方は正の値が得られました。この状態のとき線が交差してるとみなせそうです。
グラフに描いてみるとこんな感じになります。
線が交差してない場合の検証
線同士が交差してないケースについても検証してみます。
点E,Fを定義
- 点Eの座標 $(-1, -2)$
- 点Fの座標 $(3,-1)$
点E, Fを端点とする線分EFについて、線分ABを含む一次関数のに、端点の座標を当てはめてみると、
端点Eの場合、
$-1-(-2)+1=2$
端点Fの場合、
$3-(-1)+1=5$
ということで、どちらも正の値になりました。
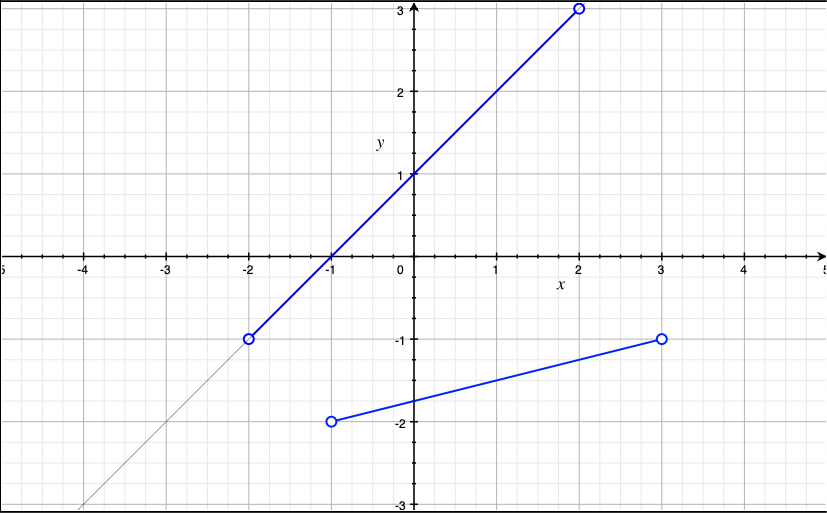
グラフで見てみるとこのようになります。目視でも線分ABと線分EFは交差してません。
ということである線に別の線が交差してることを確認するには、ある線分を含んだ一次関数に対し、交差判定させる線分の端点二箇所の座標を当てはめて、正の値・負の値どちらも現れた場合に交差してるとみなせそうです。
実装
ということで線が交差の定義と計算式がわかったので、実装を行ってみたいと思います。
今回の交差判定手法は平面上の座標に対して有効で、GISで扱う測地系・投影法の座標に対して用いた場合、ズレが生じるためか想定した結果が出てきません。
ということで、Pythonで平面幾何を扱うことのできる sympy ライブラリを使って、実装と動作確認をしてみます。
from sympy import geometry
import matplotlib.pyplot as plt
def my_intersects(geom1, geom2):
point1 = geom1.p1 # チェック元線分の端点1
point2 = geom1.p2 # チェック元線分の端点2
point3 = geom2.p1
point4 = geom2.p2
# geom1 の座標情報から、傾きと切片を求める
a = (point1[1]-point2[1]) / (point1[0]-point2[0])
b = point1[1] - (a * point1[0])
# geom1 の一次関数に座標を当てはめ、geom2 の端点の領域をチェック
check1 = (a * point3[0]) - point3[1] + b
check2 = (a * point4[0]) - point4[1] + b
# 結果どうしの積がマイナス値なら True を戻す
if (check1 * check2) < 0:
return True
else:
return False
# main
# Lineの端点となる point を定義
p0 = geometry.Point(-2, -1)
p1 = geometry.Point(2, 3)
p2 = geometry.Point(-2, 1)
p3 = geometry.Point(3, 0)
p4 = geometry.Point(-1, -2)
p5 = geometry.Point(3, -1)
# Lineを定義
s1 = geometry.Line(p0, p1)
s2 = geometry.Line(p2, p3)
s3 = geometry.Line(p4, p5)
# グラフ描画
segments = [s1, s2, s3]
plt.figure(figsize=(5, 5), dpi=96)
for i, s in enumerate(segments):
plt_x = [s.p1.x, s.p2.x]
plt_y = [s.p1.y, s.p2.y]
# 交差チェック
intersects_check = my_intersects(s1, s)
if intersects_check:
plt.plot(plt_x, plt_y, color="red", linewidth=3)
else:
plt.plot(plt_x, plt_y)
xRange = yRange = (-4, 4)
plt.xlim(xRange)
plt.ylim(yRange)
plt.xticks(range(xRange[0], xRange[1]+1))
plt.yticks(range(yRange[0], yRange[1]+1))
plt.grid(color='blue', alpha=0.3)
plt.show()
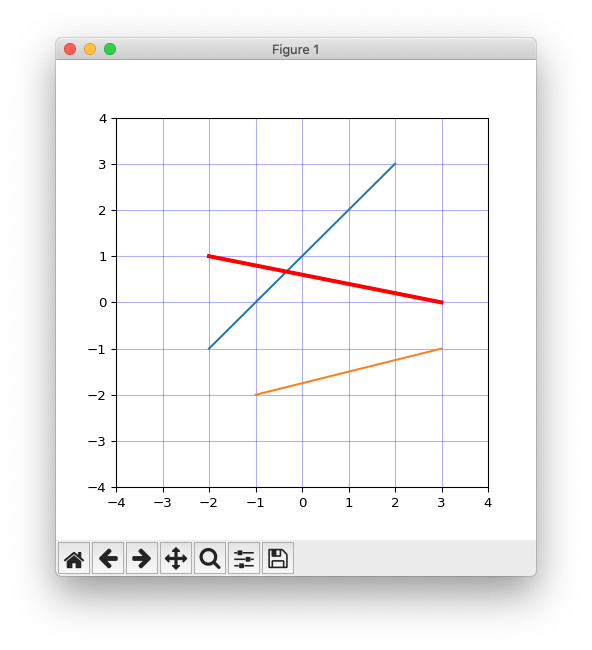
実行するとこんな感じのプロットを表示。
青線に交差する線は若干太くしています。
交差を判定する別の方法
今回は一次関数を用いて線の交差を判定してみましたが、方法はこれだけでなく、ベクトルの外積を使って交差を求める方法もあります。ですが、私がベクトルの外積を理解してないので今回はここまで。
また別の機会があれば検証してみたいと思います。