背景
カルマンフィルタについて勉強する機会があったので、まとめたいと考えました。
カルマンフィルタには線形モデルと非線形モデルに大きく分けられます。
今回は線形モデルをC++で実装したいと思います。
制御工学において、カルマンフィルタは基礎的な手法であるのにもかかわらず、
いざ取り掛かってみると、概要は理解できたものの、自信で使いこなすのには苦労します。(私は苦労しました。凡人なので。)
もし勉強している人がいるのであれば、
こちらでアルゴリズムを学び、実装できるきっかけになると私は嬉しいです。
また線形カルマンのC++のコードはpythonやRに比べて非常に少なく、
この点においても苦労した要因かなと思います。
あとmarkdown法で記述したかったのですが、時間の都合上できませんでした。
実装環境
window 10 64bit
visual studio 2017
言語 C++
行列計算ライブラリ Eigen
線形カルマンフィルタのモデル
モデルは様々は形式を作ることができますが、
今回は変位、速度、加速度の三要素を推定したいと思います。
提案モデル
いきなり言っていることが分からなくても、大丈夫です。
雰囲気でつかみ取ってください。
今回は単純な運動モデルを扱います。
具体的には得られるのは観測値(ノイズまじりの変位情報)で、
それから変位と速度と加速度を推定します。
線形状態空間モデルである状態方程式(1)と観測方程式(2)の2つを立式します。
これは自分が取り組み課題に応じて設計します。
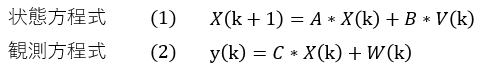
変数の説明
今回取り組む変数について、簡単に説明します。
状態ベクトル:推定する変数を変位、速度、加速度であるため、3つ準備します。
観測値:今回は得られる情報として、ノイズまじりの変位情報とします。
そのため、ベクトルではなくスカラーとして扱います。
係数行列A:変位と速度と加速度の関係式を行列に落とし込んだときの係数です。
オイラーの方程式が絡んできます。今回はΔT=1と仮定します。
係数行列B:状態ノイズと状態ベクトルの係数関係。
係数行列C:状態ノイズと観測値の係数関係。
状態ノイズ:運動状態に発生するノイズ。具体的には、空気抵抗や摩擦抵抗など。
観測ノイズ:観測するときに発生するノイズ。具体的には、センサーやカメラ自体のノイズ。
単位行列I.

アルゴリズム
簡単にいうと5つの式をループすることで、状態ベクトルを推定します。
はじめの2つが未来を予測する予測ステップで、
その他の3つが現在を推定するフィルタリングステップです。
k|k-1とはk-1ステップまでの値からkステップでの値を推定といったニュアンスです。
(厳密に表現すると文字数がかなり必要なので、割愛します。)
下の式からわかるように、事前状態方程式と事前誤差共分散行列を先に計算し予測し、
観測値によって状態推定値を補正するアルゴリズムとなってます。
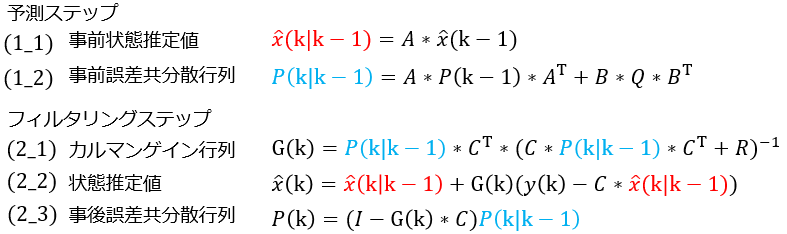
手計算をしてみよう、その前に事前準備
アルゴリズムを組み込む際に、コードの書き方が分からない。。。。という方は、
まずはk=1,k=2・・・を代入してみて、
1つ1つの式を紙に書き起こしてみると理解できるかもしれません。
その前に事前準備として、
初期値とノイズ値を決めておく必要があります。
計算方法はいくつかありますが、今回は以下のように仮定します。
できることであれば、初期値もノイズも予め推定する必要があります。
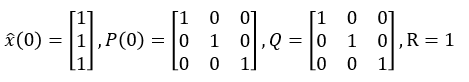
手計算をしてみよう
k=1を手計算してみました。
係数行列AでのΔT=1、観測値y(1)=2と仮定します。

計算のイメージはできそうでしょうか。
さらにk=2を自身で書いてみると、アルゴリズムをより理解できると思います。
C++の行列ライブラリ「Eigen」
見てわかる通り、行列を使う計算をたくさんします。
もちろんC++には配列という変数を設けることができますが、
少し使いずらく、中での行列計算がしんどいです。
そこで行列計算用外部ライブラリ[Eigen]を使用します。
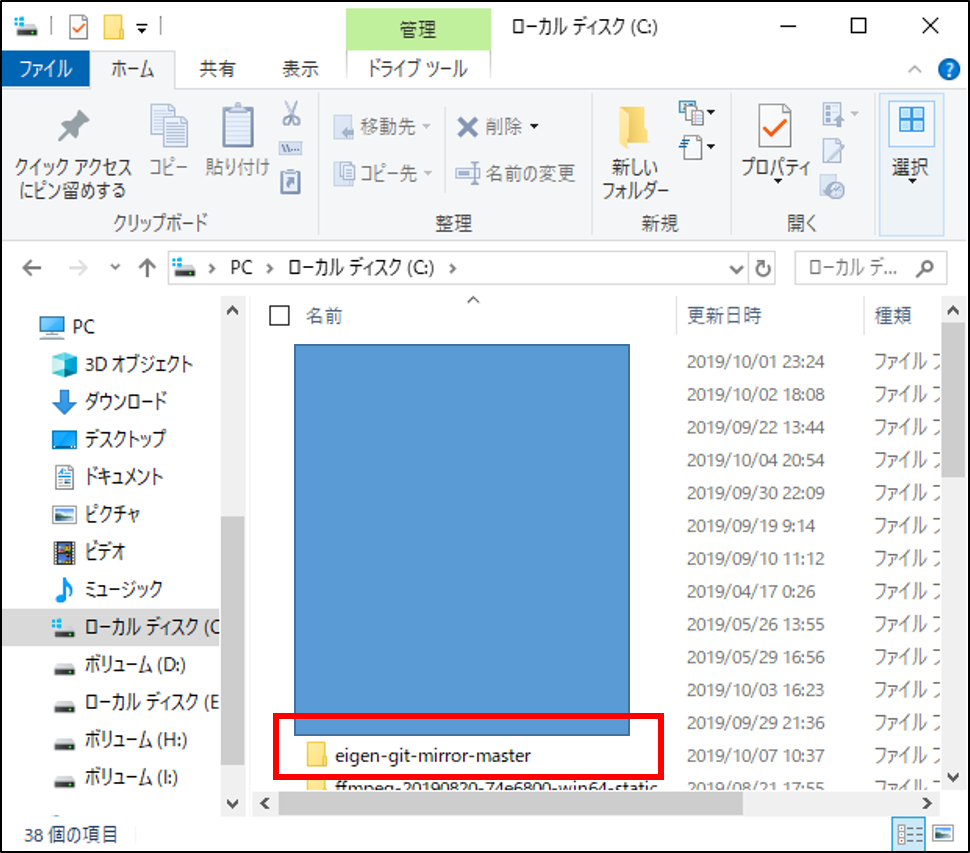
以下の公式リンクからダウンロード(クローンしなくても大丈夫です)し、Cドライブ直下にそのまま置いてください。
git clone https://github.com/eigenteam/eigen-git-mirror
ダウンロードしたら、次にvisual studioで新規のプロジェクトを作成します。
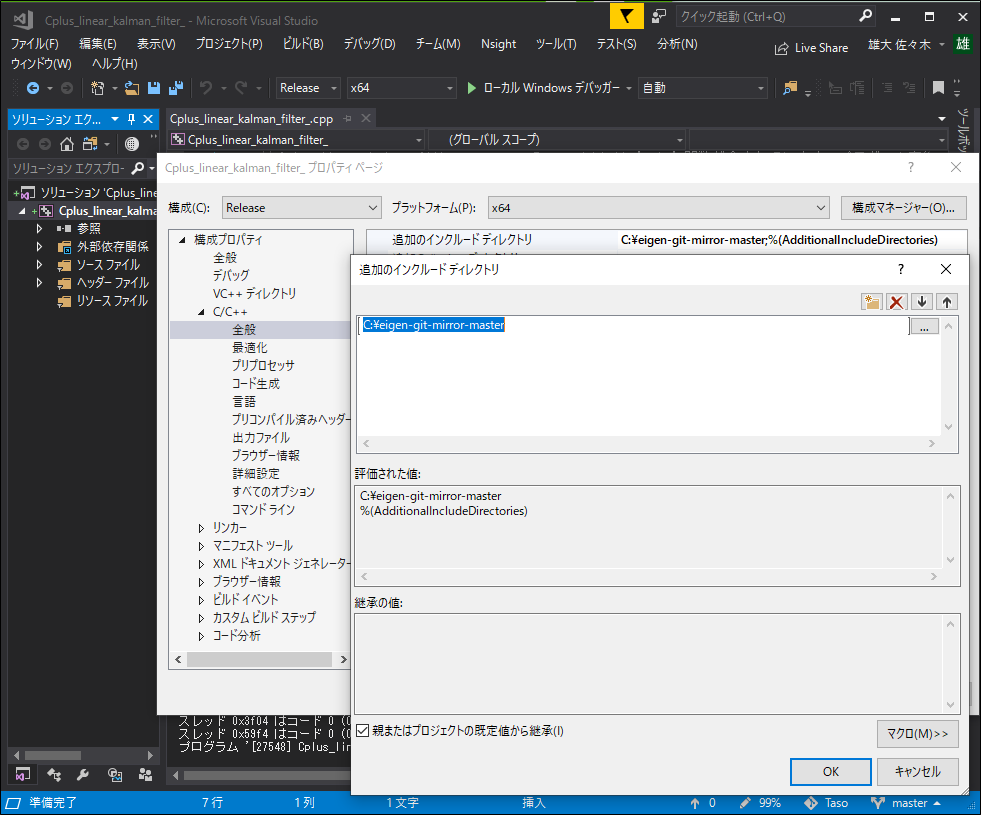
プロジェクトから右クリックでプロパティを開き、
C/C++ → 全般 → 追加のインクルードディレクトリ に進み、以下の入力します。
C:\eigen-git-mirror-master
カルマンフィルタのプログラム
ステップが上がるときに下記の関係式が成り立ち、
上書きされることを考慮してください。
参考コード k=1
とりあえずk=1のコードを記述します。
# include "pch.h"
# include <iostream>
# include <Eigen/Core>
using namespace Eigen;
int main()
{
Matrix3d A_(3, 3);//係数行列A
A_ << 1, 1, 0.5,
0, 1, 1,
0, 0, 1;
std::cout << "A_ = \n" << A_ << std::endl;
Matrix3d A_T(3, 3);//A_の転置行列
A_T = A_.transpose();
std::cout << "A_T = \n" << A_T << std::endl;
Matrix3d B_(3, 3);//係数行列B
B_ << 1, 0, 0,
0, 1, 0,
0, 0, 1;
std::cout << "B_ = \n" << B_ << std::endl;
Matrix3d B_T(3, 3); //B_の転置行列
B_T = B_.transpose();
std::cout << "B_T = \n" << B_T << std::endl;
Vector3d Ct_; //係数行列C 列ベクトル
Ct_ << 1, 0, 0;
std::cout << "Ct_ = \n" << Ct_ << std::endl;
MatrixXd C_ = Ct_.transpose();//係数行列C 行ベクトル
std::cout << "C_ = \n" << C_ << std::endl;
Matrix3d Q_(3, 3);//状態ノイズ
Q_ << 1, 0, 0,
0, 1, 0,
0, 0, 1;
std::cout << "Q_ = \n" << Q_ << std::endl;
double R_ = 1.0;//システムノイズ
Matrix3d I_(3, 3);//単位行列
I_ << 1, 0, 0,
0, 1, 0,
0, 0, 1;
Vector3d x_hat_k_k;//状態推定値に初期値を代入
x_hat_k_k << 1, 1, 1;
std::cout << "x_hat_k_k = \n" << x_hat_k_k << std::endl;
Matrix3d P_k_k(3, 3);//誤差共分散行列に初期値を代入
P_k_k << 1, 0, 0,
0, 1, 0,
0, 0, 1;
std::cout << "P_k_k = \n" << P_k_k << std::endl;
Vector3d x_hat_k_k1;//事前状態推定値
Matrix3d P_k_k1;//事前誤差共分散行列
Vector3d G_;//カルマンゲイン行列
double y[10] = { 2,4,6,8,10,12,14,16 };
/* k=1 */
// (1_1)
x_hat_k_k1 = A_ * x_hat_k_k;
std::cout << "x_hat_k_k1 = \n" << x_hat_k_k1 << std::endl;
//(1_2)
P_k_k1 = A_ * P_k_k * A_T + B_ * Q_ * B_T;
std::cout << "P_k_k1_ = \n" << P_k_k1 << std::endl;
//(2_1) 分母が1次元スカラーだったので、このように表現
G_ = P_k_k1 * Ct_ / ((C_ * P_k_k1 * Ct_)(0, 0) + R_);
std::cout << "G_ = \n" << G_ << std::endl;
//(2_2) 観測値 y[0] = 2
x_hat_k_k = x_hat_k_k1 + G_ * (y[0] - (C_ * x_hat_k_k1)(0, 0));
std::cout << "x_hat_k_k = \n" << x_hat_k_k << std::endl;
//(2_3)
P_k_k = (I_ - G_ * C_) * P_k_k1;
std::cout << "P_k_k = \n" << P_k_k << std::endl;
}
参考コード k=1,k=2
次にk=2までのコードを記述します。
観測値 y(2) = 4 とします。コートではy[1] = 4。
# include "pch.h"
# include <iostream>
# include <Eigen/Core>
using namespace Eigen;
int main()
{
Matrix3d A_(3, 3);//係数行列A
A_ << 1, 1, 0.5,
0, 1, 1,
0, 0, 1;
std::cout << "A_ = \n" << A_ << std::endl;
Matrix3d A_T(3, 3);//A_の転置行列
A_T = A_.transpose();
std::cout << "A_T = \n" << A_T << std::endl;
Matrix3d B_(3, 3);//係数行列B
B_ << 1, 0, 0,
0, 1, 0,
0, 0, 1;
std::cout << "B_ = \n" << B_ << std::endl;
Matrix3d B_T(3, 3); //B_の転置行列
B_T = B_.transpose();
std::cout << "B_T = \n" << B_T << std::endl;
Vector3d Ct_; //係数行列C 列ベクトル
Ct_ << 1, 0, 0;
std::cout << "Ct_ = \n" << Ct_ << std::endl;
MatrixXd C_ = Ct_.transpose();//係数行列C 行ベクトル
std::cout << "C_ = \n" << C_ << std::endl;
Matrix3d Q_(3, 3);//状態ノイズ
Q_ << 1, 0, 0,
0, 1, 0,
0, 0, 1;
std::cout << "Q_ = \n" << Q_ << std::endl;
double R_ = 1.0;//システムノイズ
Matrix3d I_(3, 3);//単位行列
I_ << 1, 0, 0,
0, 1, 0,
0, 0, 1;
Vector3d x_hat_k_k;//状態推定値に初期値を代入
x_hat_k_k << 1, 1, 1;
std::cout << "x_hat_k_k = \n" << x_hat_k_k << std::endl;
Matrix3d P_k_k(3, 3);//誤差共分散行列に初期値を代入
P_k_k << 1, 0, 0,
0, 1, 0,
0, 0, 1;
std::cout << "P_k_k = \n" << P_k_k << std::endl;
Vector3d x_hat_k_k1;//事前状態推定値
Matrix3d P_k_k1;//事前誤差共分散行列
Vector3d G_;//カルマンゲイン行列
double y[10] = { 2,4,6,8,10,12,14,16 };
/* k=1 */
// (1_1)
x_hat_k_k1 = A_ * x_hat_k_k;
std::cout << "x_hat_k_k1 = \n" << x_hat_k_k1 << std::endl;
//(1_2)
P_k_k1 = A_ * P_k_k * A_T + B_ * Q_ * B_T;
std::cout << "P_k_k1_ = \n" << P_k_k1 << std::endl;
//(2_1) 分母が1次元スカラーだったので、このように表現
G_ = P_k_k1 * Ct_ / ((C_ * P_k_k1 * Ct_)(0, 0) + R_);
std::cout << "G_ = \n" << G_ << std::endl;
//(2_2) 観測値 y[0] = 2
x_hat_k_k = x_hat_k_k1 + G_ * (y[0] - (C_ * x_hat_k_k1)(0, 0));
std::cout << "x_hat_k_k = \n" << x_hat_k_k << std::endl;
//(2_3)
P_k_k = (I_ - G_ * C_) * P_k_k1;
std::cout << "P_k_k = \n" << P_k_k << std::endl;
/* k=2 */
// (1_1)
x_hat_k_k1 = A_ * x_hat_k_k;
std::cout << "x_hat_k_k1 = \n" << x_hat_k_k1 << std::endl;
//(1_2)
P_k_k1 = A_ * P_k_k * A_T + B_ * Q_ * B_T;
std::cout << "P_k_k1_ = \n" << P_k_k1 << std::endl;
//(2_1) 分母が1次元スカラーだったので、このように表現
G_ = P_k_k1 * Ct_ / ((C_ * P_k_k1 * Ct_)(0, 0) + R_);
std::cout << "G_ = \n" << G_ << std::endl;
//(2_2) 観測値 y[0] = 2
x_hat_k_k = x_hat_k_k1 + G_ * (y[1] - (C_ * x_hat_k_k1)(0, 0));
std::cout << "x_hat_k_k = \n" << x_hat_k_k << std::endl;
//(2_3)
P_k_k = (I_ - G_ * C_) * P_k_k1;
std::cout << "P_k_k = \n" << P_k_k << std::endl;
}
参考コード k=1からk=10まで
次にk=10までのカルマンフィルタをループさせるコードを記述します。
# include "pch.h"
# include <iostream>
# include <Eigen/Core>
using namespace Eigen;
int main()
{
Matrix3d A_(3, 3);//係数行列A
A_ << 1, 1, 0.5,
0, 1, 1,
0, 0, 1;
std::cout << "A_ = \n" << A_ << std::endl;
Matrix3d A_T(3, 3);//A_の転置行列
A_T = A_.transpose();
std::cout << "A_T = \n" << A_T << std::endl;
Matrix3d B_(3, 3);//係数行列B
B_ << 1, 0, 0,
0, 1, 0,
0, 0, 1;
std::cout << "B_ = \n" << B_ << std::endl;
Matrix3d B_T(3, 3); //B_の転置行列
B_T = B_.transpose();
std::cout << "B_T = \n" << B_T << std::endl;
Vector3d Ct_; //係数行列C 列ベクトル
Ct_ << 1, 0, 0;
std::cout << "Ct_ = \n" << Ct_ << std::endl;
MatrixXd C_ = Ct_.transpose();//係数行列C 行ベクトル
std::cout << "C_ = \n" << C_ << std::endl;
Matrix3d Q_(3, 3);//状態ノイズ
Q_ << 1, 0, 0,
0, 1, 0,
0, 0, 1;
std::cout << "Q_ = \n" << Q_ << std::endl;
double R_ = 1.0;//システムノイズ
Matrix3d I_(3, 3);//単位行列
I_ << 1, 0, 0,
0, 1, 0,
0, 0, 1;
Vector3d x_hat_k_k;//状態推定値に初期値を代入
x_hat_k_k << 1, 1, 1;
std::cout << "x_hat_k_k = \n" << x_hat_k_k << std::endl;
Matrix3d P_k_k(3, 3);//誤差共分散行列に初期値を代入
P_k_k << 1, 0, 0,
0, 1, 0,
0, 0, 1;
std::cout << "P_k_k = \n" << P_k_k << std::endl;
Vector3d x_hat_k_k1;//事前状態推定値
Matrix3d P_k_k1;//事前誤差共分散行列
Vector3d G_;//カルマンゲイン行列
//観測値を以下のように得られたと仮定する
double y[10] = { 2,4,6,8,10,12,14,16,18,20 };
// k=0-9までの合計10
for (int i = 0; i < 10; i++) {
// (1_1)
x_hat_k_k1 = A_ * x_hat_k_k;
//(1_2)
P_k_k1 = A_ * P_k_k * A_T + B_ * Q_ * B_T;
//(2_1) 分母が1次元スカラーだったので、このように表現
G_ = P_k_k1 * Ct_ / ((C_ * P_k_k1 * Ct_)(0, 0) + R_);
//(2_2) 観測値 y[0] = 2
x_hat_k_k = x_hat_k_k1 + G_ * (y[i] - (C_ * x_hat_k_k1)(0, 0));
std::cout <<"x_hat_k_k[" <<i<<"] = \n" << x_hat_k_k << std::endl;
//(2_3)
P_k_k = (I_ - G_ * C_) * P_k_k1;
}
}
Github
今回のコードをアップさせていただきました。
git clone https://github.com/yusa0827/191007_Cplus2_linear_Kalman_FIlter_train
総括
線形カルマンフィルタの概要よりかは、解き方や扱い方についてまとめました。
全く分からないよぉというかたのお助けができれば、非常にうれしいです。
次は、初期値とノイズの推定法についてまとめれたらいいのかな、と思います。
最後に、ルドルフ・カルマンさんと[カルマンフィルタの基礎]の著者である足立修一先生に感謝の意をお伝えします。
改めてありがとうございました。
追記(2020/2/22) カルマンフィルタをクラス化
上記の処理だと、個人的に見栄えが悪いので、
カルマンフィルタ部分をヘッダーファイルにまとめました。
まとめることで、他の処理をするときに見やすくなります。
次に余裕があったら初期値推定も記述したいです。
フォルダ構想
ヘッダーファイル内で新規ファイルを作成し、ファイル名をclass_KalmanFilter.hとする。
また、メインファイルにはclass_KalmanFilter.hをインクルードします。
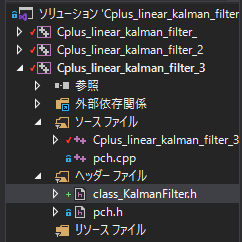
サンプルコード
# include "pch.h"
# include "class_KalmanFilter.h"
int main()
{
KALMAN_FILTER KF;//カルマンフィルタのオブジェクト作成
KF.init_menber();//カルマンフィルタのメンバー変数を初期化
double y[10] = { 2,4,6,8,10,12,14,16,18,20 };//k番目の観測値群
//k(=1,2,,,10)ステップまでのフィルタリング
for (int k = 0; k < 10; k++) {
KF.estimation_x_value(y[k]);//k番目のフィルタリング処理
std::cout << "x_hat_k_k[" << k << "] = \n" << KF.x_hat_k_k << std::endl;
}
}
# pragma once
# include <iostream>
# include <Eigen/Core>
using namespace Eigen;
//カルマンフィルタのクラス
class KALMAN_FILTER {
public:
Matrix3d A_;//係数行列A
Matrix3d A_T;//A_の転置行列
Matrix3d B_;//係数行列B
Matrix3d B_T; //B_の転置行列
Vector3d Ct_; //係数行列C 列ベクトル
MatrixXd C_;//係数行列C 行ベクトル
Matrix3d Q_;//状態ノイズ
double R_ = 1.0;;//システムノイズ
Matrix3d I_;;//単位行列
Vector3d x_hat_k_k;//状態推定値に初期値を代入
Matrix3d P_k_k;//誤差共分散行列に初期値を代入
Vector3d x_hat_k_k1;//事前状態推定値
Matrix3d P_k_k1;//事前誤差共分散行列
Vector3d G_;//カルマンゲイン行列
void init_menber();//メンバー変数の初期化
void estimation_X_value(double y);//観測値y
};
void KALMAN_FILTER::estimation_X_value(double y) {
// (1_1)
x_hat_k_k1 = A_ * x_hat_k_k;
//(1_2)
P_k_k1 = A_ * P_k_k * A_T + B_ * Q_ * B_T;
//(2_1) 分母が1次元スカラーだったので、このように表現
G_ = P_k_k1 * Ct_ / ((C_ * P_k_k1 * Ct_)(0, 0) + R_);
//(2_2) 観測値 y[0] = 2
x_hat_k_k = x_hat_k_k1 + G_ * (y - (C_ * x_hat_k_k1)(0, 0));
//(2_3)
P_k_k = (I_ - G_ * C_) * P_k_k1;
};
void KALMAN_FILTER::init_menber() {
A_ << 1, 1, 0.5,//係数行列A
0, 1, 1,
0, 0, 1;
A_T = A_.transpose();//A_の転置行列
B_ << 1, 0, 0,//係数行列B
0, 1, 0,
0, 0, 1;
B_T = B_.transpose();//B_の転置行列
Ct_ << 1, 0, 0;//係数行列C 列ベクトル
C_ = Ct_.transpose();//係数行列C 行ベクトル
Q_ << 1, 0, 0,//状態ノイズ
0, 1, 0,
0, 0, 1;
//R_ = 1.0;//システムノイズ
I_ << 1, 0, 0,//単位行列
0, 1, 0,
0, 0, 1;
x_hat_k_k << 1, 1, 1;//状態推定値に初期値を代入
P_k_k << 1, 0, 0, //誤差共分散行列に初期値を代入
0, 1, 0,
0, 0, 1;
};
参考文献
'論文' An Introduction to the Kalman Filter
'本' [カルマンフィルタの基礎] (https://www.amazon.co.jp/%E3%82%AB%E3%83%AB%E3%83%9E%E3%83%B3%E3%83%95%E3%82%A3%E3%83%AB%E3%82%BF%E3%81%AE%E5%9F%BA%E7%A4%8E-%E8%B6%B3%E7%AB%8B%E4%BF%AE%E4%B8%80/dp/4501328908)
'本' 応用カルマンフィルタ
C++行列計算ライブラリEigen入門