確率密度関数とは
累積分布関数の前に確率密度関数について説明していきます
確率密度関数とは、ある確率変数に対して確率密度という概念を対応づける関数のことです
2 つのサイコロを投げた時の和はいくつかという事象を例に挙げます
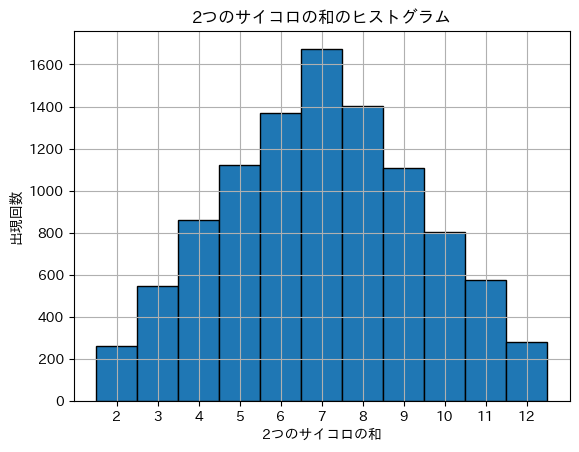
以上の図は先ほどの事象をは 10000 回試行した結果です
これを確率密度関数で表現してみます
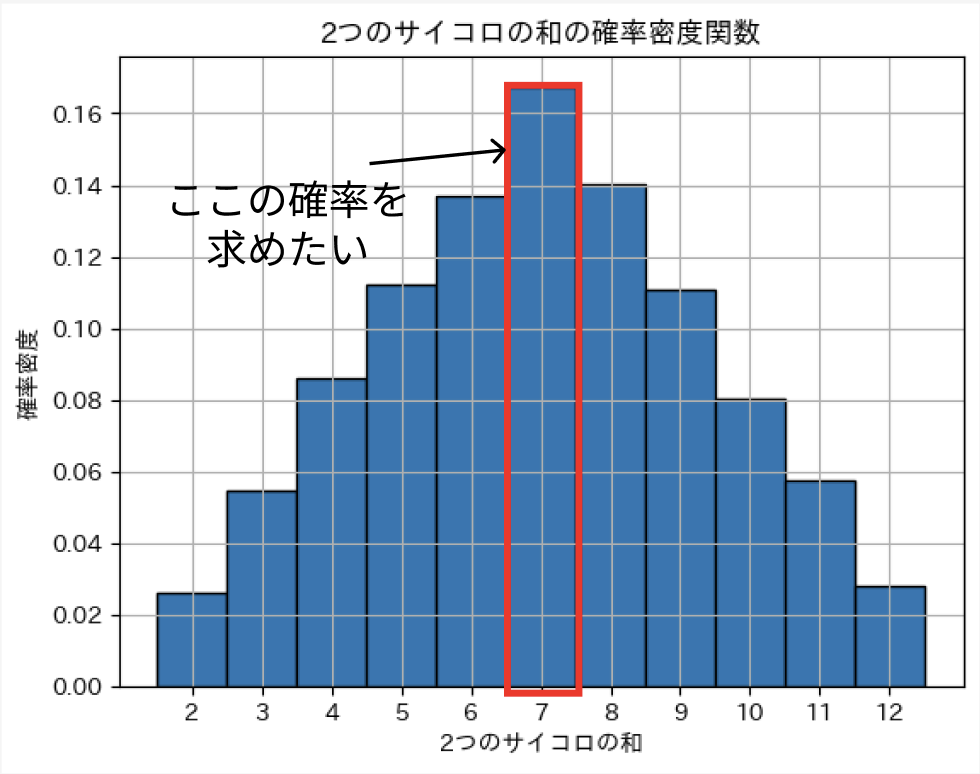
以上の図より 2 つのサイコロの和が 7 となる時の確率は大体 0.17 * 100 = 17%であるとわかります
理想状態で例に挙げた事象を検証すると 6/ 36 = 0.166.... なので大体あってそうですね
このように確率密度関数は確率変数一つを入力として渡すことで求めたい確率を求めることができます
累積分布関数とは
累積分布関数とは、確率変数がある値以下をとる時の確率を示す関数です
確率密度関数との違い
累積分布関数は確率密度関数とは異なり、複数の確率変数の和の確率を求めます
確率密度関数と累積分布関数それぞれに 7 を入力するとします
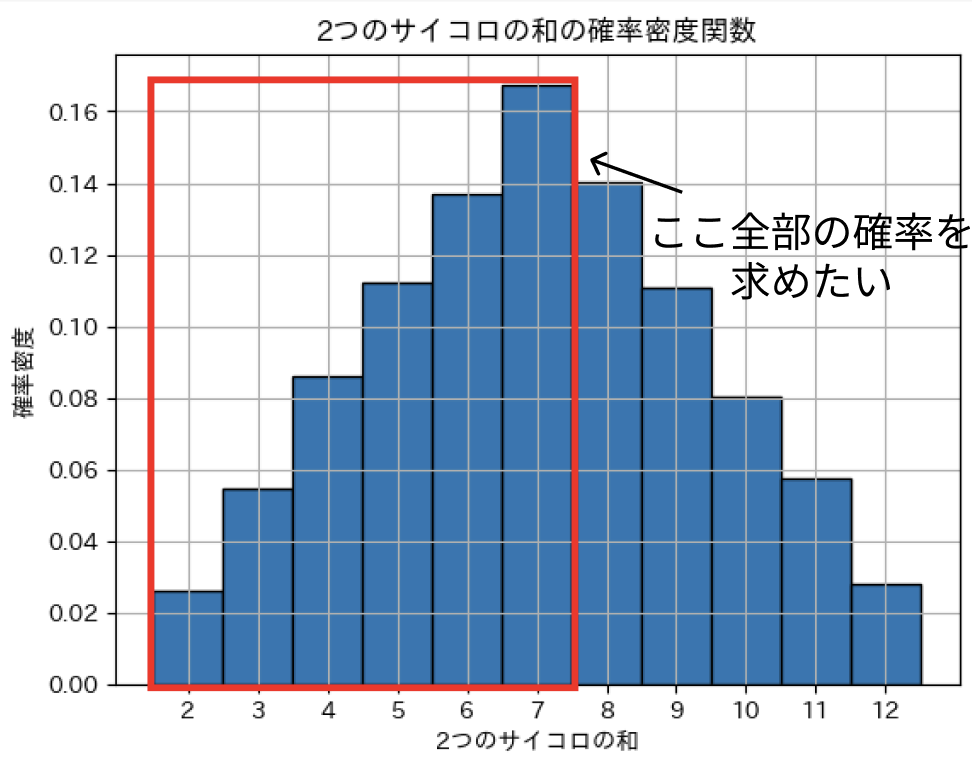
このとき、先ほどの図の説明すると確率密度関数では、7 が出る時のみの確率を求めるのに対し、累積分布関数では 7 よりも小さい確率変数の値の全ての確率を足した確率を求めます
このように累積分布関数は確率変数がある値以下をとる時の確率の総和を導出することができます
参考記事