はじめに
最近のWebGLデモはどれもクオリティ高いですね。いつも吐きそうになりながら、みさせていただいてます。
今回、初投稿になりますが、布(クロス)シミュレーションについて取り上げてみようと思います。
最近では、エンジンが吸収してくれたリしているおかげで、内部的な仕組みを理解していなくても、簡単に高品質な布シミュレーションが扱えてしまうのですが、それもなんか悔しいなぁということで、WebGLで一から勉強して実装してみました。
結果、それなりの見た目にまで仕上げることができましたので、得られた知見などまとめてみようと思います。
完成品
下記のURLから完成品のデモページに飛びます。
PC環境でのChromeまたはFirefoxで動作確認済です(スマホからは動かないかもしれません)
ソースの全体確認は、お手数ですがブラウザのデバッガからどうぞ。
● CPUベースの実装
http://yrlab.zatunen.com/webgl/cloth/cloth.html

● GPUベースの実装
http://yrlab.zatunen.com/webgl/gpucloth/gpucloth.html
CPU Based Cloth Simulation
まずは、CPUベースの実装で、布シミュレーションの基本的な仕組みについて追っていきます。
本実装では、最もポピュラーな質点バネモデル(Mass-spring model)を使用します。
簡単に言うと、布の形状にあわせて格子状に配置した質点をバネで繋いで、質点に外から与えられた力と質点同士が相互に及ぼし合うバネの力を計算することで、布の運動挙動を近似するというアプローチです。
まずは大枠から
布シミュレーションの外殻をざっくり表すとこんな構造になっています。
onload = function()
{
/* …… */
main_loop();
function main_loop()
{
/* …… */
// 布の初期化(初回またはリセット時のみ)
if(reset)
{
init();
reset = false;
}
// 布の更新
update();
// 布の描画
render();
requestAnimationFrame(main_loop);
}
}
実際、更新の箇所はもう少し複雑です。
可変フレームレートに対応させているのですが、フレーム間の差分時間をそのまま更新関数に渡してしまうと、処理落ちなどが発生した際に、布に想定外の大きな力が加わってしまい、計算が破綻してしまいます。
そこで、更新関数に渡すタイムステップは固定してしまい、フレーム間の差分時間が大きい場合は、複数回更新関数を呼んでやることで一定の計算精度を保っています。
タイムステップが小さいほど計算精度が高くなりますが、1フレームに何回も更新関数が呼ばれることになるので、当然処理とのトレードオフになります。
// 更新
const ms_step = 16; // シミュレーションのタイムステップ(固定)
let ms_delta = timer._ms_delta + ms_surplus; // フレームの差分時間
ms_delta = Math.min(ms_delta, 100); // リミッター
while(ms_delta >= ms_step)
{
// 大きなタイムステップでシミュレーションを実行すると精度の問題で破綻が生じるため、
// フレームの差分時間を固定のシミュレーションタイムステップで分割し、複数回処理する。
// 余剰時間は次のフレームに持ち越す。
update(ms_step / 1000.0, ms_acc / 1000.0);
ms_acc += ms_step;
ms_delta -= ms_step;
}
ms_surplus = ms_delta;
初期化
布をグリッド分割するように質点を配置します。質点は、現在位置、前回位置、重み、を持ちます。
前回位置は後に説明するベルレ積分で使用します。また、重みはその質点が固定されているか否かを表します。デモでは布の上部を固定しているため、上部の辺に配置される質点の重みは0.0になります。その他の質点は1.0です。
// 質点
function ClothPoint()
{
this._pos = vec3.create(); // 現在位置
this._pre_pos = vec3.create(); // 前の位置
this._weight = 0.0; // 運動計算の重み(固定点は0.0、そうでなければ1.0)
}
次に、布にバネを仕込んでいきます。このバネのことを便宜上「制約(コンストレイント)」と呼びます。
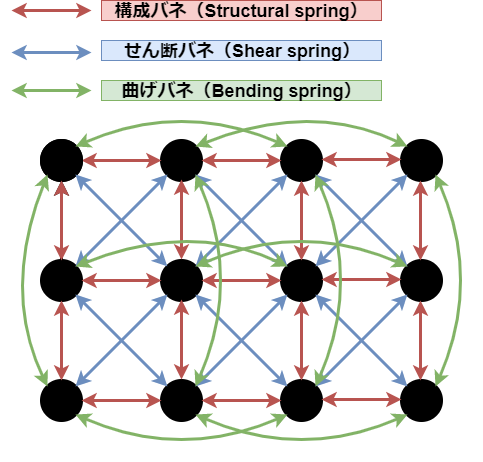
下の図は、質点が4*3の簡易的な布の構成イメージです
● 赤色のバネは「構成バネ(Structural spring)」と呼ばれ、布の形状を維持するための最も基本的なバネになります。
● 青色のバネは「せん断バネ(Shear spring)」と呼ばれ、布のせん断に対して働きます。
● 緑色のバネは「曲げバネ(Bending spring)」と呼ばれ、布が曲がろうとする力に対して抵抗する突っ張り棒のような働きをし、より自然な皺を表現できるようになります。
制約(バネ)は、接続された2つの質点、バネの自然長(質点間の基本となる距離)、バネの種類、を持ちます。
// 制約(バネ)
function ClothConstraint()
{
this._p1 = undefined; // 質点1
this._p2 = undefined; // 質点2
this._rest = 0.0; // バネの自然長
this._type = 0; // バネの種類(0..構成バネ, 1..せん断バネ, 2..曲げバネ)
}
この他に、制約を計算する際、バネの強度(バネ定数)、バネの伸びに対する抵抗と縮みに対する抵抗、をそれぞれ考慮することで、異なる性質の布を表現できます。
下記、オリジナルの文献に詳細が書かれています(Landerのモデルと呼ばれるもの)
● Devil in the Blue Faceted Dress: Real Time Cloth Animation
https://www.gamasutra.com/view/feature/131851/devil_in_the_blue_faceted_dress_.php
初期化のソース
function Cloth(scale, div)
{
this._scale = scale; // スケーリング(ベースのサイズは2*2)
this._div = div; // 質点分割数
// 質点の作成と初期化
this._points = [];
for(let y = 0; y < this._div + 1; y++)
{
for(let x = 0; x < this._div + 1; x++)
{
const point = new ClothPoint();
point._pos[0] = x / this._div * 2.0 - 1.0;
point._pos[1] = 1.0;
point._pos[2] = y / this._div * 2.0;
vec3.scale(point._pos, point._pos, this._scale);
vec3.copy(point._pre_pos, point._pos);
point._weight = (y === 0) ? 0.0 : 1.0; // 落ちないように一辺を固定する
this._points.push(point);
}
}
// 制約の作成と初期化
this._constraints = [];
for(let y = 0; y < this._div + 1; y++)
{
for(let x = 0; x < this._div + 1; x++)
{
// 構成バネ(Structural springs)
this._constraints.push(this.genConstraint(x, y, -1, 0, 0)); // 左
this._constraints.push(this.genConstraint(x, y, 0, -1, 0)); // 上
// せん断バネ(Shear springs)
this._constraints.push(this.genConstraint(x, y, -1, -1, 1)); // 左上
this._constraints.push(this.genConstraint(x, y, 1, -1, 1)); // 右上
// 曲げバネ(Bending springs)
this._constraints.push(this.genConstraint(x, y, -2, 0, 2)); // 1つ飛ばし左
this._constraints.push(this.genConstraint(x, y, 0, -2, 2)); // 1つ飛ばし上
}
}
// 描画用頂点情報
this._vertices = []; // 頂点座標
this._indeces = []; // 頂点インデクス
this.genVertices();
this.genIndeces();
}
// 制約生成
Cloth.prototype.genConstraint = function(x, y, offsetX, offsetY, type)
{
const targetX = x + offsetX;
const targetY = y + offsetY;
if(targetX >= 0 && targetX < this._div + 1 && targetY >= 0 && targetY < this._div + 1)
{
const constraint = new ClothConstraint();
constraint._p1 = this._points[y * (this._div + 1) + x];
constraint._p2 = this._points[targetY * (this._div + 1) + targetX];
constraint._rest = this._scale * 2.0 / this._div * Math.sqrt(offsetX * offsetX + offsetY * offsetY);
constraint._type = type;
return constraint;
}
return undefined; // 範囲外
}
// 頂点座標生成
Cloth.prototype.genVertices = function()
{
/* 省略 */
}
// 頂点インデクス生成
Cloth.prototype.genIndeces = function()
{
/* 省略 */
}
更新
大きく分けて、3つのフェーズに分かれています。
便宜的に「積分フェーズ」「制約充足フェーズ」「衝突判定フェーズ」と呼びます。
積分フェーズ
このフェーズでは、質点の現在速度による変位(移動量)と、重力、風力、抵抗などによる変位を足し合わせて、質点の新しい位置を算出します。
まずは、基本的な運動法則のおさらいから。
ある速度で移動している物体に対して力を加えた際、更新後の物体位置は下記の計算で求められます。
vec3 f; // 力
float m; // 質量
/* としたとき、加速度aは */
vec3 a = f / m;
vec3 p; // 位置
vec3 v; // 速度
vec3 a; // 加速度
vec3 delta; // 更新にかかった時間
/* とすると、新しい位置new_pは */
vec3 new_p = p + v * delta + 0.5 * a * delta * delta;
今回使用するベルレ法(ベルレ積分)では、現在位置と前回位置を記録し、その差分を速度として扱います。つまり速度を記録する必要がありません。
対して、速度と位置を毎フレーム記録し、速度を更新してから位置を計算する方法をオイラー法といいます。
例えば、あるパーティクルが壁に衝突したとき、ベルレ法では、計算後のパーティクル位置を壁の表面位置まで押し戻してやるだけです。速度は後から自動的に合わさります(反射を考慮する場合は、計算前位置を壁の内部に書き換えるなどする必要あり)
このシンプルさが、後に解説するGPGPUとも相性がよかったりします。
ベルレ積分!とか言われると身構えてしまいそうですが、全然難しくないです。知らず知らずのうちに使っていたということも多いかと思います。
制約充足フェーズ
質点を繋ぐ制約の計算をします。
ここでは、フックの法則をそのまま使用しています。
float f; // バネの力
float k; // バネ定数(バネの強度)
float rest; // バネの自然長
float d; // 現在のバネの長さ
/* とすると */
f = (d - rest) * k; // 伸びに抵抗し、縮もうとする力がプラス
フックの法則より算出された力を変位に変換し、制約に接続された2つの質点をお互いに移動させます。これを全ての制約に対して行います。
ここで厄介な問題が発生します。
質点には複数の制約が接続されているため、ある制約を解決して質点位置を移動させると、他の接続されている制約との位置関係がずれてしまうのです。
また、実際には制約は一度に解決されず、バネの力により徐々に逐次的に処理されるので、質点の分割数を上げれば上げるほど伝播が遅くなり反応が悪くなってしまいます。これは布が不自然に伸び縮みしてしまうという現象となって現れます。
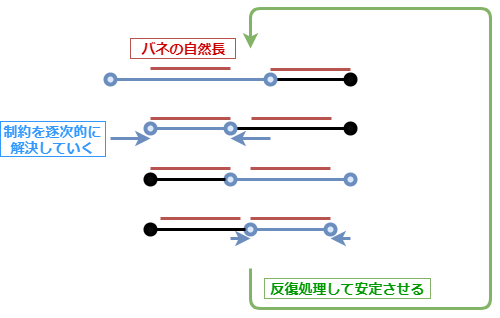
これに対して「Relaxation」という手法が考案されています。
何かというと、あっけにとられるほど単純で、制約計算全体を反復して行うというだけです。
反復回数が多いほど、挙動は安定し剛性のある布となりますが、処理とのトレードオフになります。
衝突判定フェーズ
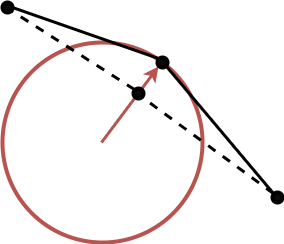
最も単純な球との衝突判定のみとっています。
これまでに算出された質点の位置が、球の内部にめり込んだ場合、球の表面まで押し出してやっているだけです。
ベルレ積分の性質で、位置を上書きすると、速度も自動的に更新されることになるので非常に楽です。
掘り下げると、もっと複雑なジオメトリや自由形状との衝突判定、自己衝突判定、摩擦、など、難しい話が飛び交う箇所でもあります。ここではそこまで深追いしていません。
更新のソース
Cloth.prototype.update = function(step, acc, relaxation, g, w, r, k, structural_shrink, structural_stretch, shear_shrink, shear_stretch, bending_shrink, bending_stretch, collision)
{
// 質点の質量は質点分割数にかかわらず1.0固定とします
// ただ、これだと質点分割数によって布のトータル質量が変わってしまうので、力に質量をかけて相殺しておきます
// 実質、この実装では質量が意味をなしていないのでmは不要ですが、見通しのため残しておきます
const m = 1.0; // 質点の質量
g *= m; // 重力
w *= m; // 風力
k *= m; // 制約バネの基本強度
// 積分フェーズ
{
// 重力と風力による変位(移動量)を計算しておく
const f = vec3.create();
f[1] -= g; // 重力
f[2] += w * (Math.sin(acc) * 0.5 + 0.5); // 風力(適当になびかせる)
vec3.scale(f, f, step * step * 0.5 / m); // 力を変位に変換しておく
// 抵抗は速度に対して働く
r = 1.0 - r * step;
for(const point of this._points)
{
// 変位
const dx = vec3.create();
vec3.sub(dx, point._pos, point._pre_pos); // 速度分
vec3.copy(point._pre_pos, point._pos); // 更新前の位置を記録しておく
vec3.add(dx, dx, f); // 力の変位を足しこむ
vec3.scale(dx, dx, r); // 抵抗
// 位置更新
vec3.scale(dx, dx, point._weight); // 固定点は動かさない
vec3.add(point._pos, point._pos, dx);
}
}
// 制約充足フェーズ
for(let ite = 0; ite < relaxation; ite++) // 反復処理して安定させる(Relaxationと呼ばれる手法)
{
for(const constraint of this._constraints)
{
if(constraint === undefined)
{
// 無効な制約
continue;
}
if(constraint._p1._weight + constraint._p2._weight === 0.0)
{
// 二つの質点がお互いに固定点であればスキップ(0除算防止)
continue;
}
// 伸び抵抗と縮み抵抗
let shrink = 0.0; // 伸び抵抗
let stretch = 0.0; // 縮み抵抗
if(constraint._type === 0)
{
// 構成バネ
shrink = structural_shrink;
stretch = structural_stretch;
}
else if(constraint._type === 1)
{
// せん断バネ
shrink = shear_shrink;
stretch = shear_stretch;
}
else if(constraint._type === 2)
{
// 曲げバネ
shrink = bending_shrink;
stretch = bending_stretch;
}
// バネの力(スカラー)
const d = vec3.distance(constraint._p2._pos, constraint._p1._pos); // 質点間の距離
let f = (d - constraint._rest) * k; // 力(フックの法則、伸びに抵抗し、縮もうとする力がプラス)
f >= 0 ? f *= shrink : f *= stretch; // 伸び抵抗と縮み抵抗に対して、それぞれ係数をかける
// 変位
const dx = vec3.create();
vec3.sub(dx, constraint._p2._pos, constraint._p1._pos); // 力(スカラー)を力(ベクトル)に変換
vec3.normalize(dx, dx); //
vec3.scale(dx, dx, f); //
vec3.scale(dx, dx, step * step * 0.5 / m); // 力を変位に変換
// 位置更新(二つの質点を互いに移動させる)
const dx_p1 = vec3.create();
vec3.scale(dx_p1, dx, constraint._p1._weight / (constraint._p1._weight + constraint._p2._weight));
vec3.add(constraint._p1._pos, constraint._p1._pos, dx_p1);
const dx_p2 = vec3.create();
vec3.scale(dx_p2, dx, constraint._p2._weight / (constraint._p1._weight + constraint._p2._weight));
vec3.sub(constraint._p2._pos, constraint._p2._pos, dx_p2);
}
}
// 衝突判定フェーズ
if(collision)
{
// 衝突判定用の球を適当に定義
const sphere_pos = vec3.fromValues(0.0, 0.0, 0.0); // 球の中心位置
const sphere_radius = 0.75; // 球の半径
for(const point of this._points)
{
// 球とのヒット
const v = vec3.create();
vec3.sub(v, point._pos, sphere_pos);
const d = vec3.length(v);
if(d < sphere_radius)
{
// ヒットしたので球の表面に押し出す
vec3.scale(v, v, sphere_radius / d);
vec3.add(point._pos, sphere_pos, v);
}
}
}
// 描画用頂点座標を更新
// Todo : 1フレームに1回呼べばいい
this.genVertices();
}
描画
本デモでは、描画をオレオレWebGLラッパーで行っているため、詳細説明は省きますが、
基本的には、質点を頂点として、ワイヤーフレームなりトライアングルなりを好きなように繋げてやるだけです。
※注意
本デモでは、毎フレーム頂点バッファを作り直すという残念なプログラムになっていますので、ここに関してはあまり参考にしない方がいいです。
詳しくないのですが、動的バッファ的なアプローチをとるのが正しいと思います。また、インターリーブ配列なども気にすると更によいと思います。
この辺りのVBO最適化については、@doxas 様、@emadurandal 様 が、とても詳しい記事を書かれており、とても参考になります。
● VBOを逐次更新しながら描画する
https://wgld.org/d/webgl/w081.html
● インターリーブ配列 VBO
https://wgld.org/d/webgl/w088.html
● GPU本来の性能を引き出すWebGL頂点データ作成法
https://qiita.com/emadurandal/items/0bb83b545670475f51a3
休憩
以上が、CPUベースでの実装になります。一つずつ噛み砕くと、そこまで難解な数式が出てくるわけでもなく、思ったよりはスムーズにいけたなという感じです。ただ、布らしくみせるパラメーター調整は正解が見え辛くしんどいですね。
では、これまでの実装をGPUベースに移植していきたいと思います。
と、その前に。
本デモは、WebGL1.0と一部の拡張機能(浮動小数点テクスチャ、頂点テクスチャフェッチ)を使用して、昔ながらのテクスチャベースのGPGPUで実装していきます。
詳細は、@doxas 様 の記事にお任せしてしまいます。
細かな実装は異なりますが、基本的な考え方は同じです。
● GPGPU でパーティクルを大量に描く
https://wgld.org/d/webgl/w083.html
最近知ったのですが、WebGL2.0にはTransform Feedbackという機能があり、頂点シェーダーで更新したVBOをラスタライザに流さず、再取得できるそうです。
おそらく、テクスチャベースよりも応用が効きますし、もっと整理されたコーディングができそうですね。
(WebGPUとか次世代がくれば、また事情が変わってくるのかな?)
それはさておき、基本的な考え方は大きく変わらないはずです。
では、GPUベースの実装に入っていきます。
GPU Based Cloth Simulation
布が高解像度になり、それに応じたパラメーター調整を行っています。また、トライアングルポリゴン&それっぽいライティングでの描画になっています。それ以外は、基本的にCPUベースと同じ挙動です。
ソースも可能な限り一対一で対応するように書きました(とはいってもかなり見辛くなっているかも)
GPUベースでの実装のポイントを抜き出してみていきます。
初期化
質点の状態を保存するために、3枚のフレームバッファを使用します。
● 計算結果を書き込むフレームバッファ
● 現在の情報が格納されたフレームバッファ
● 前回の情報が格納されたフレームバッファ
フレームバッファは、浮動小数点数フォーマットを使用します。
● RGB .. 位置
● A .. 重み
最初に、初期位置を現在位置と前回位置のフレームバッファに書き込んでおきます。
次に、描画用のジオメトリ(表面と裏面の2つ)を作成します。
座標情報はフレームバッファから取得するので、VBOにはそのためのUVを入れておきます。
はまりどころ
例えば、解像度2*2のフレームバッファにUV値(0.0~1.0)の矩形を書き込んだとします。
このとき、頂点シェーダーからラスタライザを通り、ピクセルシェーダーに渡されるUV値は、
(0.25, 0.25) (0.75, 0.25)
(0.25, 0.75) (0.75, 0.75)
のような形になります。
もし、ピクセルシェーダーで受け取ったUV値を布の位置情報としてそのまま書き込む場合、大きさ1.0になって欲しいところが、実際には、大きさ0.5であったりするわけです。
このことを考慮しておかないと、後の制約の距離計算に誤差が生じて、布の挙動が不安定になってしまう恐れがあります(布の解像度が十分に大きいと気付きづらいので見落としやすい)
これは、描画用ジオメトリのVBOに設定するUV値にも同様のことが言え、頂点シェーダーでテクスチャをフェッチする場合はUV値を半テクセル分ずらしておく必要があります。
// 描画用のジオメトリを作成
// VBOには、フレームバッファを頂点シェーダーでフェッチするためのUVを入れておく
const vertices = [];
for(let y = 0; y < (div + 1); y++)
{
for(let x = 0; x < (div + 1); x++)
{
// 正しくテクスチャサンプリングするために半テクセルずらしておく
// (通常は頂点シェーダーからピクセルシェーダーへ値が渡る際に処理されるので気にしないが、頂点シェーダーでテクスチャサンプリングする場合は気にする必要がある)
vertices.push((x + 0.5) / (div + 1));
vertices.push((y + 0.5) / (div + 1));
vertices.push(0.0);
}
}
初期化のシェーダー
// -------------------------------------------------------------------------------------------
// 初期化
// 頂点シェーダー
// vs_gpu_cloth_init
attribute vec3 a_position;
attribute vec2 a_uv0;
uniform mat4 u_wvp; /* WVP行列 */
uniform float u_div; /* 質点分割数 */
varying vec2 v_uv0;
void main()
{
/* フラグメントシェーダーでUVを0.0-1.0の範囲で受け取るための補正計算 */
v_uv0 = a_uv0 * (u_div + 1.0) / u_div - 0.5 / u_div;
gl_Position = u_wvp * vec4(a_position, 1.0);
}
// -------------------------------------------------------------------------------------------
// 初期化
// フラグメントシェーダー
// fs_gpu_cloth_init
/*precision mediump float;*/
precision highp float;
uniform float u_scale; /* 布の大きさに対するスケーリング */
uniform float u_div; /* 質点分割数 */
varying vec2 v_uv0;
void main()
{
/* RGB..座標 A..重み */
vec4 pos = vec4(
v_uv0.x * 2.0 - 1.0,
1.0,
v_uv0.y * 2.0,
v_uv0.y < 0.5 / (u_div + 1.0) ? 0.0 : 1.0
);
pos.xyz *= u_scale;
gl_FragColor = pos;
}
更新
CPUベースでは、一つの制約を解決する際に、接続されている2つの質点を同時に移動させ、これを制約毎に逐次的に処理しましたが、GPUベースでは、アプローチが異なります。
● 一度に移動させられる質点は1つのみ
質点(ピクセル)毎にシェーダーが走るので当然ですね。
● 一回の描画パスでは、1つの質点に対して1つの制約のみ処理できる。
並列処理なので、質点情報の書き換えと読み込みが競合しないようにする必要があるためです。
つまり、1つの質点には12本の制約が接続されているので、描画もここだけで、最低12パス必要ということになります。
しかも、これにRelaxationが入るので、実際には12 * n パス必要になります。
折角のGPGPUなのに、うまく並列化できない感じが、なんか勿体ないですね。
具体的には、下記のような実装になります。
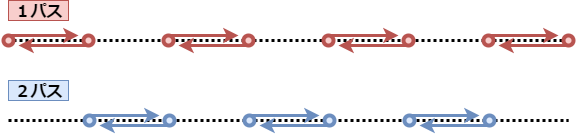
左右方向への構成バネの制約を考える場合、2パスに分けてこれを処理します。
例えば、1パス目は、計算中の質点が偶数番の場合は右への制約を考え、奇数番の場合は左への制約を考えます。
2パス目は、偶数番が左、奇数番が右、と反転させます。これで、干渉し合わない制約セットに分けることができました。
曲げバネの場合は、
右・右・左・左・右・右・左・左……
のような制約セットになります。
更新のシェーダー
// -------------------------------------------------------------------------------------------
// 更新
// 頂点シェーダー
// vs_gpu_cloth_update
attribute vec3 a_position;
attribute vec2 a_uv0;
uniform mat4 u_wvp; /* WVP行列 */
varying vec2 v_uv0;
void main()
{
v_uv0 = a_uv0;
gl_Position = u_wvp * vec4(a_position, 1.0);
}
// -------------------------------------------------------------------------------------------
// 更新(積分)
// フラグメントシェーダー
// fs_gpu_cloth_update_integration
/*precision mediump float;*/
precision highp float;
uniform sampler2D u_texture0;
uniform sampler2D u_texture1;
uniform vec3 u_dx; /* 重力と風力による変位 */
uniform float u_r; /* 抵抗 */
varying vec2 v_uv0;
void main()
{
vec2 uv = v_uv0;
uv.y = 1.0 - uv.y;
vec4 pos_now = texture2D(u_texture0, uv);
vec4 pos_old = texture2D(u_texture1, uv);
vec3 dx = pos_now.xyz - pos_old.xyz;
dx += u_dx;
dx *= u_r;
dx *= pos_now.w;
gl_FragColor = vec4(pos_now.xyz + dx, pos_now.w);
}
// -------------------------------------------------------------------------------------------
// 更新(制約充足)
// フラグメントシェーダー
// fs_gpu_cloth_update_constraint
/*precision mediump float;*/
precision highp float;
uniform sampler2D u_texture0;
uniform float u_div; /* 質点分割数 */
uniform vec2 u_neightbor_offset; /* もう1つの質点へのUVオフセット */
uniform float u_neightbor_coefficient; /* 干渉し合わない制約セットをつくるために使用する係数 */
uniform float u_rest; /* バネの自然長 */
uniform float u_k; /* バネ定数 */
uniform float u_shrink; /* バネの伸び抵抗 */
uniform float u_stretch; /* バネの縮み抵抗 */
uniform float u_f2dx; /* 力から変位に変換する計算 */
varying vec2 v_uv0;
vec2 neightbor(vec2 uv)
{
/* 制約の接続方向を一定周期に反転させることで、干渉しあわない制約セットをつくる */
vec2 of = u_neightbor_offset;
vec2 stp = step(0.5, mod(uv * (u_div + 1.0) / u_neightbor_coefficient, 1.0));
of = of * stp - of * (1.0 - stp);
return uv + of;
}
void main()
{
vec2 uv = v_uv0;
uv.y = 1.0 - uv.y;
vec4 pos1 = texture2D(u_texture0, uv);
if (pos1.w == 0.0) {
gl_FragColor = pos1;
return;
}
vec2 uv_neightbor = neightbor(uv);
if (
uv_neightbor.x < 0.0 ||
uv_neightbor.x > 1.0 ||
uv_neightbor.y < 0.0 ||
uv_neightbor.y > 1.0
) {
gl_FragColor = pos1;
return;
}
vec4 pos2 = texture2D(u_texture0, uv_neightbor);
float d = length(pos2.xyz - pos1.xyz);
float f = (d - u_rest) * u_k;
float stp = step(0.0, f);
f *= u_shrink * stp + u_stretch * (1.0 - stp);
vec3 dx = normalize(pos2.xyz - pos1.xyz) * f * u_f2dx;
pos1.xyz += dx * pos1.w / (pos1.w + pos2.w);
gl_FragColor = pos1;
}
// -------------------------------------------------------------------------------------------
// 更新(衝突判定)
// フラグメントシェーダー
// fs_gpu_cloth_update_collision
/*precision mediump float;*/
precision highp float;
uniform sampler2D u_texture0;
uniform vec3 u_sphere_pos; /* 球の中心位置 */
uniform float u_sphere_radius; /* 球の半径 */
varying vec2 v_uv0;
void main()
{
vec2 uv = v_uv0;
uv.y = 1.0 - uv.y;
vec4 pos = texture2D(u_texture0, uv);
vec3 v = pos.xyz - u_sphere_pos;
float d = length(v);
float stp = step(0.0, d - u_sphere_radius);
pos.xyz = pos.xyz * stp + (u_sphere_pos + v * u_sphere_radius / d) * (1.0 - stp);
gl_FragColor = pos;
}
描画
フレームバッファを頂点シェーダーでフェッチして、質点の座標を取得します。
このとき、隣り合う質点へのベクトルの外積から、法線を求めてライティングに使用しています。
面法線を頂点に設定することになるので、ライティングにアーティファクト(ガビガビ)が表れてしまっています。
本当は面法線から頂点法線を求めた方が綺麗なのかと思いますが、簡単な実装方法が思い浮かびませんでした……。
描画のシェーダー
// ------------------------------------------------------------------------------------------------
// 描画
// 頂点シェーダー
// vs_gpu_cloth_render
attribute vec3 a_position;
uniform sampler2D u_texture0;
uniform mat4 u_wvp; /* WVP行列 */
uniform mat4 u_matrix_for_normal; /* 法線用の行列 */
uniform float u_neightbor_offset; /* 隣の質点へのUVオフセット */
uniform float u_face; /* 表面(1.0)か裏面(-1.0)か */
varying vec3 v_wpos;
varying vec3 v_normal;
void main()
{
/* ライティングしたいので、面法線を計算しておく */
vec2 uv = a_position.xy;
uv.y = 1.0 - uv.y;
float offset_x = uv.x + u_neightbor_offset < 1.0 ? u_neightbor_offset : -u_neightbor_offset;
float offset_y = uv.y + u_neightbor_offset < 1.0 ? u_neightbor_offset : -u_neightbor_offset;
vec3 pos1 = texture2D(u_texture0, uv).xyz;
vec3 pos2 = texture2D(u_texture0, uv + vec2(offset_x, 0.0)).xyz;
vec3 pos3 = texture2D(u_texture0, uv + vec2(0.0, offset_y)).xyz;
vec3 dir1 = pos2 - pos1;
vec3 dir2 = pos3 - pos1;
vec3 n = (offset_x * offset_y > 0.0 ? cross(dir1, dir2) : cross(dir2, dir1)) * u_face;
n = normalize(n);
v_wpos = pos1;
v_normal = mat3(u_matrix_for_normal) * n;
gl_Position = u_wvp * vec4(pos1, 1.0);
}
// ------------------------------------------------------------------------------------------------
// 描画
// フラグメントシェーダー
// fs_gpu_cloth_render
/*precision mediump float;*/
precision highp float;
uniform vec3 u_camera_pos; /* カメラ位置 */
varying vec3 v_wpos;
varying vec3 v_normal;
void main()
{
/* 適当なライティング */
vec3 color = vec3(0.7, 0.05, 0.025);
vec3 normal = normalize(v_normal);
vec3 ambient_light_color = vec3(0.2, 0.2, 0.2);
vec3 directional_light_dir = normalize(vec3(-1.0, -1.0, -0.5));
vec3 directional_light_color = vec3(1.0, 1.0, 1.0);
vec3 ray_dir = normalize(v_wpos.xyz - u_camera_pos);
vec3 half_vec = normalize(-directional_light_dir - ray_dir);
color *= ambient_light_color + max(dot(normal, -directional_light_dir), 0.0) * directional_light_color;
color += pow(max(dot(normal, half_vec), 0.0), 10.0) * vec3(0.35, 0.35, 0.1);
color += pow(1.0 - max(dot(-ray_dir, normal), 0.0), 2.75) * vec3(0.45, 0.45, 0.45);
/*color = normal * 0.5 + 0.5;*/
gl_FragColor = vec4(color, 1.0);
}
GPU移植の参考資料
● Cloth Simulation on the GPU
http://http.download.nvidia.com/developer/presentations/2005/SIGGRAPH/ClothSimulationOnTheGPU.pdf
● Accelerating Cloth Simulation with CUDA
http://www.andrew.cmu.edu/user/iheath/418/cloth/CUDAClothSimulatorFinalReport.html
最後に
GPU対応することで、布の高解像度化ができましたが、解像度が高くなればなるほど、制約に関する問題が顕著にあらわれてきます。
● 制約の充足に時間がかかり、不自然に伸びるゴムのような質感になってしまう。
● 布の剛性を高めるためには、Relaxationの反復回数を増やしたいところだが、コストが大きい。
● タイムステップの精度が足らなくなって、コリジョンを突き抜けてしまったりする。
実は、GPUベースのデモは、CPUベースに比べて、Relaxation回数が多くなっていたり、重力や風力の力を弱めることで、上記の問題を緩和させていたりします。
これらの改善方法は、論文などで多数考案されていますが、難易度はかなり高くなってきます。
本記事では、そこまで深くは掘り下げていませんので、ご了承ください(現段階の私の理解力ではこの辺りが限界でした……)
以上、長文となりましたがいかがでしたでしょうか。
おかしなこと言ってるなぁ、というところありましたら、是非突っ込みいただければと思います。
では、お付き合いありがとうございました!