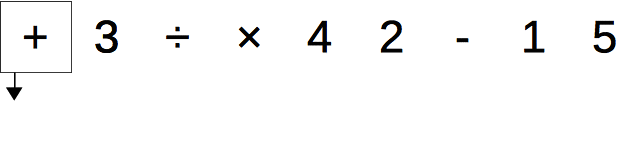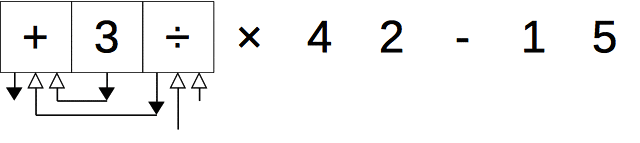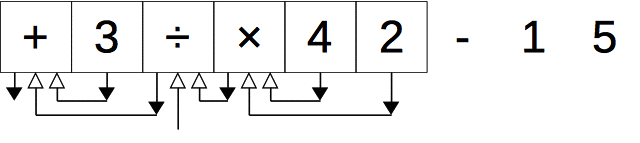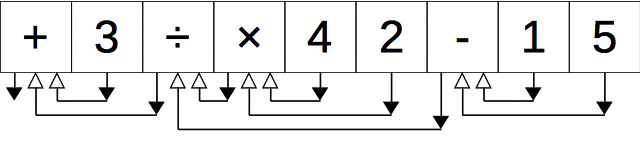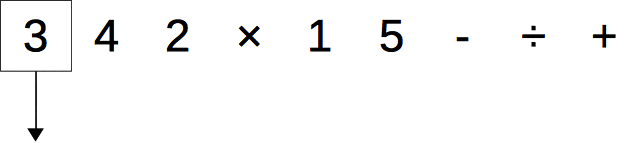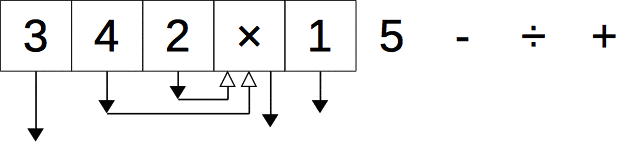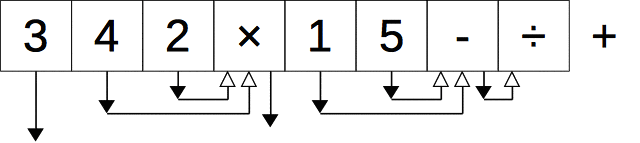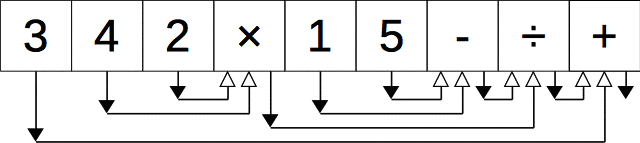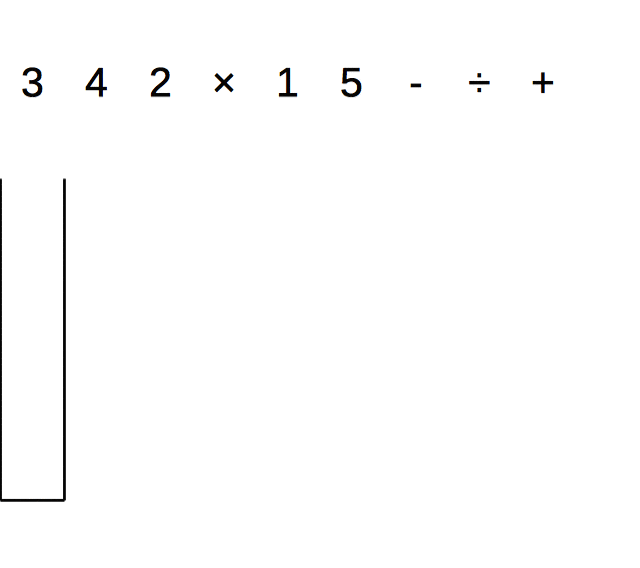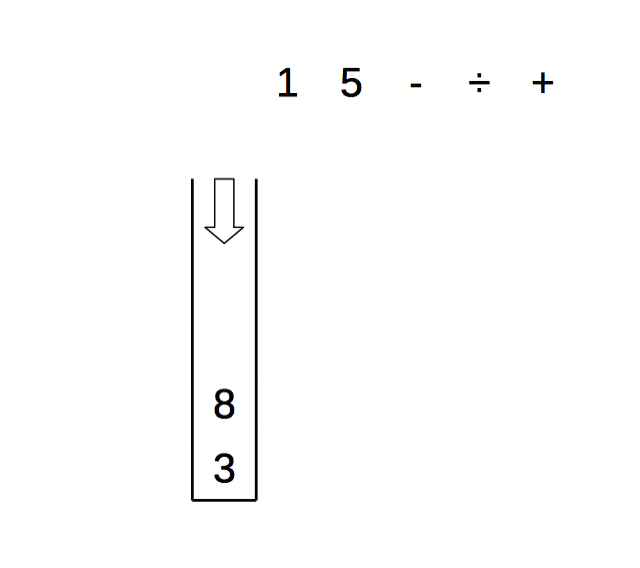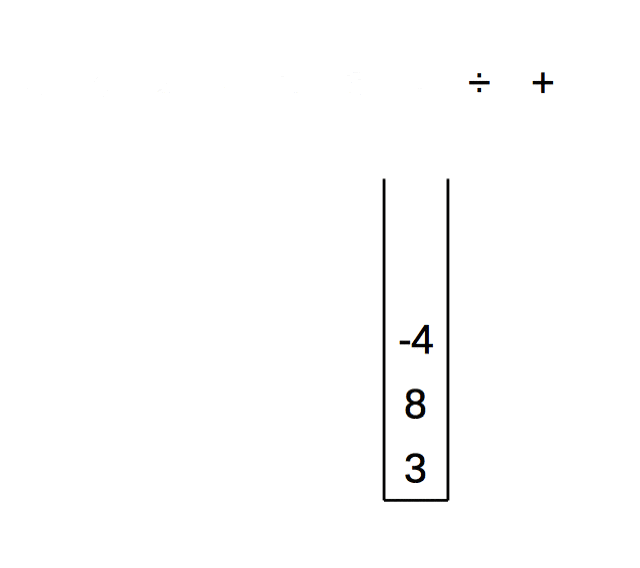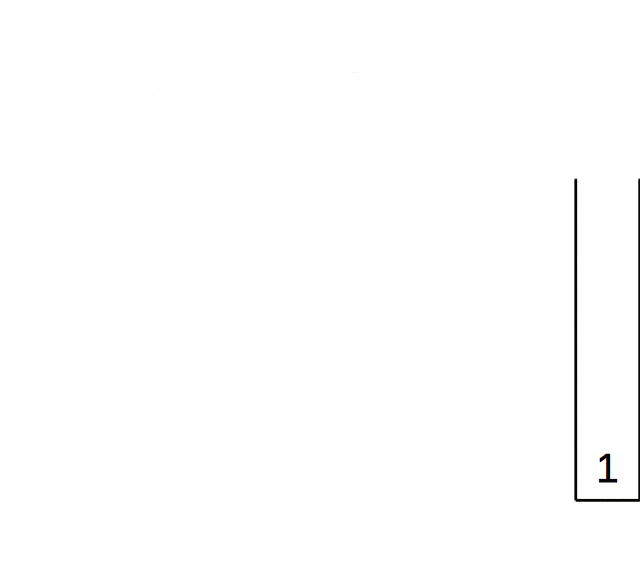逆ポーランド記法をネタにGIFアニメ作りたかっただけです。
演算子の優先順位
四則演算では加減算より乗除算のほうが優先順位が高い。例えば、下記の通り乗除算を先に評価すると解釈するのが一般的である。
-
1 + 2 × 3であれば、1 + (2 × 3) = 1 + 6 = 7と解釈される。 -
12 − 8 ÷ 4であれば、12 − (8 ÷ 4) = 12 - 2 = 10と解釈される。
演算子の結合性
また、四則演算は左結合である。例えば、下記の通り左側から結合して考えるのが一般的である。(減算が連続した場合や、除算が連続した場合に左結合でないと困ったことになる。結合法則を満たす加算や乗算は、右結合と解釈しても問題はない。)
-
9 - 3 - 1 + 6であれば、((9 - 3) - 1) + 6 = (6 - 1) + 6 = 5 + 6 = 11と解釈される。 -
16 ÷ 4 ÷ 2 × 3であれば、((16 ÷ 4) ÷ 2) × 3 = (4 ÷ 2) × 3 = 2 × 3 = 6と解釈される。
なお、べき乗は通常右結合と考える。
括弧の入れ子と木構造
演算子の優先順位や結合性により、四則演算の式は解釈されていく。そのため、優先順位や結合性に沿わない順序で計算したい場合、括弧によって計算順序を示す必要がある。例えば下記の式は、括弧があることにより除算より先に減算が計算される
-
3 + 4 × 2 ÷ (1 - 5)は3 + 8 ÷ (-4) = 3 + (-2) = 1のような順序で計算される。
上式3 + 4 × 2 ÷ (1 - 5)に対して演算子の優先順位や結合性を明示的に示すように括弧をつけると下記のようになる。
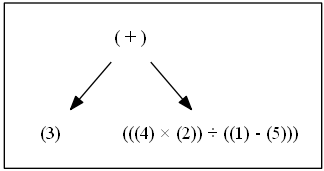
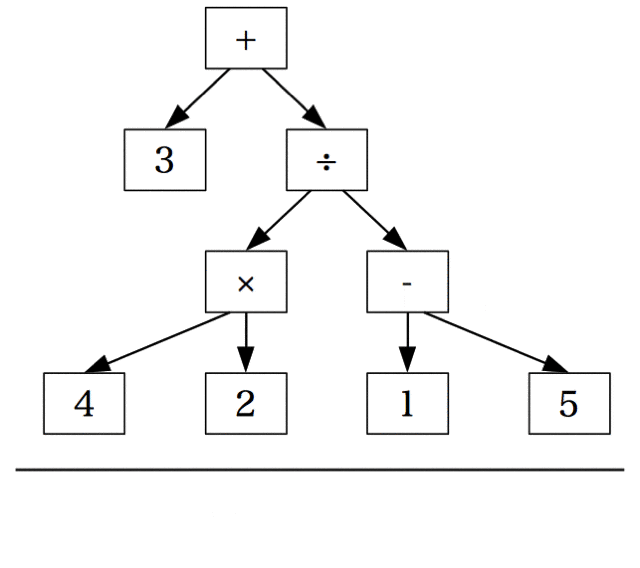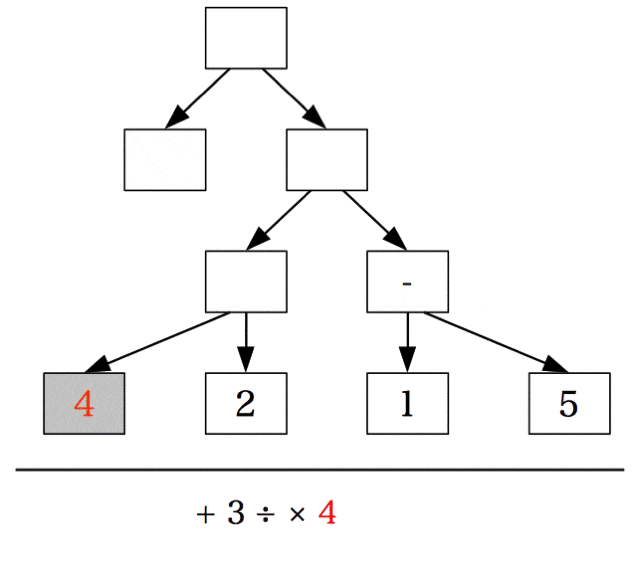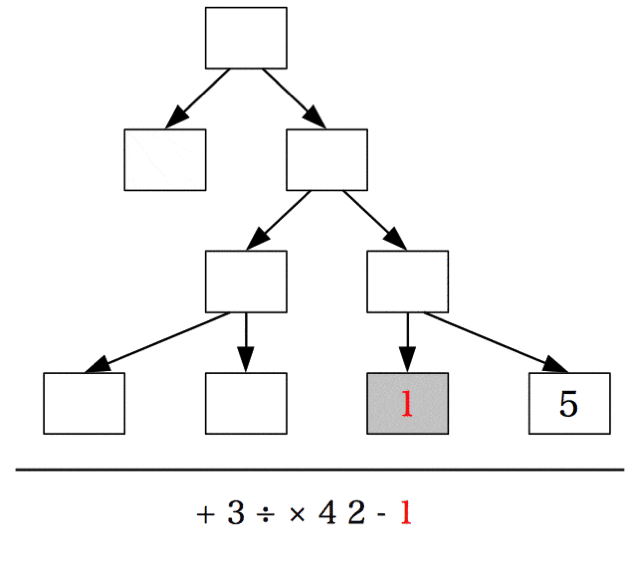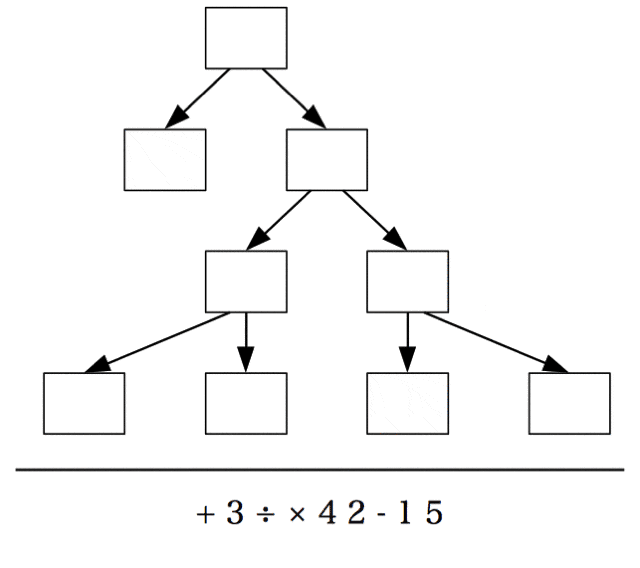
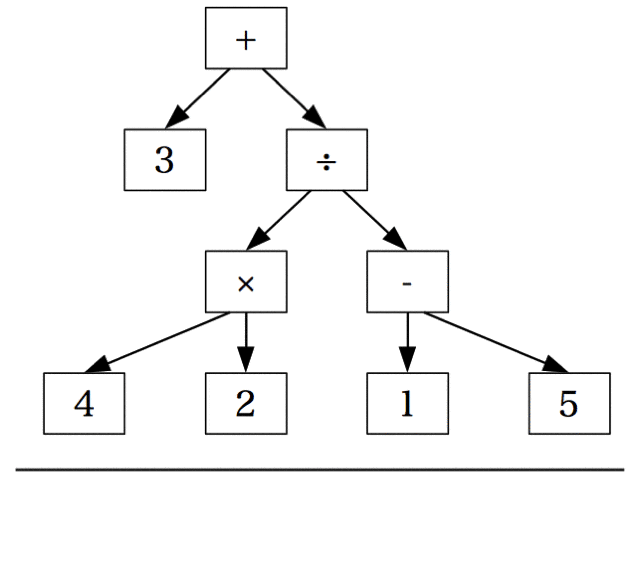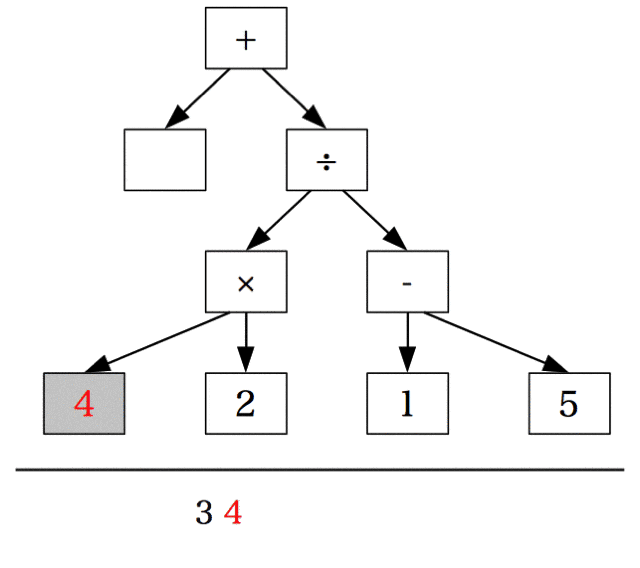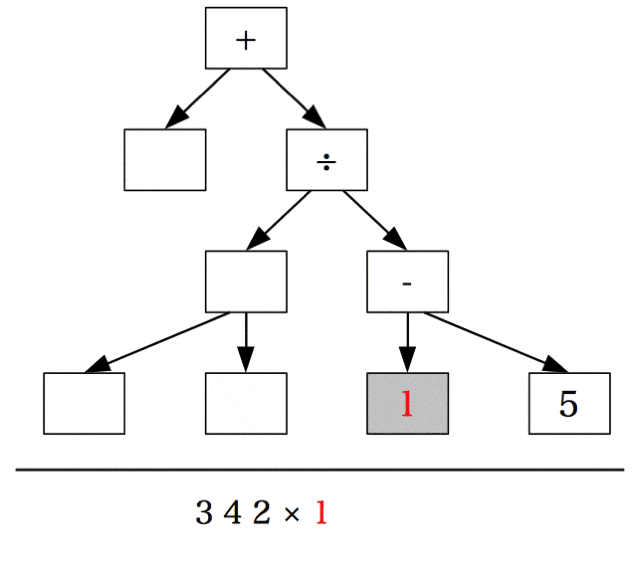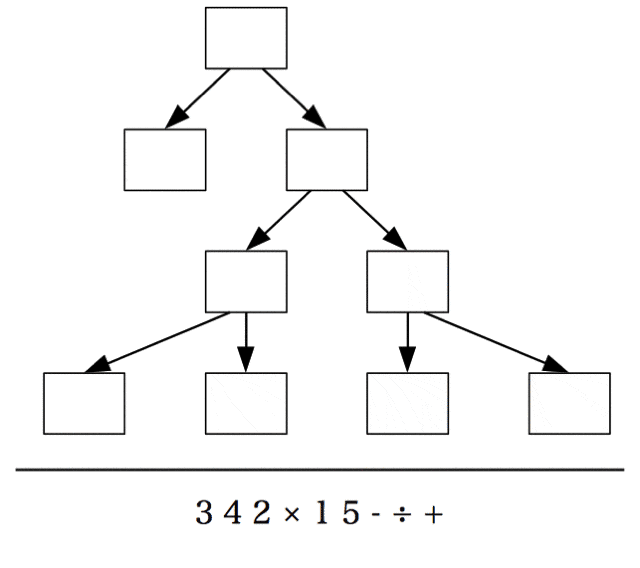
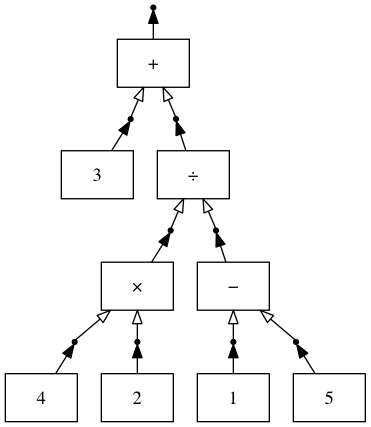
((3) + (((4) × (2)) ÷ ((1) - (5))))
括弧の入れ子だらけでぱっと見よくわからないので、木に変形して見やすくする。
まず、最も外側の括弧に注目し、それに対応する演算子(+)を持ち上げる。
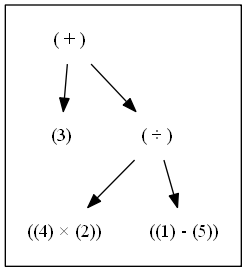
(+)の左側の子は(3)であり、括弧の入れ子はないためそのままにする。(+)の右側の子には括弧の入れ子があるので、最も外側の括弧に注目し、それに対応する演算子(÷)を持ち上げる。
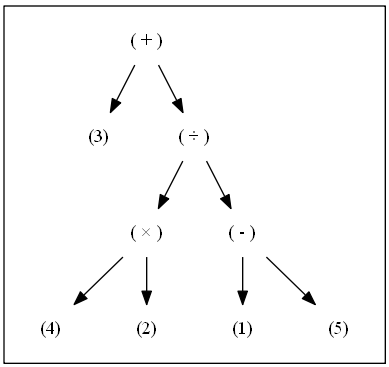
同様にして、2つの演算子(×)(‐)を持ち上げると、入れ子が解除された木構造が現れる。
木構造の走査
式の正体が木であることは分かったが、普段、式は一列に書く。つまり、私たちは木の各頂点を一列に列挙するある方法を無意識に使っていることになる。その無意識的に行っている列挙を意識的に行ってみる。
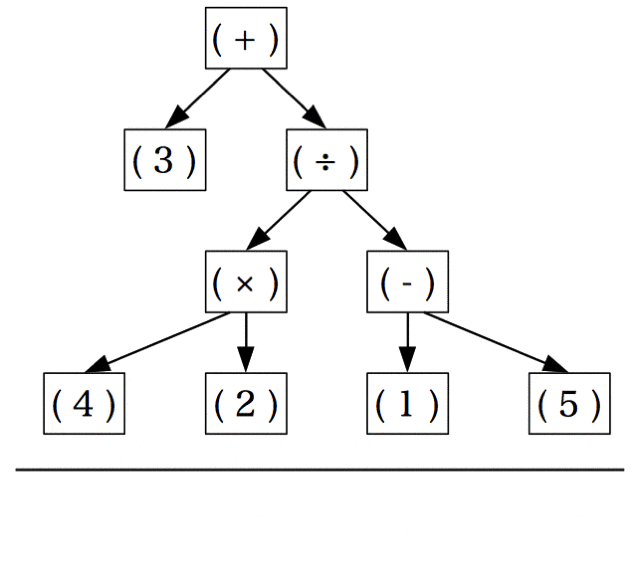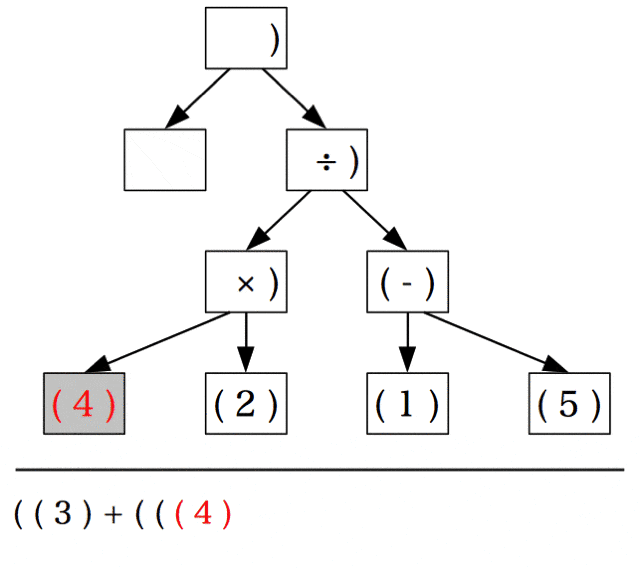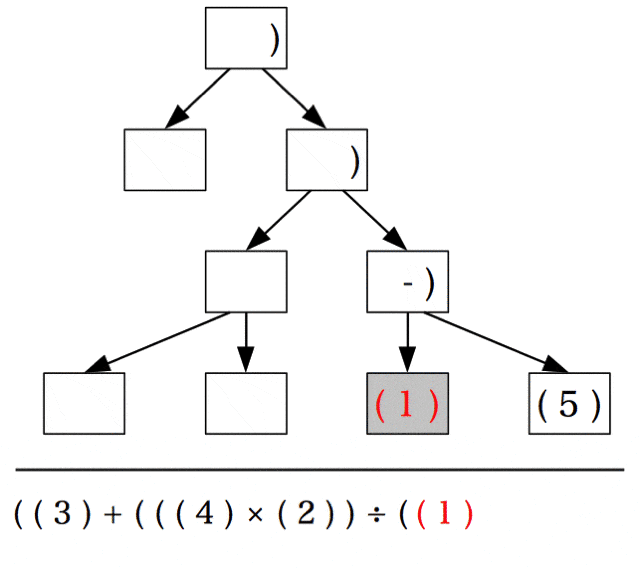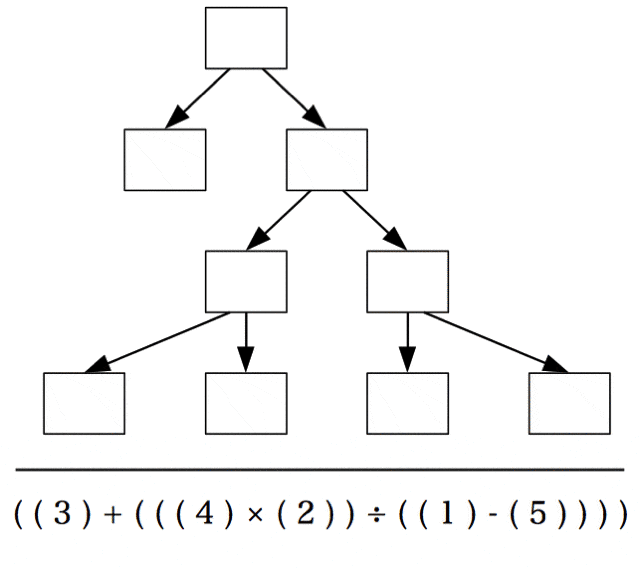
具体的には木構造の走査の間順、前順、後順の走査を((3) + (((4) × (2)) ÷ ((1) - (5))))の木に対して実行する。
間順(中置記法)
- もしあれば、左の部分木を間順走査する。
- 根ノードを調査する。
- もしあれば、右の部分木を間順走査する。
を実行した結果が下記の図。
最終的な結果の((3) + (((4) × (2)) ÷ ((1) - (5))))は、私たちが普段使う書き方だが、これを中置記法と呼ぶ。つまり、式の木を間順で走査すると中置記法で書かれた式が得られる。そして私たちが無意識に使用している木の各頂点を一列に列挙する方法とはこの間順走査のことである。
前順(前置記法)
- 根ノードを調査する。
- もしあれば、左の部分木を前順走査する。
- もしあれば、右の部分木を前順走査する。
を実行した結果が下記の図。
最終的な結果の+ 3 ÷ × 4 2 - 1 5は、演算子が被演算子の前に置かれるため、前置記法と呼ばれる。また、前置記法はポーランド記法とも呼ばれる。つまり、式の木を前順で走査すると前置記法(=ポーランド記法)で書かれた式が得られる。
各演算子の被演算子の数が一意に定まるとき、前置記法で書かれた式から元の木を一意に特定できる。そのため前置記法においては括弧、演算子の優先順位、演算子の結合性を考慮する必要がない。
一意に特定できる様子については、後で前置記法から木を再構築する絵を描くので、そこでイメージがつかめると思われる。
後順(後置記法)
もしあれば、左の部分木を後順走査する。
もしあれば、右の部分木を後順走査する。
根ノードを調査する。
を実行した結果が下記の図。
最終的な結果の3 4 2 × 1 5 - ÷ +は、演算子が被演算子の後ろに置かれるため、後置記法と呼ばれる。また、後置記法は逆ポーランド記法とも呼ばれる。つまり、式の木を後順で走査すると後置記法(=逆ポーランド記法)で書かれた式が得られる。
後置記法は前置記法と同じく括弧を必要としない。また、プログラミング演習で出題される程度には、逆ポーランド記法による四則演算の電卓は簡単に実装できる。
各記法から木への変換
前置記法と、後置記法からそれぞれ元となる木を描く。中置記法が木へ変換される絵は上に書いたので省く。
前置記法から木へ
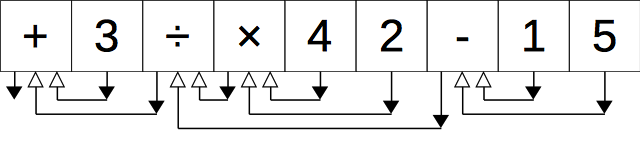
次の2つのルールで、前置記法から木を描くことができる。
- 各演算子、数値について白抜きの矢印(引数)と黒塗りの矢印(戻り値)を生やす。ただし、黒塗りの矢印を白抜きの矢印よりも左側に生やす。
- 黒塗りの矢印の頭を、その矢印から見て左にある最も近い白抜きの矢印のしっぽと結ぶ。ただし、左側に白抜きの矢印がなければどことも結ばない。
このままだとわかりづらいが、下記の図のように余っている + の戻り値(黒塗の矢印)を頂点に持ち上げると木が描けていることがよくわかる。
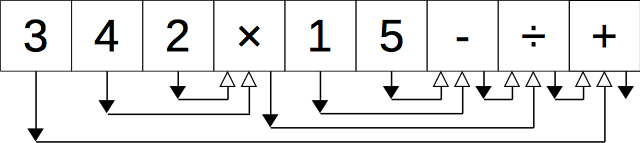
後置記法から木へ
次の2つのルールで、後置記法から木を描くことができる。
- 各演算子、数値について白抜きの矢印(引数)と黒塗りの矢印(戻り値)を生やす。ただし、黒塗りの矢印を白抜きの矢印よりも右側に生やす。
- 白抜きの矢印のしっぽを、その矢印から見て左にある最も近い黒塗りの矢印の頭と結ぶ。
+ の戻り値(黒塗の矢印)を頂点に持ち上げると元の木が描けていることがわかる。
逆ポーランド記法とスタック
スタックがあれば、逆ポーランド記法の式を先頭から評価するだけで答えが出る。
- 値であればスタックにPush
- 関数であれば、引数分スタックからPopして適用し、戻り値をPushする