はじめに
この記事は
の書き直し版です。BiboroというサイトのURLがすでに3回も変わっててやってられないので、Qiitaにまとめ直します。
またhermittaro氏のYahoo!知恵袋への過去の回答で面白いコードが
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11145530946#a359067356
あったのでこれも取り上げます
動機
今年始め
c++とvalarrayによるエラトステネスの篩
http://qiita.com/forno/items/2022d523d4e34fd86fe1
という記事がQiitaに投稿されました。
valarrayのことはすっかり忘れ去られているようだ。
歴史的経緯としては、そもそもvalarrayはベクトル型であった。当時は、ライブラリとしてベクトル演算を最適化する手法が主流であったので、valarrayもライブラリ実装による最適化を想定していた。しかし、1990年代後半から、Expression Templatesなどのテンプレートメタプログラミングを多用した最適化手法が流行り始め、valarrayは時代遅れになって放置された。誰も標準ライブラリから取り除くべきだという主張しなかったので、valarrayはそのまま残ってしまったのだ。
さて、時代は変わった。コンパイラーの最適化技術は、当時と比べてかなり進歩した。スカラー演算をまとめてベクトル演算にしたり、ループをベクトル演算にしたりといった最適化が行われるようになってきた。しかし、やはりそのような最適化には限界がある。
多くのC++コンパイラーは、Intrinsicsという、アセンブリとほぼ等しいような薄い関数としてSIMD演算を提供している。しかし、これはあまりにも特定アーキテクチャに深く結びついていて、移植性が低い。
そこで、最初からSIMDベクトル型というものがあれば、コンパイラーはベクトル演算のコードを吐く際の最適化のヒントとして使うことができる。valarrayが一周回って最新になった。
問題は、いまさらvalarrayを大幅に拡張して使うのは互換性の問題や、設計上の想定の違いから無理であろうし、やはり独立した新しいライブラリとなるべきだろう。
とあるように、なかなかvalarrayを使う人はいないので珍しい記事です。
しかし、エラトステネスの篩だったらvalarrayを使わなくても書けます。valarrayに優位性はあるのか?
比較対象
そこで
-
sieve_of_eratosthenes:std::vectorでのエラトステネスの篩 -
simple_algrism: mask方式(hermittaro氏) -
simple_algrism_mt: mask方式を私がむりやりマルチスレッド化したもの -
forno_method: @forno 氏の記事にあるstd::valarrayでのエラトステネスの篩
の速度比較をしてみます。比較するのに多少コードをいじっています
prime_vector sieve_of_eratosthenes(const prime_store_t generate_max) {//エラトステネスのふるい
if (generate_max <= 1u) return {};
prime_vector prime_num;
prime_num.push_back(2);
for (prime_store_t i = 3; i <= generate_max; i += 2) {
auto it = prime_num.begin();
const auto limit = prime_store_t(std::sqrt(i));
//調査対象数iを上回る既知の素数で割ろうとするか、既知の素数で割り切れるまでイテレータを進める
for (; it != prime_num.end() && *it <= limit && i % *it; it++);
if (i % *it) {//既知の素数で割った余りがすべて0でないならば
prime_num.push_back(i);
}
if (i == std::numeric_limits<prime_store_t>::max()) break;//iのオーバーフロー対策
}
return prime_num;
}
prime_vector simple_algrism(const prime_store_t generate_max) {
prime_vector prime_num;
auto p = std::make_unique<char[]>(generate_max + 1);
p[0] = p[1] = 1;
for (size_t j = 2; j < generate_max; j++) {
for (size_t k = j + j; k <= generate_max; k += j) p[k] = 1;
}
for (size_t j = 0; j <= generate_max; j++) if (!p[j]) prime_num.push_back(j);
return prime_num;
}
prime_vector simple_algrism_mt(const prime_store_t generate_max) {
std::vector<std::unique_ptr<std::uint8_t[]>> p;
std::vector<std::future<std::unique_ptr<std::uint8_t[]>>> threads;
const auto thread_num = std::thread::hardware_concurrency();
if (thread_num < 2) return simple_algrism(generate_max);
p.reserve(thread_num);
threads.reserve(thread_num);
for (std::uint8_t tid = 0; tid < thread_num; ++tid) {
threads.emplace_back(std::async(
std::launch::async,
[generate_max, thread_num](std::uint8_t tid) {
auto p = std::make_unique<std::uint8_t[]>(generate_max + 1);
p[0] = p[1] = 1;
for (size_t j = 2 + tid; j < generate_max; j += thread_num) {
for (size_t k = j + j; k <= generate_max; k += j) p[k] = 1;
}
return p;
},
tid
));
}
for (auto&& t : threads) {
p.emplace_back(t.get());
}
auto is_prime = [&p](std::size_t index) -> bool {
for (auto&& pn : p) if (pn[index]) return false;
return true;
};
prime_vector prime_num;
for (size_t j = 0; j <= generate_max; j++) if (is_prime(j)) prime_num.push_back(j);
return prime_num;
}
prime_vector forno_method(const prime_store_t limit) {
prime_vector prime_num;
std::valarray<bool> prims(true, limit + 1); // array of [0] to [limit]
prims[std::slice(0, 2, 1)] = false; // 0 and 1 aren't primes. (not needed)
const prime_store_t search_limit{ static_cast<prime_store_t>(std::floor(std::sqrt(static_cast<long double>(limit)))) + 1 };
for (prime_store_t i{ 2 }; i < search_limit; ++i) if (prims[i]) {
prims[std::slice(i*i, limit / i - (i - 1), i)] = false;
}
for (prime_store_t i{ 2 }; i <= limit; ++i) if (prims[i]) prime_num.push_back(i);
return prime_num;
}
結果
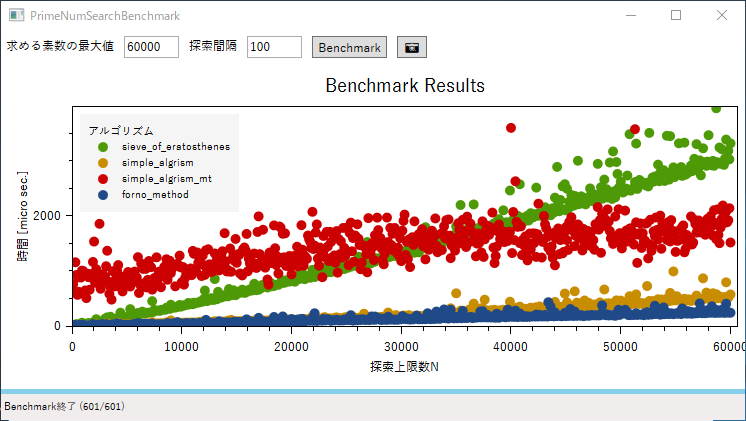
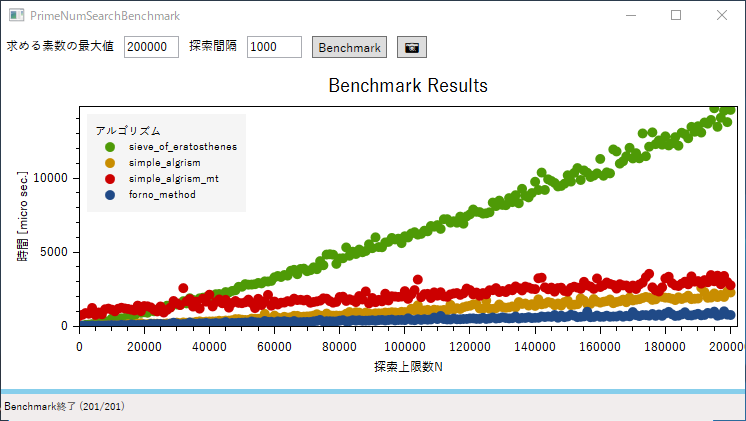
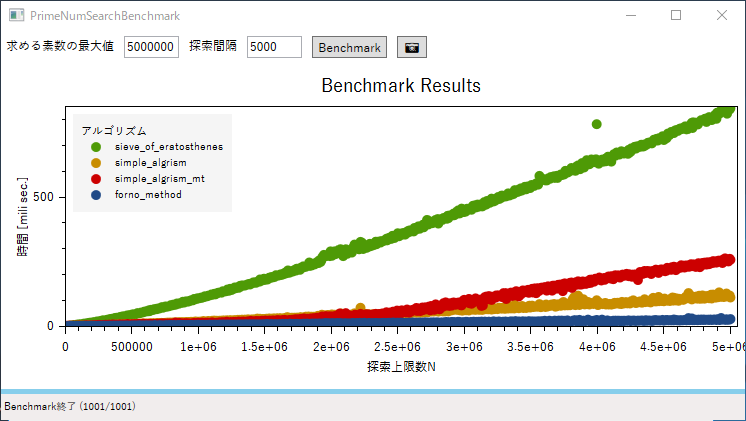
sieve_of_eratosthenesは教科書的なありきたりな実装です。一次関数的と言うよりは二次関数的な増大の仕方をしています。std::vector::push_backが遅いんでしょうね。reserveするとかやりようはあるでしょうが・・・。
simple_algrismは極めてシンプルなアルゴリズムにもかかわらず以外に高速です。
simple_algrism_mtはやっぱりマルチスレッド化が無茶だったようで、かえって遅くなりました。$ 2.5 \times 10^{6} $付近から先で急速に遅くなっています。何なんでしょうか・・・。
forno_methodが想像以上に高速でした。いや、他の実装に改良の余地が無いわけではないのですが、この比較の中では最速でした。
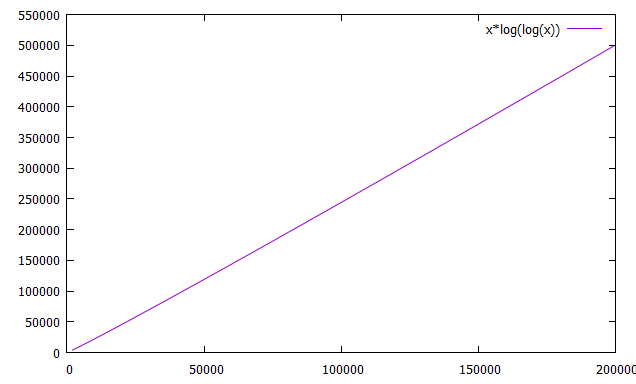
ところでエラトステネスの篩は計算量O(n loglogn)と聞いたんですが、
set xrange [0:200000]
plot x*log(log(x))
とかgnuplotで適当に作ったグラフによれば
となったんですが、これって直線・・・?私のgnuplotの使い方が違う?
結論
valarrayに優位性はあるのか?という問いですが、コードが複雑にならずそこそこ速いコードが書けるようで意外とええやん、という思いです。
ただしもうちょっとSIMD考えた新たなベクトル型が欲しいところです。
参考
検証に使ったコードは
にあります。WPFの勉強がてら作ったGUIで上のグラフは作ってます。
余談
@forno 氏の記事の直後から記事を書き始めたのですが、グラフをWPFで書こうとしてたら脱線に脱線を重ねて気がつけば11月・・・。