レンズ設計の文脈でよく出てくる点像分布関数(PSF)と、MTF曲線の具体的な数値計算の方法について最近調べていたので、それらについてまとめてみました。私はレンズ設計は専門ではなく、物理学科出身でもないので、間違っているところなどあるかと思いますが、お気づきの方はご指摘いただけると幸いです。
点像分布関数(PSF)について
**点像分布関数(Point Spread Function - PSF)**とは点光源が像面上で結像したときの、像面上における光の強度分布を表す関数です。
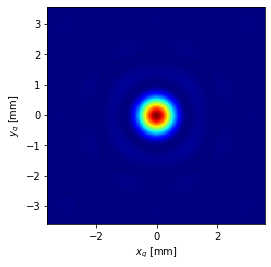
上記の画像はPSFの例です。赤色に近いほど光の強度が高いことを表します。理想的な結像では点光源は1点に集光するので、PSFはデルタ関数のような1点のみにピークを持つ関数になります。しかし、実際には収差や回折の影響で一点には集光せず、図1のようなある程度広がりを持った像が得られます。
PSFには回折の影響を考慮しない幾何光学的PSFと、回折の影響を考慮した波動光学的PSFの2種類があります。一般的にはPSFと言うと波動光学的PSFの方を指すようです。上記の例は回折を考慮した波動光学的PSFで、中心の周りにピークがもう一つあり、波打っているように見えます。
MTF曲線について
こちらの説明が分かりやすいので引用します。
MTF(Modulation Transfer Function)は、レンズ性能を評価する尺度のひとつで、被写体の持つコントラストを像面上でどれだけ忠実に再現できるかを空間周波数特性として表したものです。
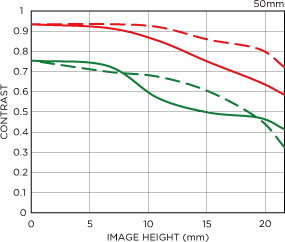
MTFは一般的には次のようなMTF曲線(MTF Curve)と呼ばれるグラフで表されます。このグラフもこちらから引用しました。
縦軸がコントラストを表し、横軸は像高と言って像面中心からの距離を表します。赤線・緑線は特定の空間周波数に対応し、実線・破線はサジタル(S)方向とメリジオナル(M)方向に対応します。ここで言うサジタルとメリジオナル方向の意味がよく分かっていないのですが、おそらく像面を極座標系$(r, \theta)$で表したときの動経方向$r$と方位角方向$\theta$に対応するのではないかと思われます。
要約すると、MTF曲線は動経方向と方位角方向の特定の空間周波数におけるコントラストを像高を変えながら表したものということになります。
MTFもPSF同様、光の回折の影響を考慮するかしないかで、幾何光学的MTFと波動光学的MTFがあります。
PSFの数値計算
PSFには幾何光学的PSFと波動光学的PSFの2種類がありました。まずは幾何光学的PSFの計算方法について見てみます。
幾何光学的PSFの数値計算
幾何光学的PSFは点光源が像面上でどのように結像するかを、回折の影響を考慮しないで表したものでした。これは**光線追跡(レイトレーシング)**を用いて比較的簡単に計算することができます。
点光源を適当な位置(一般的には無限遠?)に配置し、そこからレンズ前面に向けて多数の光線を発射します。これらの光線がレンズに当たるたびに屈折させ次の方向を計算、さらに次のレンズとの衝突位置の計算を繰り返します。最後に光線が像面と交わる位置を計算し、その位置に光が持つ放射輝度を加算します。
このようにして多数の光線に対しレイトレーシングを繰り返し、サンプル点の間は適当に補間することで、像面上における光の強度分布を得ることができます。こうして幾何光学的PSFを得ることができます。
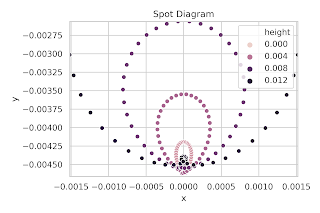
なお、光線が像面と交わった位置を表すグラフは**スポットダイアグラム(Spot Diagram)**と呼ばれます。以下の図はその例です。
回折計算
波動光学的PSFを計算するためには光を波として表現し、レンズを通過したときの回折を考慮して像面上の光の強度を求める必要があります。まずはその上で基本となる回折計算の手法について見ていきます。最後にはPythonを使って数値計算をしてみます。
ここでは以下の回折計算の方法について見ていきます。
- フレネル近似
- フラウンホーファー近似
- 角スペクトル法
光の波としての表現方法
光を波として考え、数式で表すには複素数を用いた表現が利用されます。
平面波の場合、位置$\boldsymbol{r}$, 時刻$t$における複素振幅$u(\boldsymbol{r}, t)$は
$$ u(\boldsymbol{r}, t) = A\exp[i(\boldsymbol{k}\cdot\boldsymbol{r} - \omega t + \delta)]$$
と表されます。ここで$A$は振幅, $i$は虚数単位, $\boldsymbol{k}$は波数ベクトル, $\omega$は角周波数, $\delta$は初期位相です。
球面波の場合、波源からの距離を$r$として
$$ u(r, t) = \frac{A}{r}\exp[i(kr - \omega t + \delta)] $$
と表されます。ここで$k$は波数です。
以下の計算では$\omega t$の項と$\delta$の項は影響してこないので無視されます。
回折積分
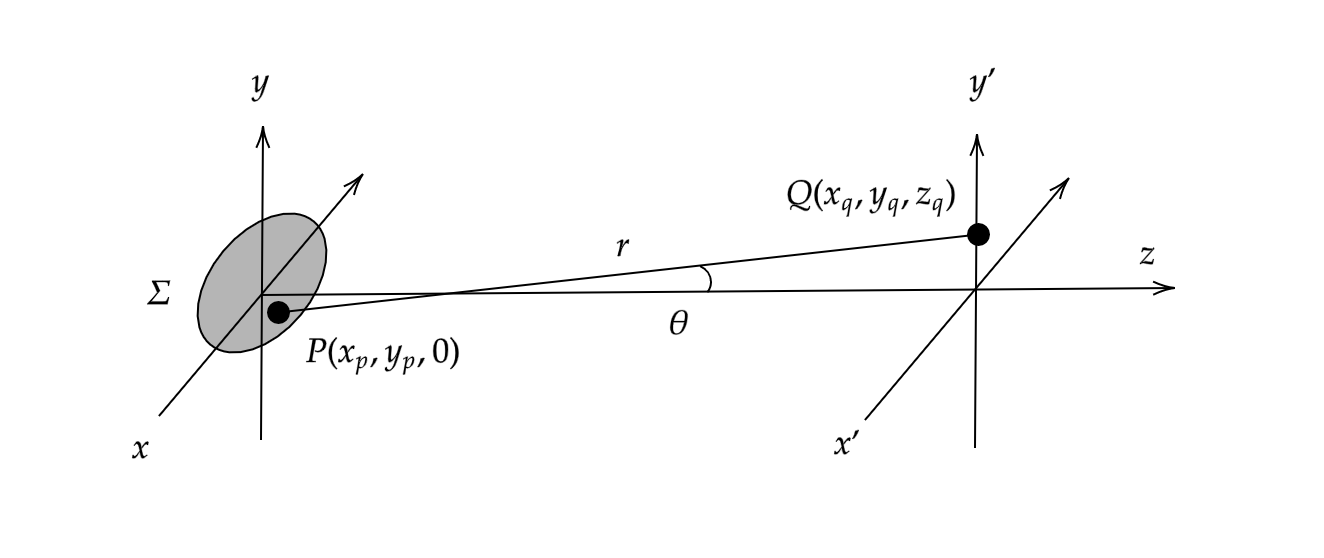
回折の計算を説明するにあたって、以下のような座標系で考えます。
$\Sigma$は開口部分を表し、$P(x_p, y_p, 0)$は$\Sigma$上の点です。$Q(x_q, y_q, z_q)$は像面上の点です。$r$は線分$PQ$の長さ、$\theta$は線分$PQ$と$z$軸のなす角を表します。
開口部分$\Sigma$を通過する平面波が、回折しながら点$Q$に到達する状況を考えます。フレネル・ホイヘンスの原理を用いると、点$Q$の複素振幅は$\Sigma$上で発生する二次波を重ね合わせたものとして表すことができます。
まずは、点$P$から点$Q$に到達する二次波の複素振幅を考えると
$$ \frac{1}{i\lambda}\frac{e^{ikr}}{r}u(x_p, y_p, 0)\cos{\theta} $$
となります。ここで$\lambda$は光の波長, $k$は波数, $u(x_p, y_p, 0)$は点$P$における複素振幅です。
点$Q$の複素振幅$u(x_q, y_q, z_q)$はこれらの二次波を$\Sigma$上全体に渡って重ね合わせたものなので
\begin{align}
u(x_q, y_q, z_q) &= \frac{1}{i\lambda}\int\int_{\Sigma} u(x, y, 0)\frac{e^{ikr}}{r}\cos{\theta}dxdy \tag{1} \\
&= \frac{z_q}{i\lambda}\int\int_{\Sigma} u(x, y, 0)\frac{e^{ikr}}{r^2}dxdy
\end{align}
となります。式変形では$\cos{\theta} = \frac{z_q}{r}$を用いました。
この積分はフレネル・キルヒホッフの回折積分と呼ばれます。これを数値積分すれば点$Q$における複素振幅が計算できるので、その絶対値の2乗を計算することで像面上の強度を得ることができます。しかし、この計算方法は開口面と像面の分割数を$N$とすると$O(N^4)$の計算量になるため、実用的ではありません。
フレネル近似
$\theta$が小さく、$\cos{\theta} \approx 1$となる状況(近軸近似)を考えます。
式1に注目すると、$\cos{\theta}$の部分は1になり、$\frac{1}{r}$は$\frac{1}{z}$と近似することができます。一方で$e^{ikr}$の項は$k = \frac{2\pi}{\lambda}$の値が大きいため、$r$を$z$で置き換えてしまうと近似の精度が良くありません。
そこで$r$を級数展開して第2項まで使うことを考えます。$r = \sqrt{(x_q - x)^2 + (y_q - y)^2 + z_q^2}$を第2項まで級数展開すると
$$ r = z_q + \frac{(x_q - x)^2 + (y_q - y)^2}{2z_q} + \cdots $$
これを回折積分の式に代入することで
$$ u(x_q, y_q, z_q) = \frac{1}{i\lambda z_q}e^{ikz_q} \int\int_{\Sigma} u(x, y, 0)e^{ik\frac{(x_q - x)^2 + (y_q - y)^2}{2z_q}}dxdy \tag{2} $$
となります。この近似をフレネル近似といい、式2をフレネル回折積分といいます。
式2の$e$の肩の中身を展開すると
$$ u(x_q, y_q, z_q) = \frac{1}{i\lambda z_q}e^{ikz_q}e^{ik\frac{x_q^2 + y_q^2}{2z_q}} \int\int_{\Sigma} u(x_p, y_p, 0)e^{-ik\frac{xx_q + yy_q}{z_q}}e^{ik\frac{x^2 + y^2}{2z_q}}dx dy \tag{3} $$
となります。式3において$f_x = \frac{x_q}{\lambda z_q}$, $f_y = \frac{y_q}{\lambda z_q}$とおくと
\begin{align}
u(x_q, y_q, z_q) &= \frac{1}{i\lambda z_q}e^{ikz_q}e^{ik\frac{x_q^2 + y_q^2}{2z_q}} \int\int_{\Sigma} u(x, y, 0)e^{-ik\frac{xx_q + yy_q}{z_q}}e^{ik\frac{x^2 + y^2}{2z_q}}dx dy \\
&= \frac{1}{i\lambda z_q}e^{ikz_q}e^{ik\frac{x_q^2 + y_q^2}{2z_q}} \int\int_{\Sigma} u(x, y, 0)e^{ik\frac{x^2 + y^2}{2z_q}}e^{-2\pi i(f_x x + f_y y)}dx dy \\
&= \frac{1}{i\lambda z_q}e^{ikz_q}e^{ik\frac{x_q^2 + y_q^2}{2z_q}} \mathcal{F}\{u(x, y, 0)e^{ik\frac{x^2 + y^2}{2z_q}}\}_{f_x = \frac{x_q}{\lambda z_q}, f_y = \frac{y_q}{\lambda z_q}} \end{align}
となり、$u(x, y, 0)e^{ik\frac{x^2 + y^2}{2z_q}}$の2次元フーリエ変換で計算できることが分かります。
フレネル近似が成り立つためには、$r$を級数展開した第3項と$k$をかけたものが
$$ \frac{k}{8z_q^3}[(x_q - x)^2 + (y_q - y)^2]^2 \ll 1 $$
を満たす必要があり、これを$z_q$に関して書き直すと
$$ z_q^3 \gg \frac{\pi}{4\lambda}[(x_q - x)^2 + (y_q - y)^2]^2 $$
となります。
フラウンホーファー近似
式3において$\frac{x^2 + y^2}{2z_q}$が十分に小さく、$e^{ik\frac{x^2 + y^2}{2z_q}} \approx 1$と近似すると
$$ u(x_q, y_q, z_q) = \frac{1}{i\lambda z_q}e^{ikz_q}e^{ik\frac{x_q^2 + y_q^2}{2z_q}} \int\int_{\Sigma} u(x, y, 0)e^{-ik\frac{xx_q + yy_q}{z_q}}dxdy \tag{4}$$
となります。この近似をフラウンホーファー近似といい、式4をフラウンホーファー回折積分といいます。
式4において$f_x = \frac{x_q}{\lambda z_q}$, $f_y = \frac{y_q}{\lambda z_q}$とすると
\begin{align} u(x_q, y_q, z_q) &= \frac{1}{i\lambda z_q}e^{ikz_q}e^{ik\frac{x_q^2 + y_q^2}{2z_q}} \int\int_{\Sigma} u(x, y, 0)e^{-2\pi i(f_x x + f_y y)}dx dy \\ &= \frac{1}{i\lambda z_q}e^{ikz_q}e^{ik\frac{x_q^2 + y_q^2}{2z_q}} \mathcal{F}\{u(x, y, 0)\}_{f_x = \frac{x_q}{\lambda z_q}, f_y = \frac{y_q}{\lambda z_q}}
\end{align}
となり、$u(x_p, y_p, 0)$の2次元フーリエ変換で計算できることが分かります。 フラウンホーファー近似が成り立つためには $$ \frac{k}{2z_q}(x^2 + y^2) \ll 1 $$ を満たす必要があり、これを$z_q$に関して書き直すと $$ z_q \gg \frac{\pi}{\lambda}(x^2 + y^2) $$ となります。
フラウンホーファー近似は開口面が十分に小さく、像を開口面から非常に離れた所で観測する場合に有効な近似と言えます。一方でフレネル近似はフラウンホーファー近似より近い所でも有効な近似です。
角スペクトル法
開口面の複素振幅$u(x, y, 0)$をフーリエ変換した$U(f_x, f_y, 0)$の逆フーリエ変換は
$$
u(x, y, 0) = \int\int U(f_x, f_y, 0)\exp[2\pi i(x f_x + y f_y)]df_x df_y
$$
です。この式は開口面の複素振幅$u(x, y, 0)$が平面波$U(f_x, f_y, 0)\exp[2\pi i(x f_x + y f_y)]$を足し合わせたものとして表現できることを表しています。
それぞれの平面波の波数ベクトル$\boldsymbol{k}$の各成分を求めると
\begin{align}
k_x &= 2\pi f_x \\
k_y &= 2\pi f_y \\
k_z &= \sqrt{k^2 - k_x^2 - k_y^2}
\end{align}
となります。$k_z$は$|\boldsymbol{k}| = k$から従います。
各平面波が$z$方向に$z_q$だけ進むと、その複素振幅は
$$
U(f_x, f_y, 0)\exp[2\pi i(x f_x + y f_y)] \exp[i k_z z_q]
$$
となります。すると像面上の複素振幅$u(x', y', z_q)$はそれらの平面波を足し合わせたものなので
\begin{align}
u(x', y', z_q) &= \int\int U(f_x, f_y, 0)\exp[2\pi i(x f_x + y f_y)] \exp[i k_z z_q] df_x df_y \\
&= \mathcal{F}^{-1}\{ U(f_x, f_y, 0) \exp[i k_z z_q] \}
\end{align}
となり、像面上の複素振幅$u(x', y, z_q)$が$U(f_x, f_y, 0) \exp[i k_z z_q]$の逆フーリエ変換で計算できることが分かります。この計算方法は 角スペクトル法(Angular Spectrum Method) と呼ばれます。
角スペクトル法ではフレネル近似やフラウンホーファー近似よりさらに開口面に近い領域での回折を計算することができます。しかも計算はフーリエ変換と逆フーリエ変換が一回ずつだけなので、高速に計算することができます。
回折の数値計算例
開口$\Sigma$を半径$r = 1~\mathrm{[mm]}$の円形開口、$\lambda = 550~\mathrm{[nm]}$、$z_q = 5~\mathrm{[m]}$として数値計算してみます。計算に使用したJupyter NotebookはGoogle Colabで見れます。
フラウンホーファー回折の数値計算
まずはフラウンホーファー近似で数値計算してみます。近似の条件について確認してみると、$x$と$y$は最大で$r$になるので
$$ z_q \gg \frac{\pi}{\lambda}r^2 \approx 5.71 $$
となります。仮定の条件を満たしていないですが、このまま計算を進めることにします。
フラウンホーファー回折は開口$\Sigma$上の複素振幅$u(x, y, 0)$を二次元フーリエ変換することで計算できます。プログラムで数値計算するには1辺の長さが$D$の計算領域を開口面を覆うようにとって$N \times N$のグリッドに分割し、それぞれのグリッド上での複素振幅を格納した配列を2次元離散フーリエ変換することで計算できます。
Pythonを用いて数値計算してみます。まずはグリッド上の複素振幅を格納した配列を用意します。
import numpy as np
import matplotlib.pyplot as plt
l = 0.55e-6 # 波長[m]
k = 2 * np.pi / l # 波数
zq = 5 # 開口面から像面までの距離[m]
N = 200 # グリッド分割数
r = 0.001 # 開口半径[m]
D = 0.05 # 開口面上の計算領域[m]
fscale = l*zq
# 開口面上の複素振幅を返す
def P(x, y):
if x**2 + y**2 < r**2:
return 1
else:
return 0
# グリッドの生成
X, Y = np.meshgrid(np.linspace(-D/2, D/2, num=N), np.linspace(-D/2, D/2, num=N))
Pv = np.vectorize(P)
Z = Pv(X, Y)
プロットしてみます。
plt.imshow(Z, extent=[-D/2, D/2, -D/2, D/2], cmap='gray')
plt.xlabel('$x_p$ [m]')
plt.ylabel('$y_p$ [m]')
白い部分が開口面に対応します。
次にこれを離散フーリエ変換するのですが、その前に計算領域に対応する像面上の領域を計算しておきます。
v = np.fft.fftfreq(N, d=D/N)
v = fscale * np.fft.fftshift(v)
# 単位は[mm]
extent= [1e3 * v[0], 1e3 * v[-1], 1e3 * v[0], 1e3 * v[-1]]
開口面上の複素振幅を離散フーリエ変換してフラウンホーファー回折像を求めます。
# 像面上の複素振幅を計算
U_fraun = np.fft.fft2(Z)
U_fraun = 1/(1.0j * l * zq) * np.exp(1.0j * k * zq) * np.exp(1.0j * k * (v**2 + v**2)/(2*zq)) * np.fft.fftshift(U_fraun)
# 強度を計算
I_fraun = np.abs(U_fraun)**2
# 正規化
I_fraun = I_fraun / np.max(I_fraun)
強度をプロットしてみます。
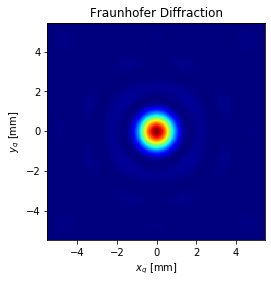
plt.imshow(I_fraun, cmap='jet', extent=extent)
plt.xlabel('$x_q$ [mm]')
plt.ylabel('$y_q$ [mm]')
plt.title('Fraunhofer Diffraction')
中心の周りにも強度のピークがあり、回折の影響が計算できていることが分かります。
フレネル回折の数値計算
最初に近似の条件を確認します。フレネル回折の近似の条件式は
$$ z_q^3 \gg \frac{\pi}{4\lambda}[(x_q - x)^2 + (y_q - y)^2]^2 $$
でした。フラウンホーファー回折の時と違って、観測面の大きさも考慮しなければならないため、少々複雑です。とりあえず観測面の1辺大きさを$l$としておきます。すると$|x_q - x| \le r + \frac{l}{2}$、$y$も同様なので、これを代入すると
$$
z_q \gg \sqrt[3]{\frac{\pi}{\lambda}(r + \frac{l}{2})^4} \approx 0.21
$$
となります。
フレネル回折もフラウンホーファー回折と同様に2次元離散フーリエ変換を用いて計算できます。
# 像面上の複素振幅を計算
U_fresnel = np.fft.fft2(Z * np.exp(1.0j * k * (X**2 + Y**2)/(2*zq)))
U_fresnel = 1/(1.0j * l * zq) * np.exp(1.0j * k * zq) * np.exp(1.0j * k * (v**2 + v**2)/(2*zq)) * np.fft.fftshift(U_fresnel)
# 強度を計算
I_fresnel = np.abs(U_fresnel)**2
# 正規化
I_fresnel = I_fresnel / np.max(I_fresnel)
強度をプロットしてみます。
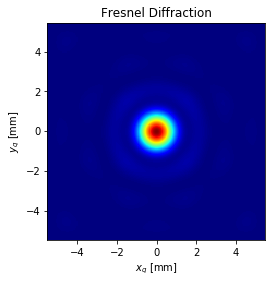
plt.imshow(I_fresnel, cmap='jet', extent=extent)
plt.xlabel('$x_q$ [mm]')
plt.ylabel('$y_q$ [mm]')
plt.title('Fresnel Diffraction')
フラウンホーファー近似のときより中心周りのピークが強くなっているように見えます。
フレネル・キルヒホッフの回折式を直接計算
フレネル・キルヒホッフの回折式
$$
\frac{z_q}{i\lambda}\int\int_{\Sigma} u(x, y, 0)\frac{e^{ikr}}{r^2}dx dy
$$
を直接数値積分して計算してみます。この方法は近似を用いないので比較的厳密ですが、計算量が圧倒的に多いため実用的ではありません。近似手法と比較したかったので計算してみました。
# フレネル・キルヒホッフの回折式の数値積分
def Uf(x_q, y_q):
r = np.sqrt((x_q - X)**2 + (y_q - Y)**2 + zq**2)
return zq/(1.0j * l) * (Z * np.exp(1.0j * k * r) / r**2).sum()
# 像面上の計算領域
X_Q, Y_Q = np.meshgrid(np.linspace(extent[0]*1e-3, extent[1]*1e-3, num=N), np.linspace(extent[2]*1e-3, extent[3]*1e-3, num=N))
# 数値積分(スケーリングは適当)
U_strict = np.vectorize(Uf)(X_Q, Y_Q)
# 強度を計算
I_strict = np.abs(U_strict)**2
# 正規化
I_strict = I_strict / np.max(I_strict)
強度をプロットしてみます。
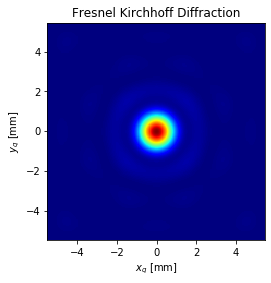
plt.imshow(I_strict, cmap='jet', extent=extent)
plt.xlabel('$x_q$ [mm]')
plt.ylabel('$y_q$ [mm]')
plt.title('Fresnel Kirchhoff Diffraction')
角スペクトル法による数値計算
最後に角スペクトル法で数値計算を行ってみます。手順としてはまず開口面の複素振幅$u(x, y, 0)$のフーリエ変換$U(f_x, f_y, 0)$を求め、次に$U(f_x, f_y, 0)$と$\exp[ik_z z_q]$をかけ合わせたものを逆フーリエ変換します。
# 開口面の複素振幅をフーリエ変換
U = np.fft.fft2(Z)
# 波数ベクトルの計算
k_x = np.fft.fftfreq(N, d=D/N) * 2 * np.pi
k_y = np.fft.fftfreq(N, d=D/N) * 2 * np.pi
K_X, K_Y = np.meshgrid(k_x, k_y)
k_z = np.sqrt(k**2 - K_X**2 - K_Y**2)
# 像面の複素振幅を計算
U_angular = np.fft.ifft2(U * np.exp(1.0j * k_z * zq))
# 強度を計算
I_angular = np.abs(U_angular)**2
# 正規化
I_angular = I_angular / np.max(I_angular)
プロットしてみます。
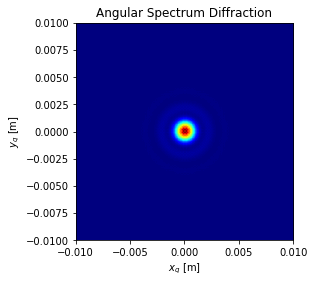
plt.imshow(I_angular, cmap='jet', extent=[-D/2, D/2, -D/2, D/2])
plt.xlabel('$x_q$ [m]')
plt.ylabel('$y_q$ [m]')
plt.title('Angular Spectrum Diffraction')
フレネル近似、フラウンホーファー近似の場合と異なり、像面の領域が計算領域と一致しているので小さく見えます。
長くなってしまったので続きは別ページに書こうと思います。
参考文献など
- 波動光学入門, 山崎正之・若木守明・陳軍, 実教出版, 2004
- 光とフーリエ変換, 谷田貝豊彦, 朝倉書店, 2012
- 回折と結像の光学, 渋谷眞人・大木裕史, 朝倉書店, 2005
- MTF曲線とは | SIGMA
- 【波動光学】波動光学入門1 - システム応答の導出
- 【波動光学】波動光学入門2 - 適当な数値計算例
- 第 4 章 フレネル・キルヒホッフの回折理論
- 5 光の回折
- 物体光の計算法
- 自由空間における光波伝搬計算手法とその応用