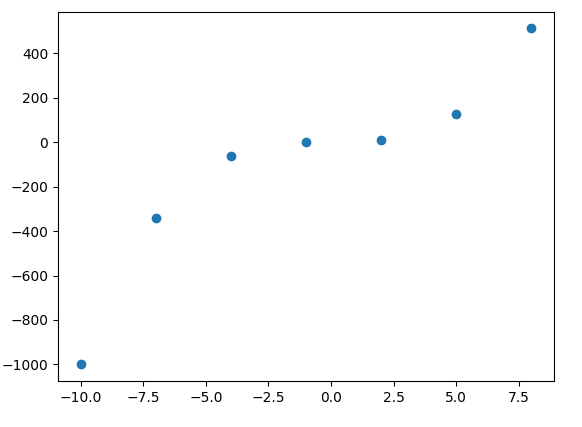
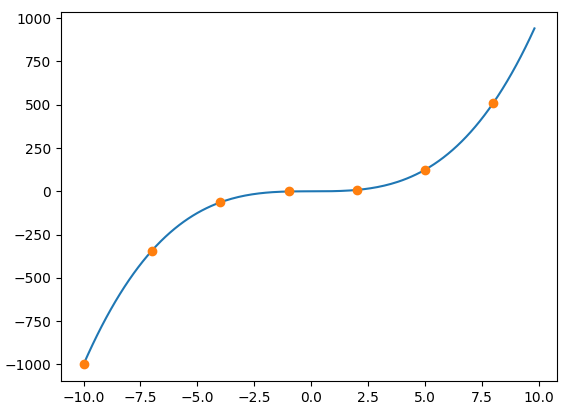
大学の授業でLagrange補間を知ったのでPythonで実装してみました。
関数の補間とは
関数の補間とは離散的に得られている点から、それらをつなぐ連結的な関数を導き出すことです
【離散的】
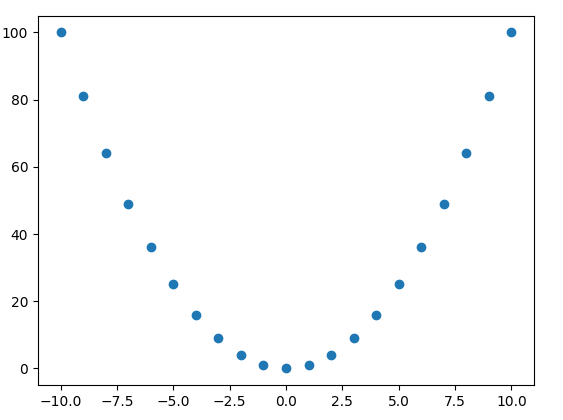
【連続的】
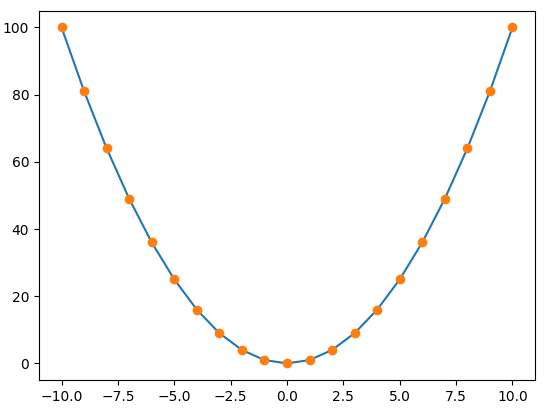
Lagrange補間法とは
j=0,1,2…nに対してxjとf(xj)の値を既知のデータ点として設定した場合
l_j(x) = \frac{(x-x_0)(x-x_1)…(x-x_{j-1})(x-x_{j+1})…(x-x_n)}{(x_j-x_0)(x_j-x_1)…(x_j-x_{j-1})(x_j-x_{j+1})…(x_j-x_n)}\\
P_n(x) = \sum_{j=0}^{n}f(x_j)l_j(x)
という風になります。大事なところはlj(x)を求める際、ｊ番目を飛ばすということです。（0になってしまうから）
PythonでLagrange補間法
以下のようになります。
Lagrange.py
import numpy as np
import matplotlib.pyplot as plt
def lagurange(x,xp,fx):
results = [];
for l in range(len(x)):
if(x[l] in xp):
results.append(fx[np.where(xp==x[l])])
else:
result=0
for j in range(len(xp)):
lag = lx(x[l],j,xp)
result += fx[j]*lag
results.append(result)
return results
def lx(x,j,xp):
numerator,denominator = 1,1
for i in range(len(xp)):
if(i!=j):
numerator *= x-xp[i]
denominator *= xp[j]-xp[i]
return numerator/denominator
def main():
xp = np.arange(-10,10,3)
fx = xp**3
x = np.floor(np.arange(-10,10,0.1)*10)/10
y = lagurange(x,xp,fx)
plt.plot(x,y)
plt.plot(xp,fx,"o")
plt.show()
if __name__ == '__main__':
main()
原始的に何も考えずにそのまま実装したのでもっと効率の良い書き方があると思います。
このプログラムでは関数y=x^3のxを3刻みのデータで既知とし、x=-10~10範囲で0.1刻みでLagrange補間を行っています。
既知のデータ点
Lagrange補間後
しっかりとy=x^3の近似ができていますね。