応用数学
(1)線形代数
(1.1)概要
- 線形代数とはベクトルや行列を扱う学問で、主に画像処理や統計の分野で使われている。
- ベクトルとは縦または横に数字を並べ、ひとまとめにしたもの。「大きさ」と「向き」を表し、矢印で表現することができる
- 行列とは数字を縦と横に並べ、ひとまとめにしたもの（ベクトルは縦または横が一列の行列である）。ベクトルの変換に使われる。
- 普段我々が使っていて、ベクトルや行列を構成する一つ一つの数字をスカラーと呼ぶ。ベクトルや行列の係数となることができる。
#####(1.2)固有ベクトルと固有値
- 線形代数では、あるベクトルに対して行列をかけることで別のベクトルに変換させる線形変換と呼ばれる方法がよく使われる。
- 線形変換を行ったとき、向きが変わらず大きさだけ変化する場合がある。このとき、向きが変わらなかったベクトルのことを固有ベクトルと呼び、係数のことを固有値と呼ぶ。
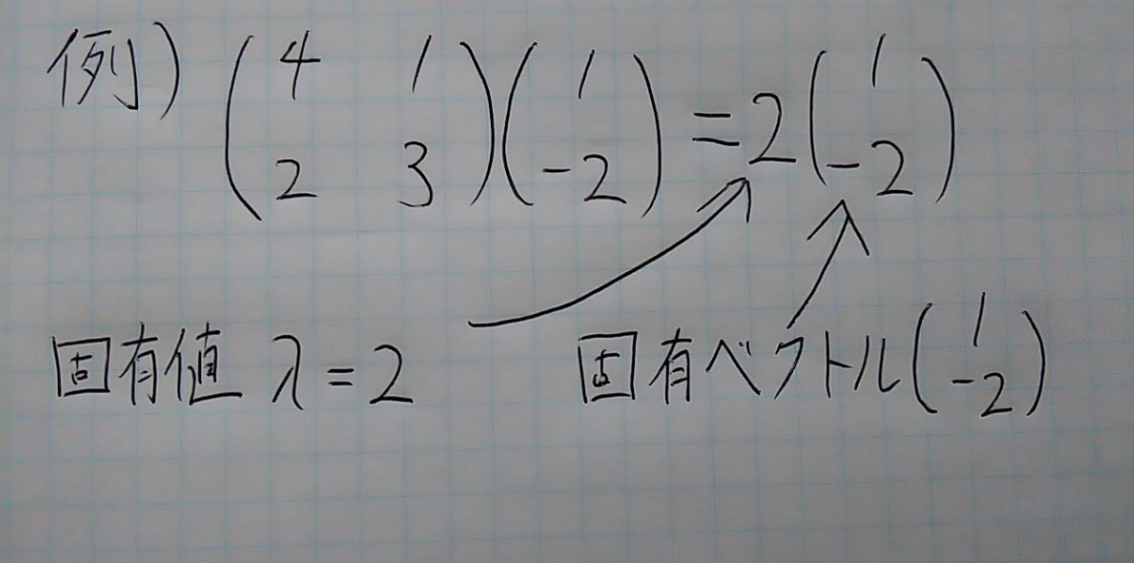
#####(1.3)固有値分解
- スカラーを正方形に並べて作られた行列Ａが固有値λ1,λ2...と固有ベクトルv1,v2...を持っているとする。固有値を対角線上に並べた行列をX、固有ベクトルを並べた行列をVとすると、AV＝VXが成り立ち、A＝VXV^-1と変形できる。このように正方形の行列Aを3つの行列V、A、V^-1の積に変換することを固有値分解という。固有値分解により行列の累乗の計算が容易になるという利点がある。
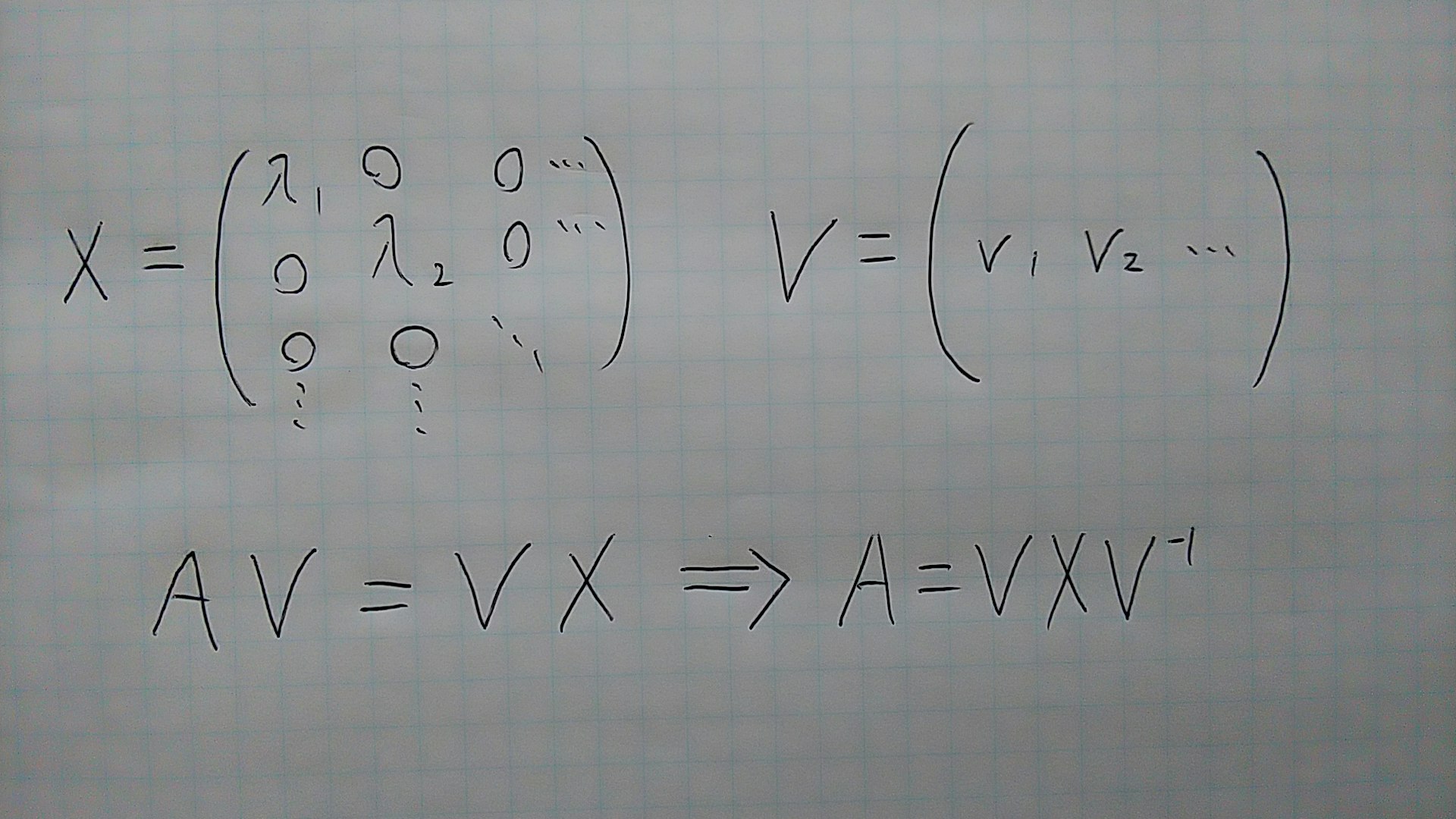
#####(1.4)特異値分解
- 固有値分解は正方形に並べて作られた行列にしかできないが、正方形ではない行列でも似たような形に変換することはできる。ある行列Aとあるベクトルv,u、スカラーxに、Av＝xu、(Aの転置行列)u＝xvが成り立つ場合、A＝USV^-1が成り立つ。これを特異値分解という。
(2)確率・統計
(2.1)概要
- 確率には2種類あるとされている。
- 1つ目は頻度確率(客観確率)と呼ばれ、ランダムな事象が発生する頻度を確立として考えるもの。
- 2つ目はベイズ確率(主格確率)と呼ばれ、観測された事象以外の情報も考慮して推測された主観的な確率のことをいう。
(2.2)条件付き確率
- お互いに因果関係のない事象X=xとY=yが同時に発生する確率を同時確率と呼び、P(X=x,Y=y)=P(X=x)P(Y=y)=P(Y=y,X=x)と表す。
- ある事象X=xが起きたという条件でY=yとなる確率を条件付き確率と呼び、P(Y=y|X=x)=P(Y=y,X=x)/P(X=x)と表記する
(2.3)ベイズ則
- 条件付き確率に関して、P(X=x|Y=y)P(Y=y)=P(Y=y|X=x)P(X=x)が成り立つ。これをベイズ則という。
- 例)ある街の子供たちは毎日1/4の確率で飴玉をもらうことができ。1/2の確率で笑顔になる。その街の子供たちが笑顔でいる確率は1/3である。笑顔な子供が飴玉をもらっている確率を求めよ。
- ベイズ則は迷惑メールのフィルタリング機能などに使われている。
(2.4)確率変数と確率分布
- 確率変数とは事象と結びつけられた数。
例）さいころの目、コインの表裏(表を1、裏を0にする)など - 確率分布とは各事象が発生する確率のことをいう。
(2.4)期待値
- ある確率分布における確率変数の平均値。確率変数と確率の積の和で表す。
(2.5)分散と共分散
- 分散とは各データと期待値のズレを平均したもの。分散が大きければデータのばらつきが大きい、分散が小さければデータのばらつきが小さいことを示す。
- 共分散とは2組のデータ間の偏差の積を平均したもの。共分散が正の値の場合は似た傾向、負の値の場合は逆の傾向、ゼロに近ければ関係性が低いということがわかる。
(2.6)確率分布
-
(2.6.1)ベルヌーイ分布
- 事象が2種類しかない場合の確率分布。2種類の事象が同じ確率でない場合でも扱うことができる。
- 例）コイントス
-
(2.6.2)マルチヌーイ分布
- 事象が複数ある場合の確率分布。ベルヌーイ分布と同様に各事象の起こる確率が等しくない場合でも扱うことができる。
- 例）さいころ
-
(2.6.3)2項分布
- ベルヌーイ分布を複数回繰り返した場合の分布。
- ベルヌーイ分布を複数回繰り返した場合の分布。
-
(2.6.4)ガウス分布
- 横軸を確率変数、縦軸を確率密度としたとき、釣り鐘型の形になる分布。正規分布とも呼ばれる。
- 正規分布は平均を0、分散が1の分布に変換することができる。これを標準化と呼ぶ。機械学習の際にデータの前処理で標準化を行うことで、モデルの制度がよくなることが知られている。
(3)情報理論
(3.1)自己情報量
- 確率Pで起こる事象で得ることができる事故情報量を-log(P)で表す。対数の底が2のときは単位がbit、ネイピア数(e)のときは単位がnatとなる。
- 直感的には、発生する確率が低い事象のほうが情報量が多い。
(3.2)シャノンエントロピー
- 自己情報量の期待値をシャノンエントロピー(平均情報量)という。
(3.3)カルバック・ライブラー・ダイバージェンス
- カルバック・ライブラー・ダイバージェンス(KL情報量)とは同じ事象・同じ確率変数における異なる２つの確率分布がどの程度似ているかを示す尺度。
- 2つの確率分布が似ていると値は0に近づく。似ていないと値は大きくなる。
(3.4)交差エントロピー
- 交差エントロピーはH(P,Q)のように表記され、Q(x)についての自己情報量がP(x)の分布に基づいているとき、複数の事象の中からひとつの事象を特定するために必要なビット数を平均したもの。つまり自己情報量を他の確率分布を元にした時の期待値。
- 機械学習やディープラーニングでは誤差関数として利用され、交差エントロピーを最小にするようにパラメータの調整が行われる
