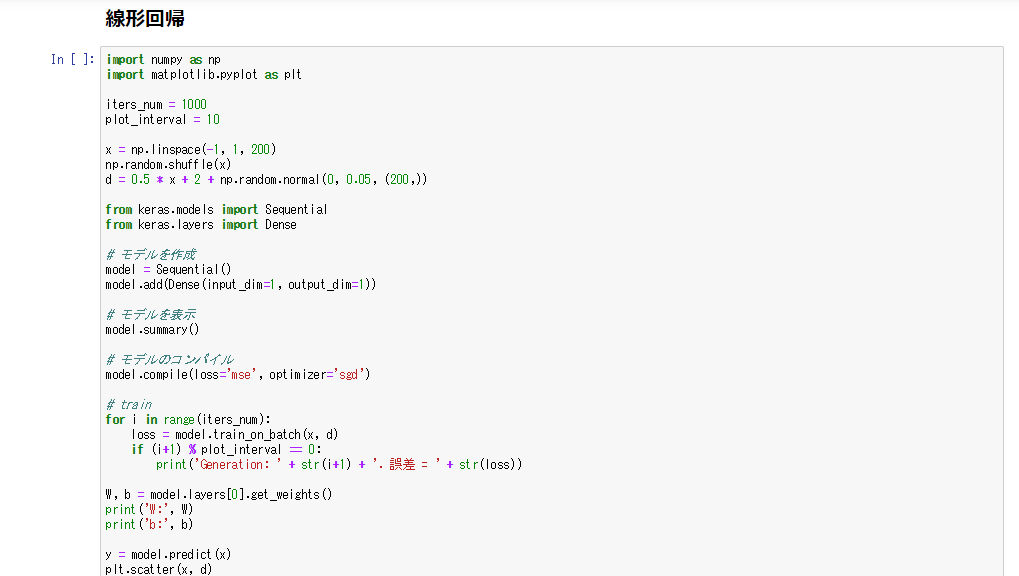
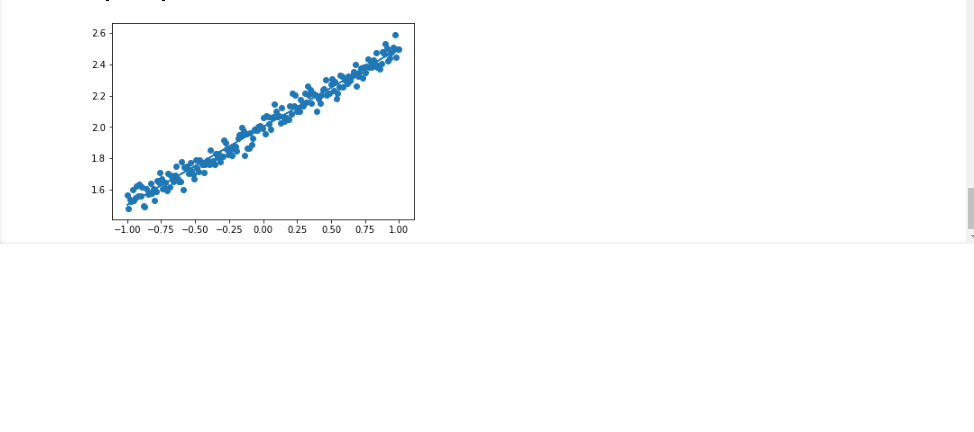
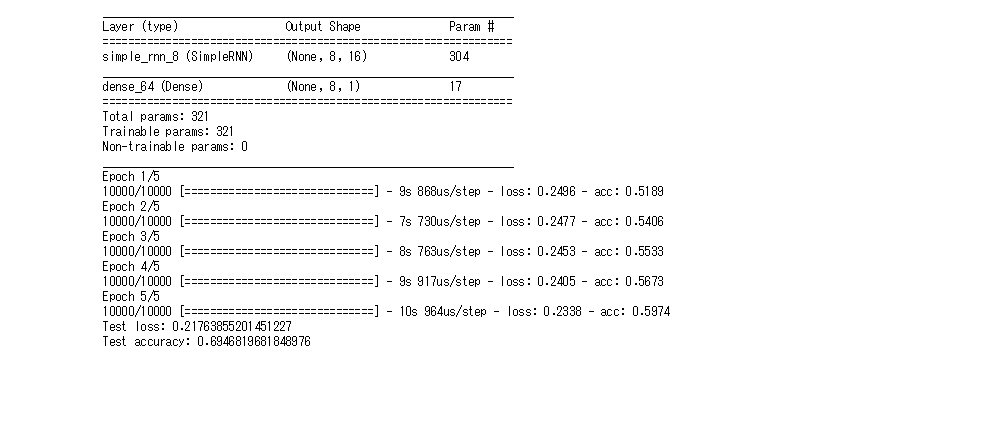
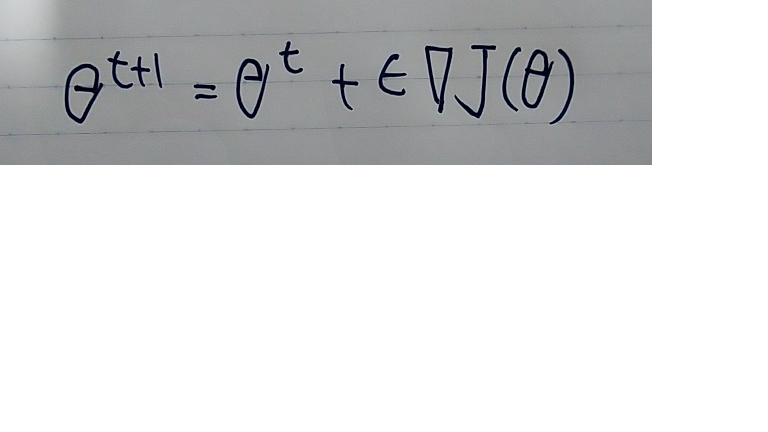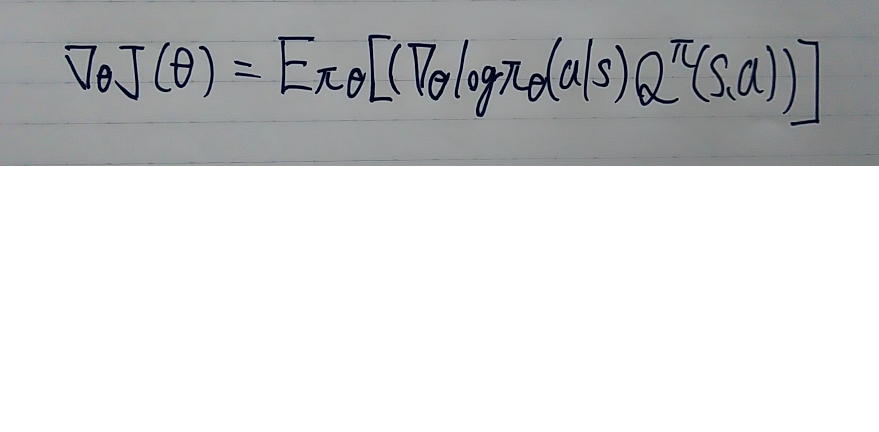Keras
- kerasはTensorFlowをより簡易化したライブラリである
- Variablesで変数の定義やプレースホルダー設定が必要ないので、シンプルにコードを書くことができる
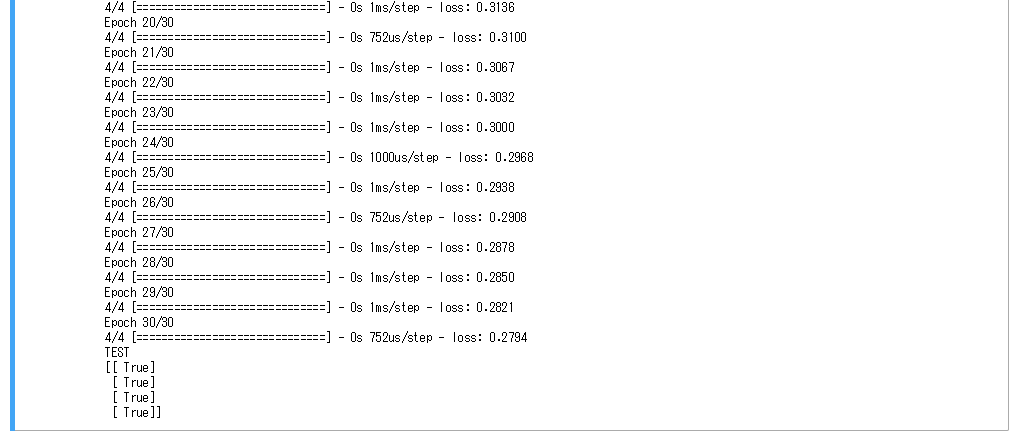
OR回路
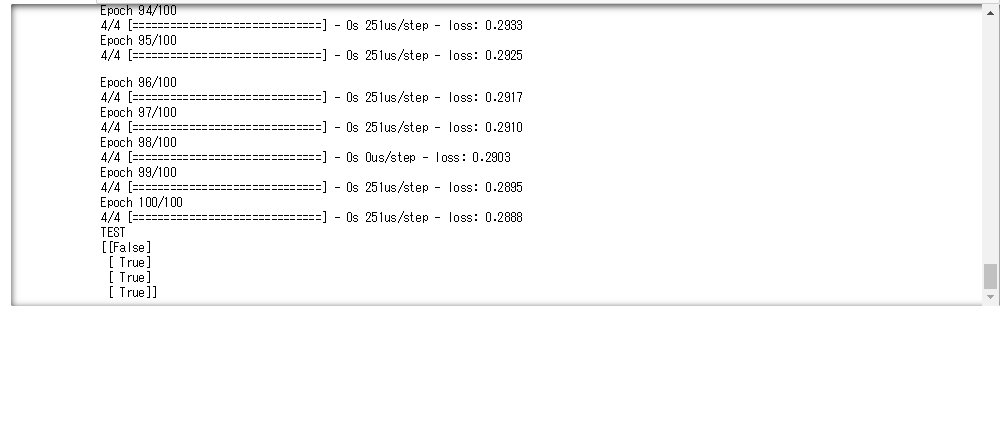
- ランダムシードを0から1に変更すると、学習の精度が落ちていることが分かった。ランダム要素を変えるだけで精度の良しあしが変わる
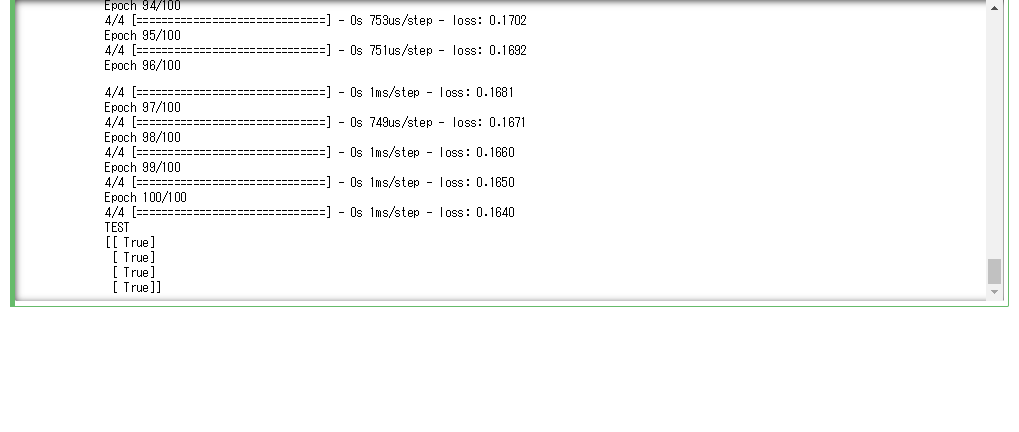
- エポック数を30から100に変更することで、最終的な誤差が少なくなることが確認できた。しかし、エポック数を増やすと計算に時間がかかる、過学習を起こすなどのデメリットもある
OR回路をAND回路に変更すると学習がうまくいくが、XOR回路にすると学習がうまくいかない。これはXOR回路が非線形なためである。これを解消するには活性化関数を使う、多層にするなどを行うとよい
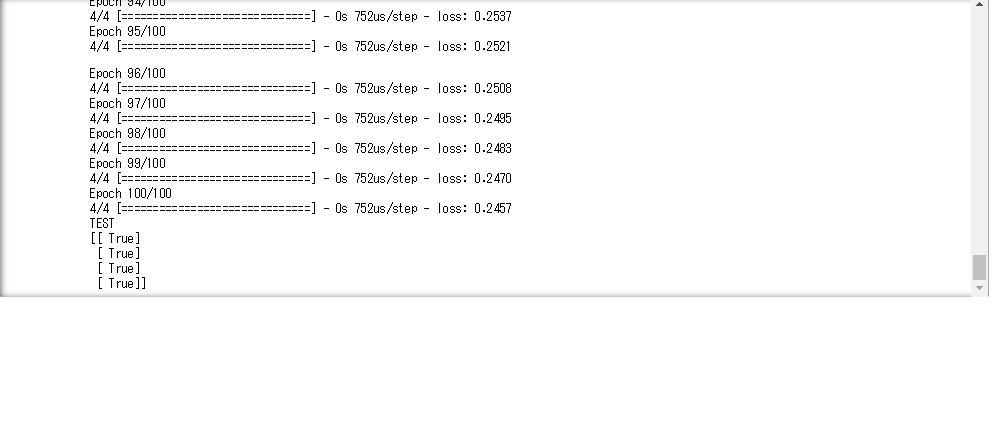
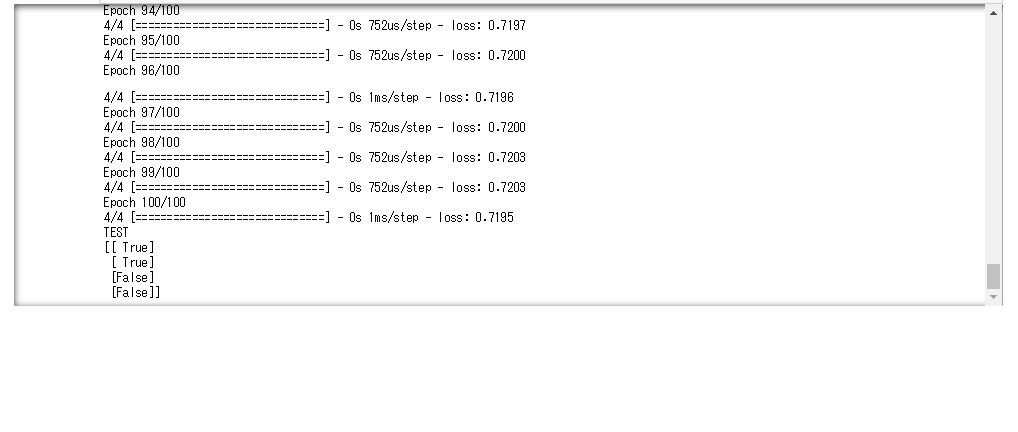
バッチサイズを1から10に変えると一回の計算速度が速くなっていることが確認できる
irisデータの分類
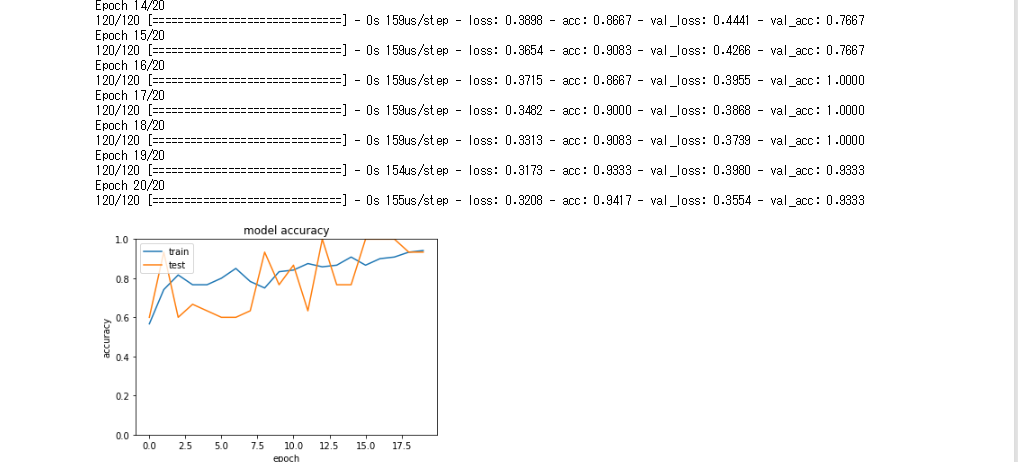
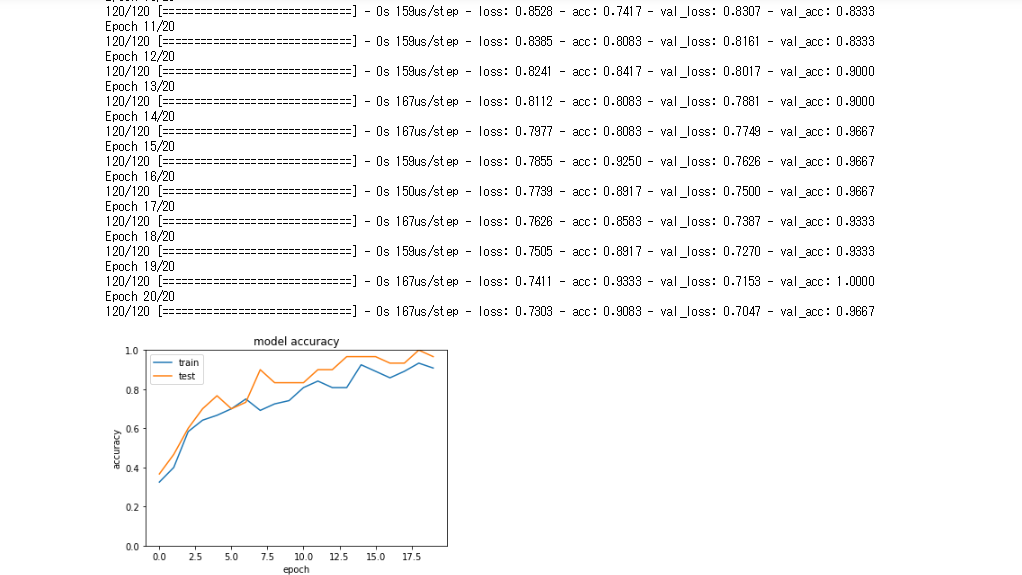
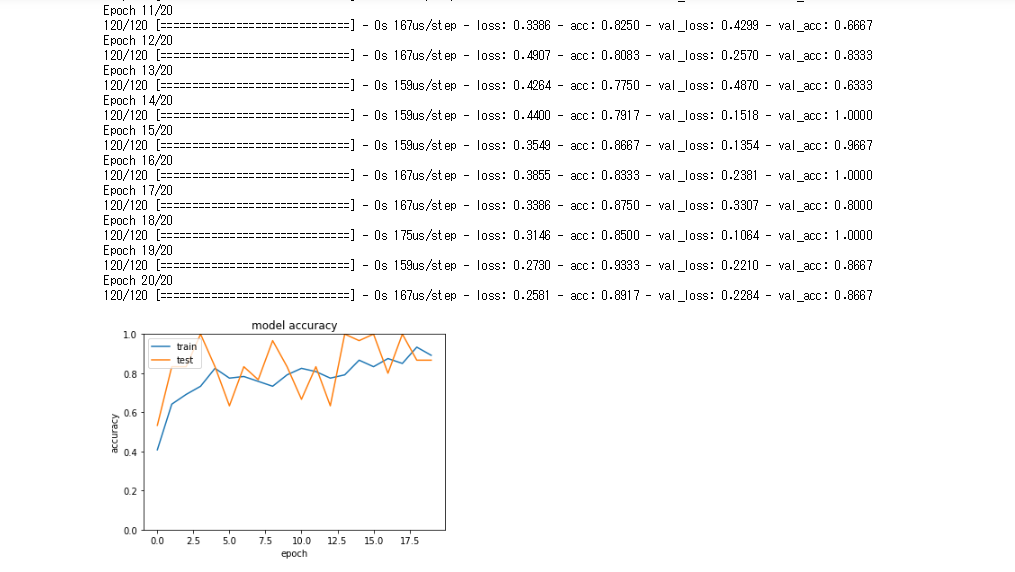
- 活性化関数にrelu関数を使用したニューラルネットワークでirisデータの分析を行う
- 活性化関数をシグモイド関数にすると、同様に良い結果を得ることができた。層が深いニューラルネットワークにするとシグモイド関数のほうが精度が悪い場合が多い
- 確率的勾配降下法の学習率を0.1にした場合、早い段階で精度が高くなっていることが確認できる(初期値は0.01なのでSGDをインポートしてcompileの引数に渡すことで学習率を変える)
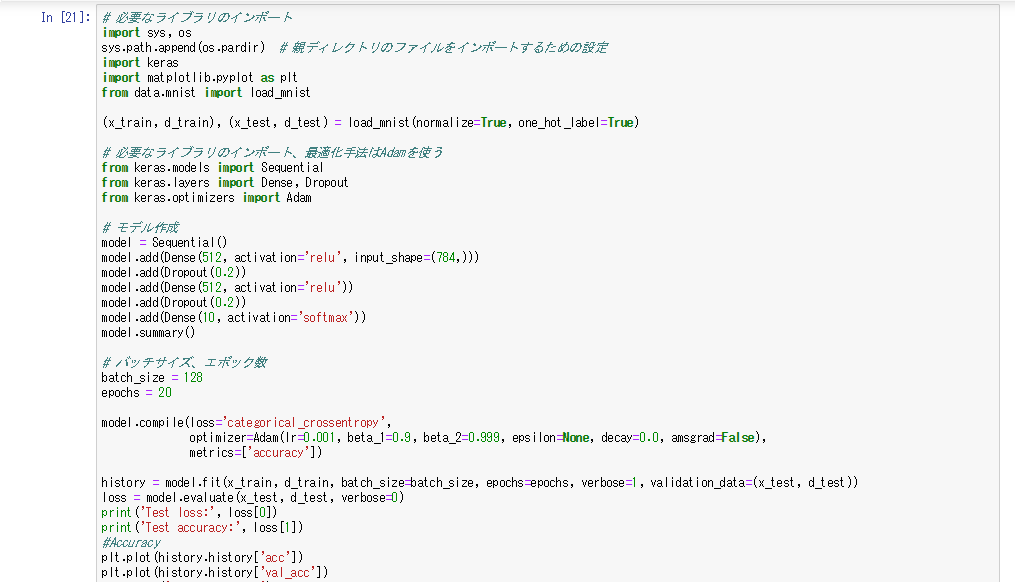
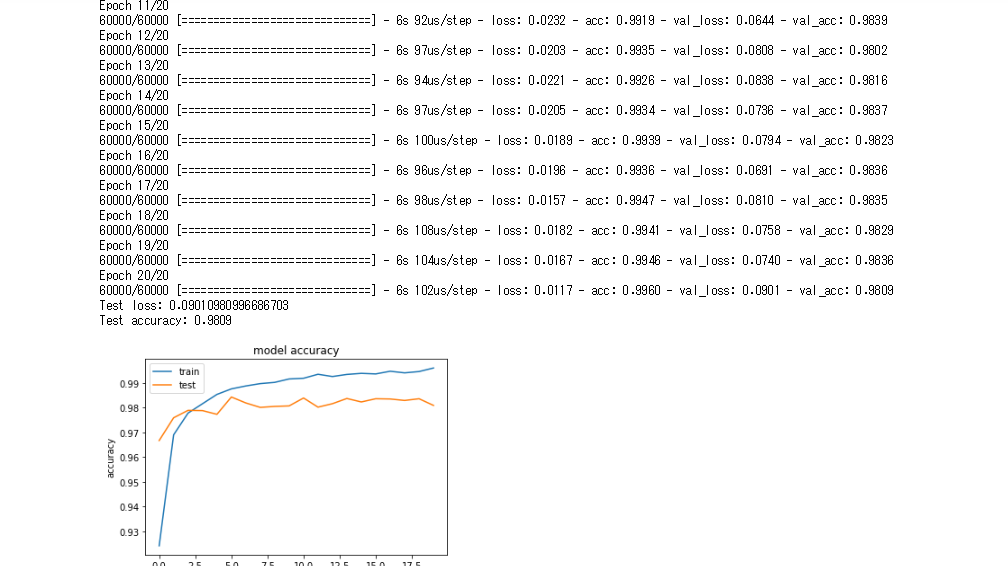
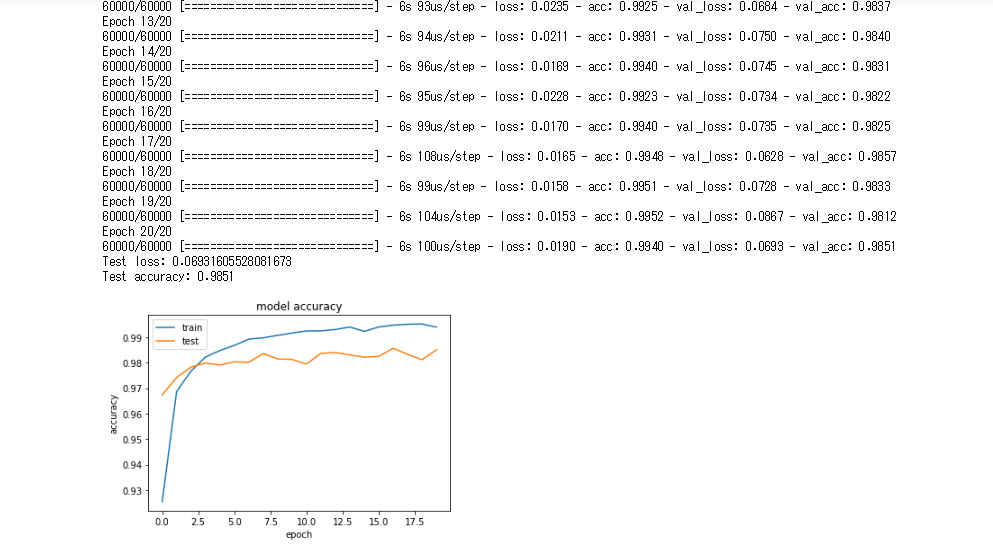
mnist(分類)
- ワンホットベクトルをFalseにするとエラーが発生する。これは誤差関数にカテゴリカルクロスエントロピーを使う場合はワンホットベクトルを出力層の出力としなければならないためエラーが起きた。そこで誤差関数にスパースカテゴリカルクロスエントロピーを使うことでエラーを起こさず学習を行うことができる。分類をワンホットベクトルで行うか、そうでないかで使用する誤差関数を変える必要がある
- Adamの学習率を0.001から0.01にあげると学習精度はあまり変わらないことを確認した
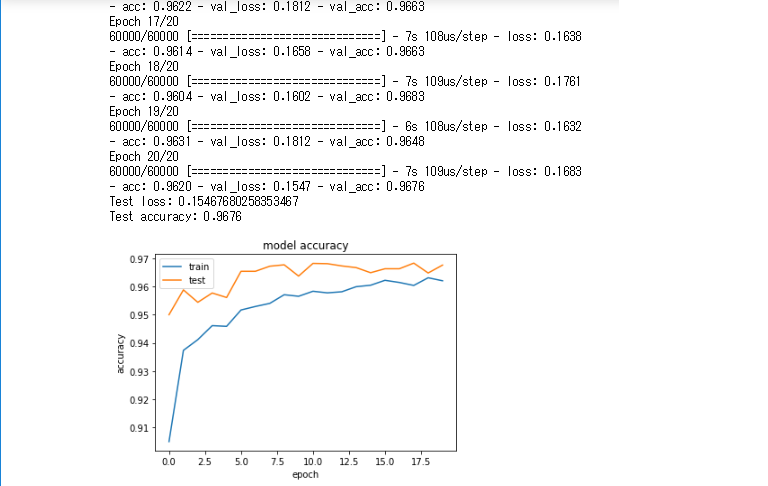
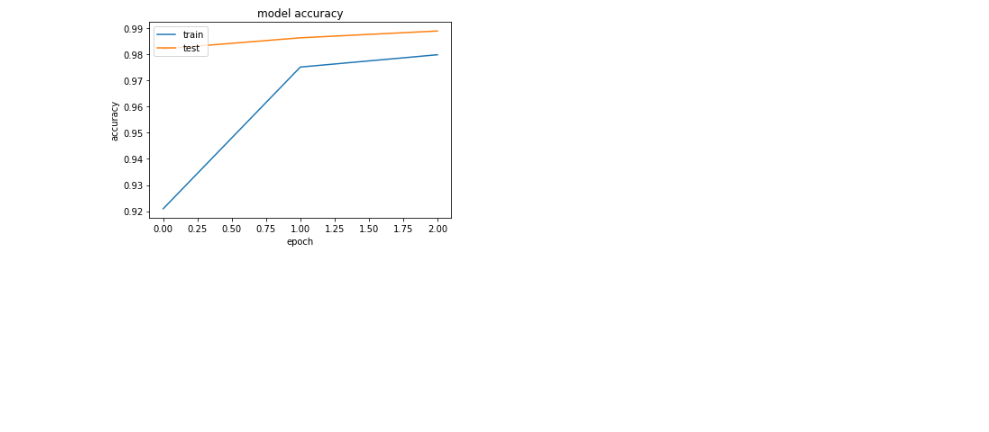
mnist(CNN)
- kerasでは重み行列の列数、行数を手動で設定する必要がない
- TensorFlowと同様にpaddingをsameとすると入力と出力のサイズを一致させることができる
cifer10
- 車や犬などの画像のデータセットを分類する問題
- 正解ラベルがワンホットベクトルではないため、必要に応じてワンホットベクトル化する必要がある
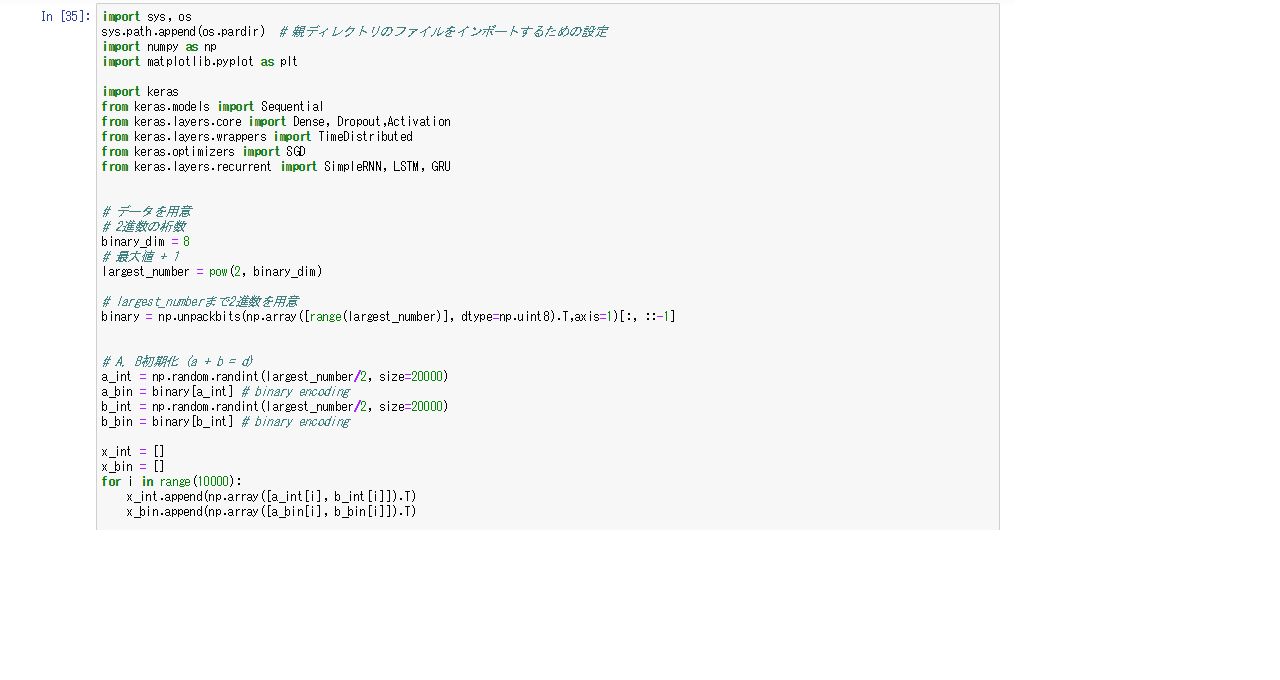
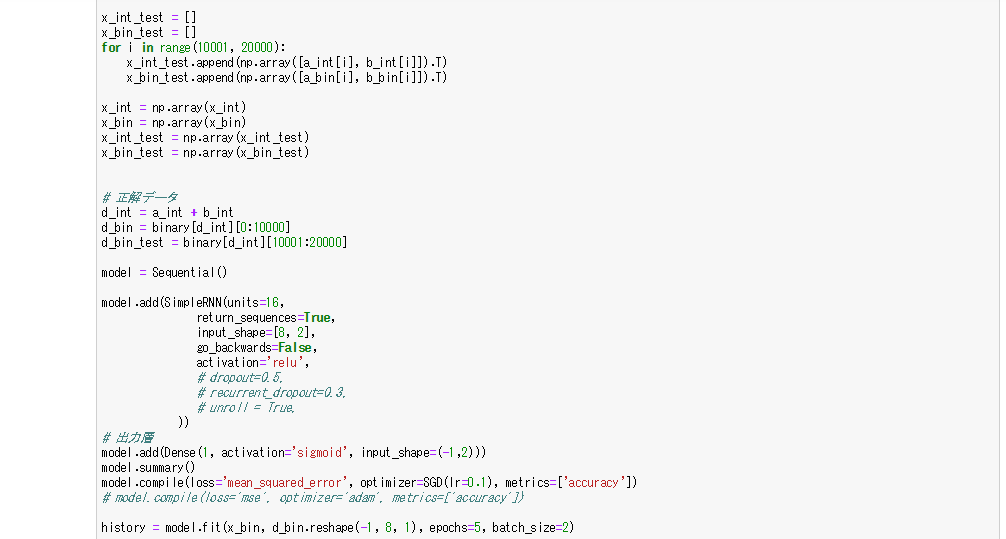
RNN
- 2進数の計算を行うRNN
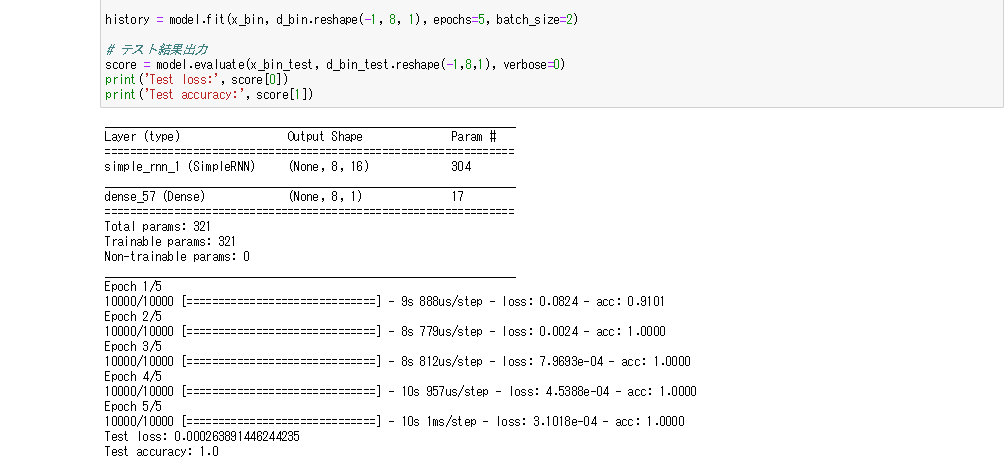
- 活性化関数はシグモイド関数で、誤差関数は平均二乗誤差、オプティマイザーはSGDを使用
- RNNのノード数を128に変更しても、学習の精度は変わらず100%のままだった
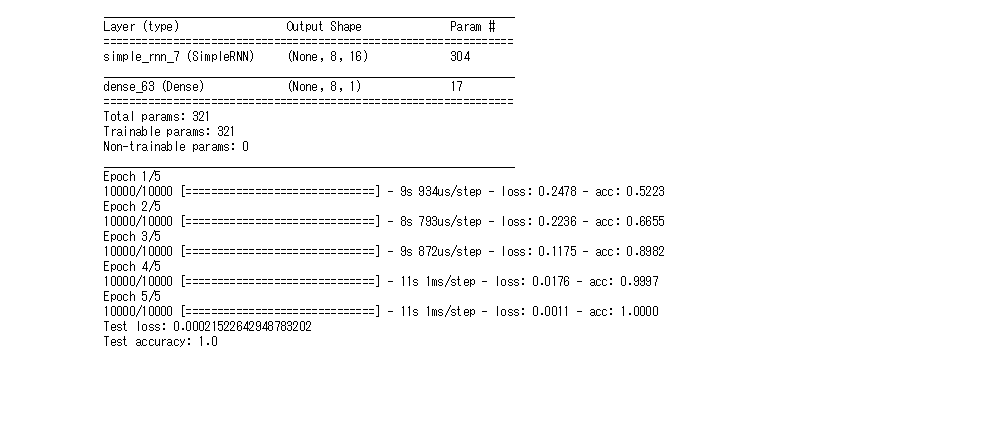
- 活性化関数をrelu関数にした場合、正解率が下がった
- 活性化関数をtanh関数にした場合、シグモイド関数同等の結果を得ることができた
- オプティマイザーをAdamにすると、学習の進みは遅いが最終的には初期と同様の結果を得られた
- 入力のドロップアウト率を0.5にすると、初期よりも学習精度が下がった
- 再帰のドロップアウト率を0.3にすると入力のドロップアウト率を0.5にした時よりは良いが、初期よりは学習精度が下がった
- kerasではunrollを使ってRNNを展開することで計算速度を早くすることができる。しかし、メモリを使うためデータサイズが大きい場合は有効でない
- kerasではsimpleRNNの部分をLSTMやGRUに変えることで簡単に実装することができる。そのためモデルの比較が容易である。
強化学習
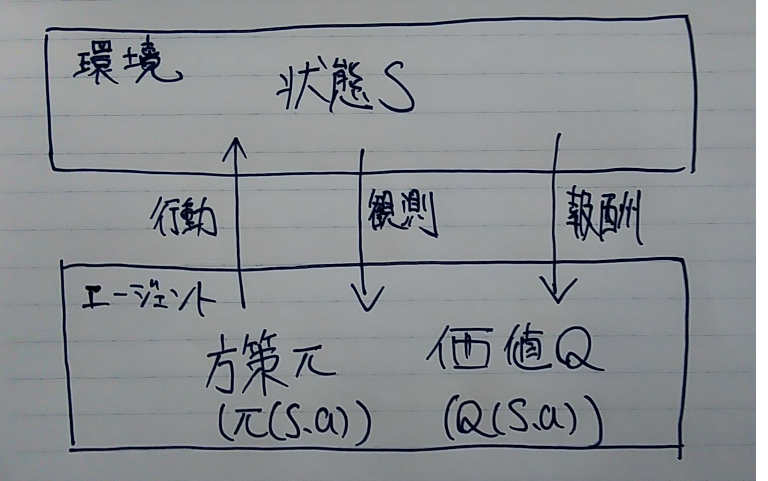
- 強化学とは長期的に報酬を最大化することを目的として、環境の中でみずから行動を選択できるエージェントを作ることを目的とした機械学習の一分野
- 報酬を最大化するための行動原理を改善する仕組み
- 例)マーケティング
- 環境：会社のマーケティング担当部署
- エージェント：顧客のプロフィールと購入履歴をもとに、キャンペーンメールを送る顧客を決めるソフトウェア
- 行動：顧客ごとにメールの送信、非送信の2つのどちらかを選択
- 報酬：メール送信のコストという負の報酬とキャンペーンで生み出される売り上げという正の報酬
- ほかにも囲碁や将棋などのゲームの分野でも利用されている
探索と利用のトレードオフ
- 環境について、「どの行動を起こせばどれくらい報酬が増える」ということを知っている場合は最適な行動をとることが可能となる
- 強化学習では上記の仮定は成り立たないとする。つまり手元にあるデータが不完全であり、新たにデータを収集しながら最適な行動を探していく
- この場合、過去のデータをもとにした最適な行動をとると未知の最適な行動を探索することができない。また、未知の行動をとり続けると過去のデータを利用することができない、というトレードオフの関係となる
強化学習のイメージ
強化学習とその他の機械学習の違い
- 教師なし学習、教師あり学習は学習データに含まれるパターンを見つけ、そのパターンをもとに未知のデータについて予測することが目標
- 強化学習は与えられた環境のなかで報酬を最大化するための行動を探すことが目標
強化学習の歴史
- 強化学習には計算速度の問題で冬の時代があった。しかし、近年CPUやGPUの高性能化により、複雑な強化学習も可能になりつつある
- また関数近似法とQ学習を組み合わせる手法も登場した
- Q学習とは行動価値関数を行動を行うたびに更新することにより、学習精度を高める手法
- 関数近似法とは行動価値関数や方策関数を関数近似する手法。関数近似することによって、行動と行動によって得られる報酬を連続値の関数で表現することができるようになるなどの利点がある
行動価値関数とは
- 価値を表す関数には状態価値関数と行動価値関数の2種類ある
- ある状態の価値に注目した関数が状態価値関数
- ある状態の時にある行動をとった時の関数が行動価値関数
方策関数
- 方策関数とはある状態においてエージェントがどのような行動をとるかの確率を与える関数
- 方策関数によって決められた確率と行動によって得られる価値によってエージェントの行動が決定される
方策勾配法
- 方策勾配法とは方策関数を最適化する手法である
- Jは方策の最適さを表し、あらかじめ定義する必要がある。その方法として平均報酬と割引報酬和の2つがある
- 平均報酬とは各行動をとったときに生まれる報酬の平均をとったもの。割引報酬和は報酬を加算する割合を徐々に減らしていったものである
- この2つに従って行動価値関数の定義をすると以下の方策勾配定理というものが成り立つ
- 方策勾配定理は状態価値関数とベルマン方程式から対数微分法を利用することで導出することができる
