【001_フィボナッチ数列】コマ大数学科
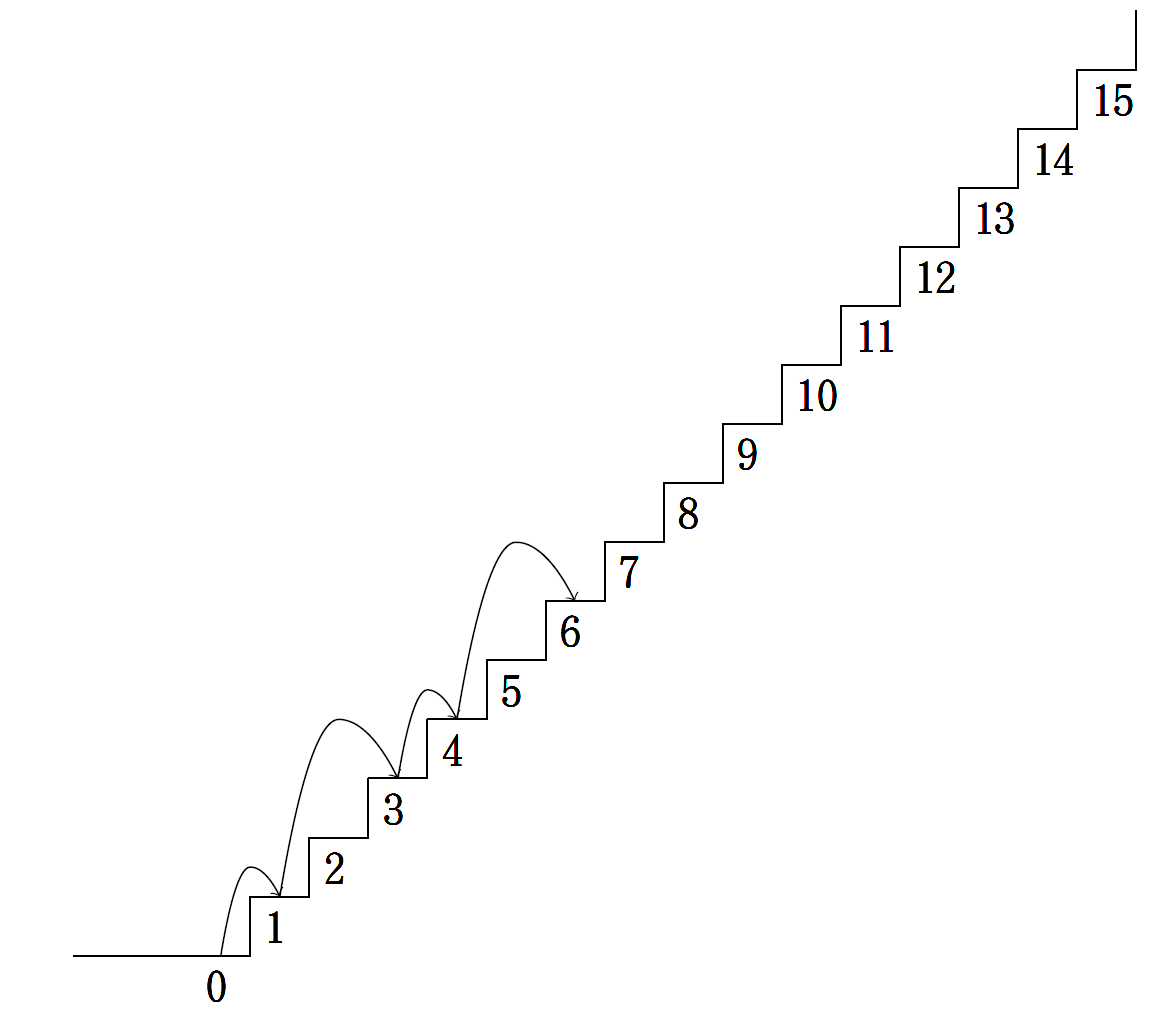
15段の階段がある。階段を上がるのには1段ずつ上がるのと2段ずつ上がるのと2通りの上がり方がある。この上がり方を組み合わせてちょうど15段上がるのは通りの登り方があるか。
\begin{tikzpicture}
% ==階段,放物線,
% 線を引く
\draw (-1,0)--(0,0);
\draw (-1,0)--(0,0);
\foreach \x in {0,0.5,1,...,7.5}
\foreach \y in {0,1,2,...,15}
{
\draw ({\x},{\x})-|({(\x)+(0.5)},{(\x)+(0.5)});
\coordinate (\y) at ({\y/2+0.25},{\y/2});
\node at ({\y/2},{\y/2})[below right]{\y};
}
\draw [->](0) parabola bend ($(0)+(0.25,0.75)$) (1); % 1段飛ばし
\draw [->](1) parabola bend ($(1)+(0.5,1.5)$)(3); % 2段飛ばし
\draw [->](3) parabola bend ($(3)+(0.25,0.75)$) (4); % 1段飛ばし
\draw [->](4) parabola bend ($(4)+(0.5,1.5)$)(6); % 2段飛ばし
\end{tikzpicture}