はじめに
MNISTのデータセットを、softmax関数と交差エントロピーなどを使って、学習させるチュートリアルをやった人に向けてですね。
そこでブラックボックスになってた softmax関数、交差エントロピー、最急降下法の解説です。
MNISTチュートリアル
tensorflowの公式チュートリアルとしてあったのだが、最近なくなったようです。
エキスパート編しか残ってませんでした。
https://www.tensorflow.org/tutorials/layers
この人が詳しく解説(日本語訳)してくれているので、概要や実装に関してはノータッチで行きます。
https://qiita.com/uramonk/items/c207c948ccb6cd0a1346
モデルはこのようなものです。(画像拝借元URLがなくなった?)
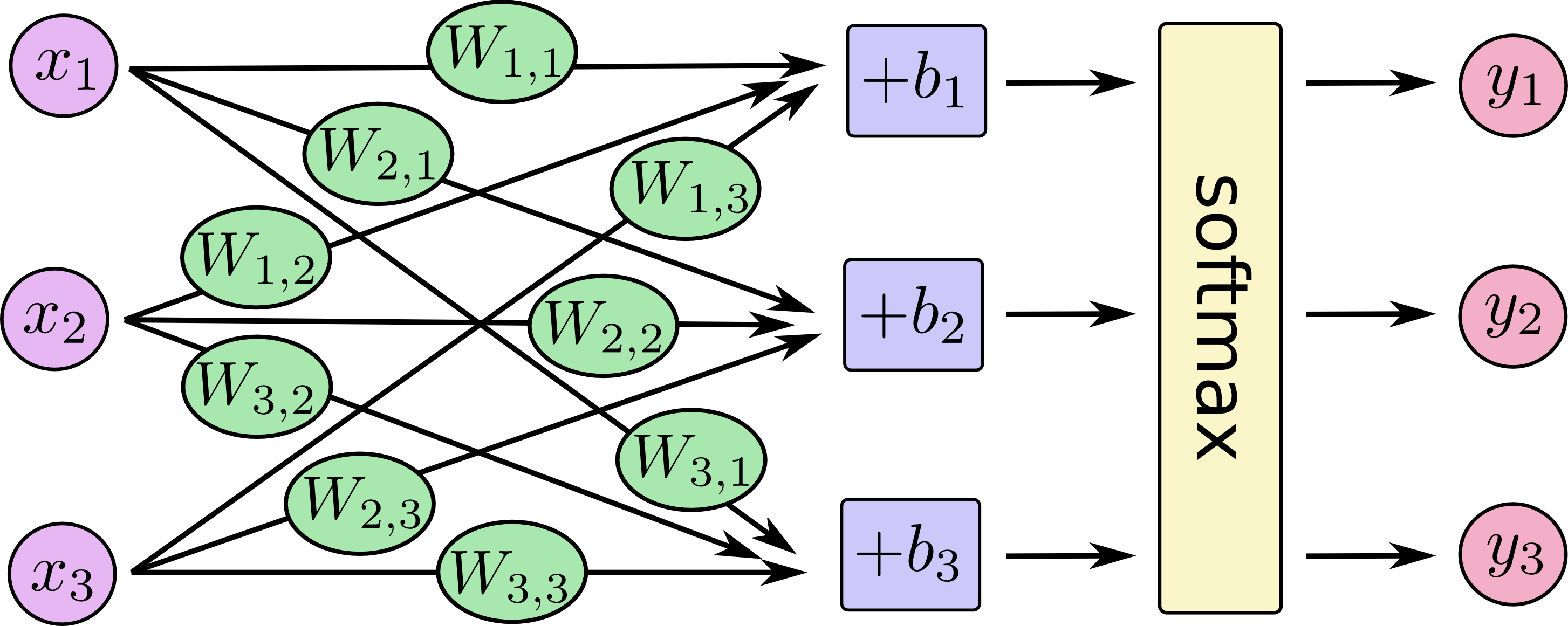
数式にしてみましょう。$n=28^2$、$m=10$として、($x$と$w$が逆だが視覚的にこの順にした)まず、softmaxに入れる前の計算をします。
\begin{pmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n \\
\end{pmatrix}
\cdot
\begin{pmatrix}
w_{11} & w_{12} & \cdots & w_{1n} \\
w_{21} \\
\vdots \\
w_{m1} & w_{m2} & \cdots & w_{mn} \\
\end{pmatrix}
+
\begin{pmatrix}
b_1 \\
b_2 \\
\vdots \\
b_m \\
\end{pmatrix}
=:
\begin{pmatrix}
z_1 \\
z_2 \\
\vdots \\
z_m \\
\end{pmatrix}
\mbox{つまり}, z_i = \sum_{k=1}^m w_{ik}x_k + b_i \quad (i=1, \cdots 10)
input $x$に対して$z_1$ は、画像が0である場合の数のようなもの、$z_2$ は、画像が1である場合の数のようなものです。
softmax関数
次にsoftmaxの定義をします。
z=(z_1,\cdots ,z_m )^T \mbox{に対して}, \\
f_i(z) := softmax(z)_i = \frac{e^{z_i}}{\displaystyle \sum_{k=1}^m e^{z_k}} \quad (i=1, \cdots 10)
これは、 ${z_i}$ それぞれの指数をとったものの確率になります。しかし、そもそも確率であるならば
f_i(z) = \frac{z_i}{\displaystyle \sum_{k=1}^m z_k}
でいいじゃんと思うかもしれないが、線形関数だとネットワークを多層化する意味がなくなるので、非線形関数にしてます(おいおい多層化するので)。ここら辺を参考にしてください。http://tarepan.hatenablog.com/entry/2015/10/06/183036
ということで、outputとして $y$(最初の図の一番右)をこのようにできます。
y_i= \frac{e^{z_i}}{\displaystyle \sum_{k=1}^m e^{z_k}} \quad (i=1, \cdots 10)
softmax関数を通すことで、$y_1$が、input画像が0である確率($y_i$が、input画像が(i+1)である確率)になってます。

これがちゃんと予想ができるように、訓練データたくさん学習させて$w$ と $b$ を決定していきます。
交差エントロピー
ここで、input $x$のラベルが3の時は、
y^{\prime} =(y_1,\cdots ,y_{10} )^T = (0,0,0,1,0,0,0,0,0,0)
input $x$のラベルが1の時、
y^{\prime} =(y_1,\cdots ,y_{10} )^T = (0,1,0,0,0,0,0,0,0,0)
などになるように input画像のラベル $y^{\prime}$を考えます。
ここで、誤差関数を$w,b$の関数として以下に定義します。これがcross entropyってやつです。これの最小化を考えます。
E(w,b) = -\sum_{k=1}^m y^{\prime}_k \log y_k \quad \cdots \quad (1)
素直に考えると、下のような奴(2)の最小化(実際の値と計算した値の差を最小にする)を目指せばいい気がするんですが、先人の賢い人たちが上のようなもの(1)も良いよっておっしゃってます。
E(w,b) = \sum_{k=1}^m ||y^{\prime}_k - y_k|| \quad \cdots \quad (2)
(1)の正当性を確認します。まず、シグマ和に関して。
$y^{\prime}$は和の添字$k$に関して、正解のひとつのみ1でそれ以外は0です。例えば、input画像が5の時は、$i=(5+1)$ 以外では$y_i^{\prime}=0$ なので、
E(w,b) = -\sum_{k=1}^m y^{\prime}_k \log y_k = -\log(y_{5+1})
つまり、さんざん上の方で$y$を計算しましたが、その正解の部分しか使わないよってことです。
次に、$f(\theta )=-\log(\theta)$を考えます。
この関数は、$0$付近でかなり大きい値になり、$1$で$0$になります。
また、先ほどの input画像が5を考えると、正しい訓練というのが、$y_{5+1}$が $1$ になることなので、$E(w,b) = -\log(y_{5+1})$ が最小化することと同じ意味になります。( $y_{5+1}=1$ の時、 $E(w,b) = -\log(y_{5+1}) =0$ になる)

よって、下記を求めるように$(w,b)$ を求めればいいのです。
\min_{w,b} E(w,b) =\min_{w,b}\left( -\sum_{k=1}^m y^{\prime}_k \log y \right)
最急降下法 (Gradient Descent)
これ日本語で読みづらいですよね。英語そのままでいいじゃんって思ってます。
一般的な最急降下法の解説します。$\min_{\theta} J(\theta)$ を求めるために、まず $y= J(\theta)$ とします。
・・・・・解説しようと思ったけど、僕はこれ以上噛み砕けない。
以下のように $\theta$ を更新すればいい。
\theta = \theta - \alpha \cdot \frac{\partial J(\theta)}{\partial \theta} \qquad \alpha \in \mathcal{R}
(このイコールは数学的な書き方でなく、プログラム的な書き方です。)

とういうことで、魔法の言葉
tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
で学習してくれます。
終わりに
巨人の肩に乗れとはいうものの、ハシゴでもかかってないと高すぎて登れないよね。