本稿ではpythonを使用して信頼区間から株式の平均収益を見積もる。
前回の記事と同様、今回もトヨタ自動車(7203)を対象に分析を行う。
# 使用するモジュールのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
import datetime as dt
import pandas_datareader.data as web
from scipy.stats import norm
# ticker入力 (今回はトヨタ自動車)
ticker_symbol="7203"
ticker_symbol_dr=ticker_symbol + ".JP"
# 期間の指定
start='2003-01-01'
end = dt.date.today()
# データ取得
toyota = web.DataReader(ticker_symbol_dr, data_source='stooq', start=start,end=end).sort_values("Date")
これでサンプルの用意はできたが、このサンプルが母集団の"良い代表"であれば、母集団の平均は標本平均に近くなる。少なくとも、母集団の平均は標本平均を中心としたある一定の範囲内にあると考えられる。
そのため、この分析において我々が行うべきことは、母集団の平均が位置する範囲を見積もることである。
そのためには、異なるサンプルは異なる平均と標準偏差を持つため、標本平均を標準化する必要がある。
ご案内の通り、標本平均の分布は正規分布である。標本平均を標準化するためには母集団の平均から標本平均分布の平均を引き、母集団の分散を標本サイズnの平方根で割った標本分散で除する必要がある。
\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}
標準化した後は標準正規分布となり、これはZ分布に従うようになる。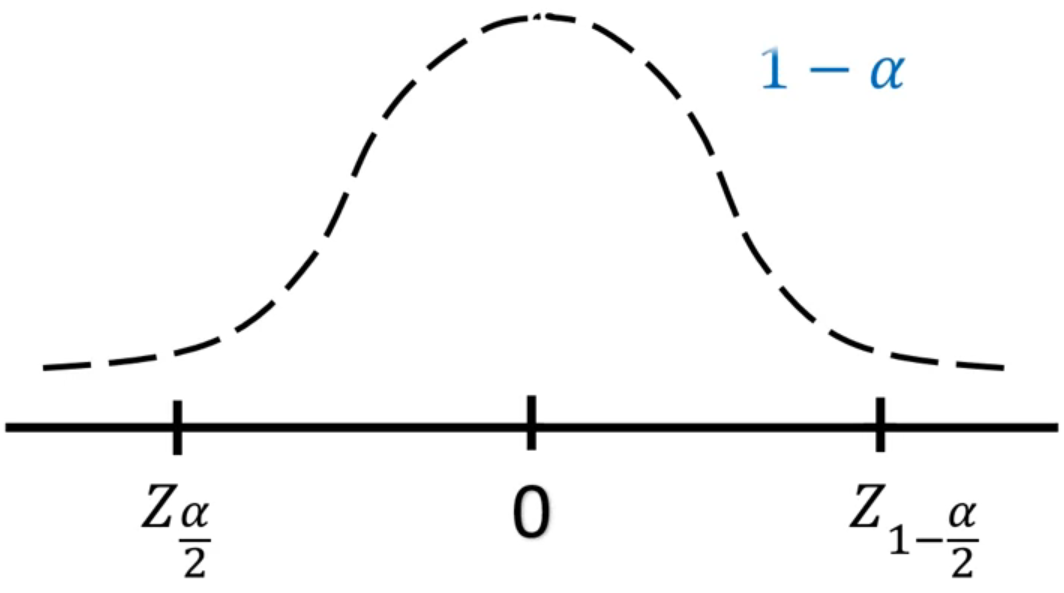
この分布における$Z_\frac{\alpha}{2}$と$Z_{1-\frac{\alpha}{2}}$の間の確率は$1-\alpha$となる。Z分布は0を中心に左右対称となるので、$-Z_\frac{\alpha}{2} = Z_{1-\frac{\alpha}{2}}$となる。
標本平均の標準化した形もZ分布であるため、
P(Z_\frac{\alpha}{2} \leq \frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}} \leq Z_{1-\frac{\alpha}{2}}) = 1 - \alpha
を得られる。これを式変形すると以下のようになる。
P(\bar{X} - \frac{\sigma}{\sqrt{n}}Z_\frac{\alpha}{2} \leq \mu \leq \bar{X} + \frac{\sigma}{\sqrt{n}}Z_\frac{\alpha}{2}) = 1-\alpha
これは、母集団平均、すなわち期待リターンの上限と下限を示してくれるものである。
この$\sigma$は母集団の標準偏差であり通常はわからない値である。しかし、実務上はサンプル数が十分に大きければ標本標準偏差に置き換えて計算してしまうことができる。
ここで、$\mu$の範囲は「$1-\alpha$のレベルの信頼区間」を呼ばれる。
それでは、実際にトヨタの平均リターンを見積もってみる。ここでの$\frac{\alpha}{2}$は0.05とした(すなわち、信頼水準は90%である)。
# Lets build 90% confidence interval for log return
sample_size = toyota['LogReturn'].shape[0]
sample_mean = toyota['LogReturn'].mean()
sample_std =toyota['LogReturn'].std(ddof=1) / sample_size**0.5
# left and right quantile
z_left = norm.ppf(0.05)
z_right = norm.ppf(0.95)
# upper and lower bound
interval_left = sample_mean + z_left * sample_std
interval_right = sample_mean + z_right * sample_std
結果として、トヨタの平均収益は90%の確率で、
(-0.00013182221183375743, 0.0006855071186437733)
に収まることが分かった。
ここでもし下限の値がプラスであれば、その銘柄は強い上昇トレンドにあるということが言えるだろう。