Pythonで株式の日次リターンの対数分布からリスクを測定する

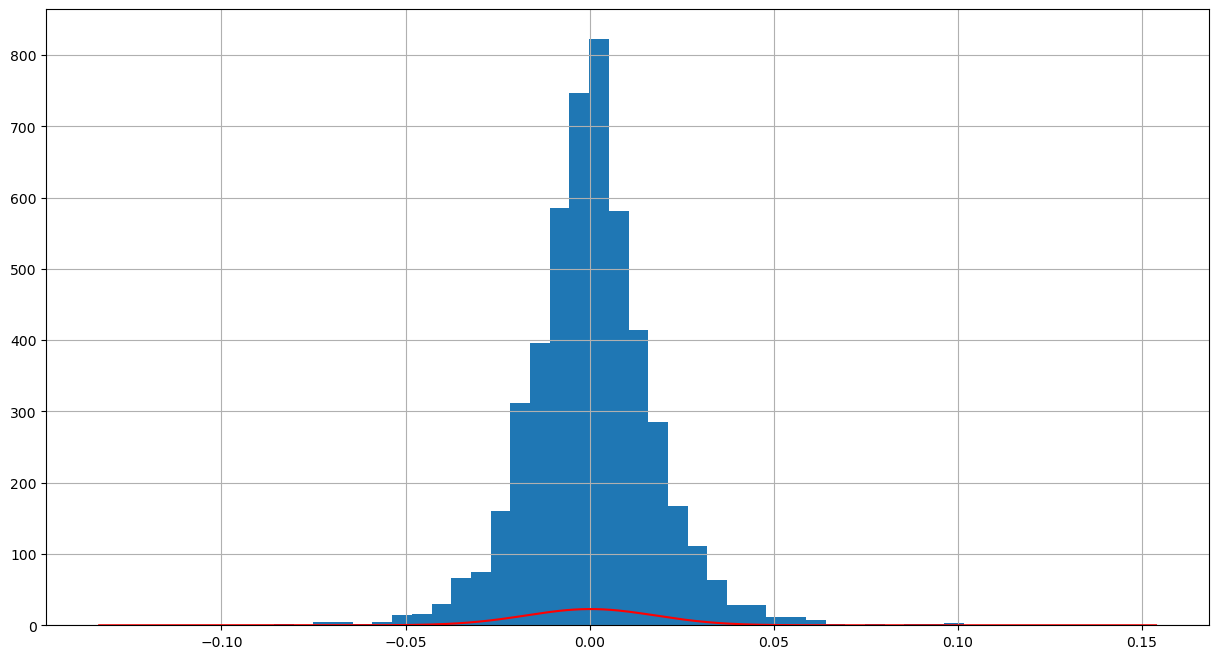
　本稿ではpythonを使用して株式の日次リターンの対数分布を見ることで、株式投資のリスクを測定してみる。

　まず、pandasの拡張モジュールであるpandas_datareaderを事前にインストールしておく。

pip install pandas_datareader

　今回は例としてトヨタ自動車を見てみる。

# 使用するモジュールのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
import datetime as dt
import pandas_datareader.data as web
from scipy.stats import norm

# ticker入力 (今回はトヨタ自動車)
ticker_symbol="7203"
ticker_symbol_dr=ticker_symbol + ".JP"
 
# 期間の指定
start='2003-01-01'
end = dt.date.today()
 
# データ取得
toyota = web.DataReader(ticker_symbol_dr, data_source='stooq', start=start,end=end).sort_values("Date")

# 最初の5行を表示
toyota.head()

これを実行すると下図のように、2003年1月以降の株価のデータを得られる。

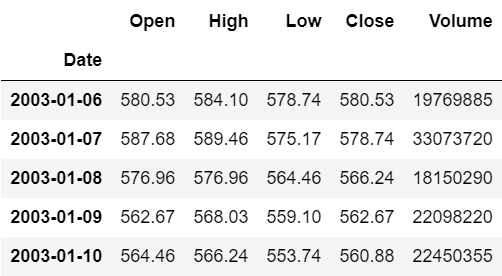
# 日時の対数リターンをとり、"LogReturn"というコラムに格納する。
toyota['LogReturn'] = np.log(toyota['Close']).shift(-1) - np.log(toyota['Close'])

# 対数リターンの平均と標準偏差を計算
mu = toyota["LogReturn"].mean()
sigma = toyota["LogReturn"].std(ddof=1)

# 確率密度関数を計算
density = pd.DataFrame()
density["x"] = np.arange(toyota["LogReturn"].min()-0.01, toyota["LogReturn"].max()+0.01, 0.001)
density["pdf"] = norm.pdf(density["x"], mu, sigma)

# 結果をプロット
toyota["LogReturn"].hist(bins=50, figsize=(15, 8))
plt.plot(density["x"], density["pdf"], color="red")
plt.show()

　FamaとFrenchは株式の収益率は正規分布よりも裾が厚くなると述べているが、トヨタの場合はだいぶ裾が薄い。仮説的に大企業であればあるほど、そしてバリュー株であればあるほど裾は薄くなる気がする。

　以下のコードではトヨタが1日で5%以上、10%以上下落する確率を計算する。

# 1日で5%以上下落する確率を計算
prob_return_5per = norm.cdf(-0.05, mu, sigma)*100
# 1日で10%以上下落する確率を計算
prob_return_10per = norm.cdf(-0.1, mu, sigma)*100
print(prob_return_5per, "%")
print(prob_return_10per, "%")

　これらを実行すると、それぞれ「0.2095516733415158 %」、「5.537040982959987e-07 %」を得られる。

　また、以下では1年間で40%以上、ないしは20%以上下落するリスクを計算する。ここでは1年間の東証が開いている日数を245日で計算した。

mu245 = 245*mu
sigma245 = (245**0.5) * sigma

# 245日で40%以上下落する確率
print(norm.cdf(-0.4, mu245, sigma245) * 100, "%")

# 245日で20%以上下落する確率
print(norm.cdf(-0.2, mu245, sigma245) * 100, "%")

　このコードを実行すると、それぞれ「4.777794106749807 %」、「17.40000427850144 %」が得られた。

　次にValue at Risk (VaR)を計算してみる。「XX％ Value at Risk」の概念は、ある投資について一定の期間かつ一定の信頼度(XX％)で予想される損失の最大額を測定するものである。これは「あらかじめ定義された信頼度において、ある時間軸で失われると予想される最大の金額」と定義される。例えば、95％ VaRは、潜在的な損失の分布の95パーセンタイルとなる。VaRは、投資のリスクを測定する方法であり、どれだけの損失を被る可能性があるか、その可能性はどの程度か、どのような時間軸で損失が発生するかという問いに答えるものである。

# 95% Value at Riskの計算
VaR = norm.ppf(0.05, mu, sigma)

　これを実行すると「-0.02862165919988984」が得られる。これは「1日で2.86%以上の損失を被る可能性は5%以下である」と解釈できる。