この記事は「数理最適化 Advent Calendar 2020」22日目の記事です。
21日目は@shuhei_fさんによる「SMOのworking setの選び方」でした。
はじめに
Pythonと最適化モデリングライブラリGoogle OR-Toolsを用いて、簡単な最適化プロジェクトを進めていきます。題材は「個別指導塾における講師のシフト作成」で、0-1整数線形計画問題として解きます。
プログラムを書くのがド下手なので、「こう書いた方がいい」といったことは是非教えてください。
問題発生
渋川君のアルバイト先の個別指導塾では、以下のようなシフト表に基づいて勤務することになっています。
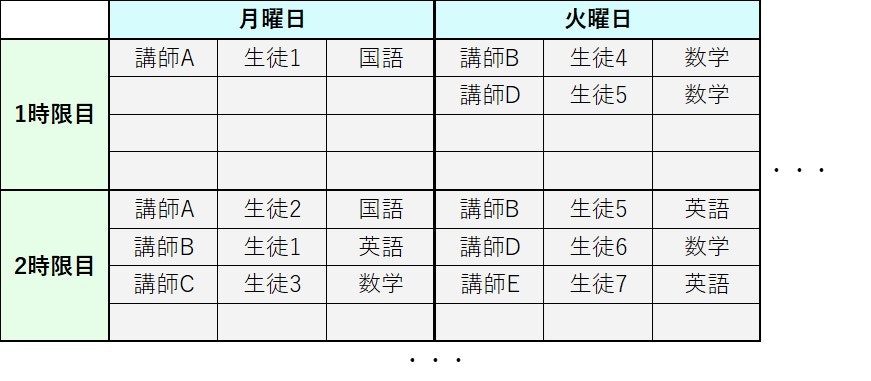
例えば月曜1限では、講師Aが生徒1に対して国語を教えることになっています。
シフト表は一か月間固定で、毎月20日に教室長が翌月分のシフト表を作成します。
今の教室長は非常に雑な人で、
・数学を担当できない講師が数学を教えることになっている
・希望を出していない曜日にシフトが入れられている
といったことが多発しています(※これはフィクションです)。
そこで最近最適化に興味を持ち始めた読んだ渋川君が、数理最適化を使ってシフト表を自動生成してみようと考えました。
どうしたいのかを考える
ざっくりと「シフトを自動生成したい」と述べましたが、もう少し具体的に、最適化でどうなって欲しいかを考えてみます。
今回の例では、教室長が作るシフトが条件を満たしてさえいなかったので、一旦は条件を満たすような解を見つけるだけでも十分な気がします。実行可能解がないにしても、満たせない条件をなるべく少なくするようにモデリングすれば調整が楽そうです。
したがって、まずは条件を満たす解を見つけることから始め、それが出来たら何を最大化または最小化したいか考えることにします。
どんな問題に落とし込むかを考える
長い前置き
早速定式化に取りかかります。定式化とは、「決定変数、制約条件、目的関数を数式で表すこと」であると認識しています。 個人的には、定式化の最初のステップとして「どんな問題になりそうか」を考える必要があると思っています。例えば「どんな順番にすると一番良いか知りたいから巡回セールスマン問題かな?」って感じです。 実務では多くが組合せ最適化問題に帰着することが多く、組合せ最適化問題には典型問題と呼ばれるものが存在します(巡回セールスマン問題も典型問題の一つ)。典型問題を知っていると定式化がしやすいですし、効率的な解法が盛んに研究されているので参考になります。そのため典型問題にどんなものがあるか、どんな応用例があるか知っておくと良いのかなと思います(これは自分への戒めでもあります)。 典型問題は、[斉藤先生のこちらの記事] (https://qiita.com/SaitoTsutomu/items/0f6c1a4415d196e64314)や[NTTデータ数理システムのこちらのサイト](https://www.msi.co.jp/nuopt/docs/v22/examples/html/01-00-00.html)に良くまとまっています。今回のプロジェクトでは「どの講師が、どの曜日・時限・科目に割り当てられるか」を決めると良さそうなので、割当問題が使えそうです。
※実際は「どの生徒に割り当てられるか」ですが、今回は簡単のために「ある生徒に割り当てられる=その生徒が受講を希望する科目に割り当てられる」と考えます。同じ科目の受講を希望する生徒が複数いる場合はどっちを担当してもよいものとします。
割当問題は適用できるシーンが非常に多く、定式化も分かりやすいので、とにかく何か最適化してみたい時の入り口としてかなりおすすめです。
決定変数を考える
ここからは数式による表現とPythonによる実装を並行して進めていきます。実装に関しては記事の流れの都合上変数の登場順序などが前後して分かりづらいですがご容赦ください。
決定変数は雑に言うと「コレが分かったら嬉しいモノ」です。巡回セールスマン問題でいえば「訪問順序」が決定変数で、「総移動距離(最小にしたい)」が目的関数です。決定変数をどう設定するかで目的関数や制約式の作りやすさが変わるので重要なのですが、このプロジェクトではゴリ押しでいきます。
数式
今回は上述のように「どの講師が、どの曜日のどの時限にどの科目を担当するか」を決めたいので、これをそのまま変数にします。
講師$i$が曜日$w$の時限$t$に科目$s$を担当するかどうかを表す変数を以下のように表します。
x^i_{wts} \in \{0,1\}
$x^i_{wts} =1$であれば、担当する(=シフトが入る)という意味になります。
実装
最初にpywraplp.Solver(問題名,使用するソルバー)でソルバーを宣言します。今回は無料で使える混合整数計画ソルバーCBCを指定します。そしてsolver.IntVar(下限,上限,変数名)で整数変数を作成します。
from ortools.linear_solver import pywraplp
# 曜日・時限・科目のリスト
weekday_list = ['月','火','水','木','金','土']
timetable_list = [1,2,3,4]
subject_list = ['国語','数学','英語']
# 講師数、曜日数、時限数、科目数
I,W,T,S = len(shift_avlbl),len(weekday_list),len(timetable_list),len(subject_list)
# ソルバーの宣言
solver = pywraplp.Solver('Staff Scheduling',pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)
# 決定変数x
x = [[[[solver.IntVar(0,1,'') for s in range(S)] for t in range(T)] for w in range(W)] for i in range(I)]
x[i][w][t][s]が上述の$x^i_{wts}$を表します。
制約式を考える
今の教室長が守ってくれてないやつです。
シフトに関して満たさなければならない条件ですが、ぱっと思いつく範囲では
・一人の講師が担当するのは生徒一人まで
・希望していない日時にシフトを入れない
・(得意不得意の理由で)担当できない科目のシフトを入れない
・過不足なくシフトを入れる
あたりになりそうです。今回はあくまで講師に優しくというスタンスでいきます。
この他に
・生徒側(講師側)から共演NGが出ている講師(生徒)
・中学受験経験者の講師を希望する生徒
などがありましたが、今回は考慮しないことにします。
とりあえず最初に述べた4つを制約としたいと思います。
一人の講師が担当するのは生徒一人まで
私が所属していた塾では講師:生徒=1:2での授業でしたが、今回は簡単のためマンツーマンにします。
数式
次のような数式を考えます。
\sum_s x^i_{wts} \leq 1 \quad \forall i,w,t
実装
solver.Add(等式制約または不等式制約)で制約式を作成します。
また、solver.Sum()で通常のsum()より速く計算することが出来ます。
# 制約 一人の講師が担当できる生徒は一人まで
for i in range(I):
for w in range(W):
for t in range(T):
solver.Add(solver.Sum([x[i][w][t][s] for s in range(S)]) <= 1)
希望していない日時にシフトを入れない
講師からは、以下のようなシフト希望表を受け取っているものとします。
今回は板垣先生作「グラップラー刃牙」より、7名の方に講師を担当して頂いています。

数式
次のように、希望しない日時に関しては最初から0になるように制約式を考えます。
\sum_s x^i_{wts} = 0 \quad \forall i,w,t \in講師iが希望しない日時
実装
shift_avlblに上のシフト希望表がpandasのDataFrameとして格納されているものとします。
曜日・時限が横一列に並んだ状態から曜日インデックスと時限インデックスを取得するために、4で割った商と余りを用いています(今回は各曜日4限まであるため)。
# 制約 希望しない日時にシフトを入れない
for i in range(I):
for j in range(len(shift_avlbl.columns)):
#この日時を希望しなければ
if shift_avlbl.iat[i,j] == 0:
unavlbl_w = j//4 #曜日インデックス
unavlbl_t = j%4 #時限インデックス
solver.Add(solver.Sum([x[i][unavlbl_w][unavlbl_t][s] for s in range(S)]) == 0)
担当出来ない科目のシフトを入れない
シフト希望表と同様に、講師から次のような担当可能科目の情報を受け取っているものとします。
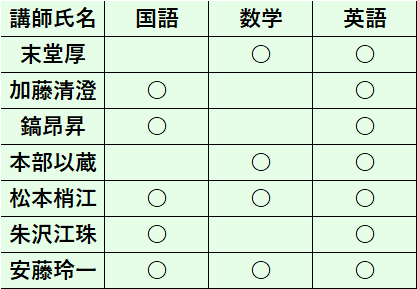
数式
先ほどと同様に、担当できない科目には最初から割り当ての可能性をなくすという形をとります。
\sum_{w,t} x^i_{wts} = 0 \quad \forall i,s \in講師iが担当できない科目
実装
subject_avlblに上の担当可能科目の情報がpandasのDataFrameとして格納されているものとします。
# 制約 担当できない科目のシフトをいれない
for i in range(I):
for s in range(S):
if subject_avlbl.iat[i,s] == 0:
solver.Add(solver.Sum([x[i][w][t][s] for w in range(W) for t in range(T)]) == 0)
過不足なくシフトを入れる
以下のような表で受講管理を行っているとします。
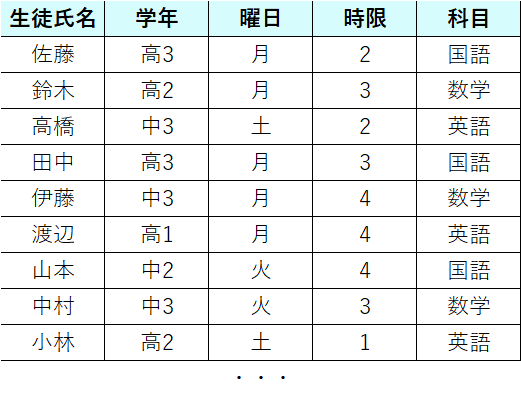
画像は途中までになっていますが、41件の登録があります。
数式
この表によって、「どの日時にどの科目が何人分需要されているか」が分かるので、曜日$w$の時限$t$における科目$s$の需要量として$D_{wts}$という定数を考えます。
そして、過不足なくシフトを入れることは需要を丁度満たすことと考えられるので、以下の制約式を考えます。
\sum_i x^i_{wts} = D_{wts} \quad \forall w,t,s
まずは条件を全て満たすシフトを決めることが最初の目的でしたが、これまでに登場した制約を考えると、「実行可能解がない」可能性が十分にあります。実行可能解がないとソルバーの出力としての解は得られなくなってしまうので、対策として上記の制約式を緩めます。
新たな決定変数$y_{wts}$を用いて、以下の制約式に変更します。
\sum_i x^i_{wts} + y_{wts} = D_{wts} \quad \forall w,t,s
$y_{wts}$は、「曜日$w$の時限$t$における、科目$s$を担当する講師の不足分」と解釈出来ます。そして、目的関数として
min \quad \sum_{w,t,s} y_{wts}
を考えれば、「講師不足数」を最小化する問題となり、目的関数値が0であれば全ての制約を守れていることになります。また、0じゃなくても、最適解$y$の中身を参照することで「何曜日の何限に何の科目の講師が何人足りないのか」が分かるため、講師間での調整が出来ます。
実装
lecture_reqに先ほどの受講管理票がDataFrameで格納されているものとし、$D_{wts}$を表す配列demandを作成します。決定変数$y_{wts}$は事前に作成してあるものとして、以下のコードで制約式を加えます。
# 各曜日・各時限における各科目の需要量を表す配列
demand = [[[0 for s in range(S)] for t in range(T)] for w in range(W)]
for index,row in lecture_req.iterrows():
weekday = weekday_list.index(row['曜日'])
timetable = timetable_list.index(row['時限'])
subject = subject_list.index(row['科目'])
demand[weekday][timetable][subject] += 1
# 制約 過不足なくシフトを入れる
for w in range(W):
for t in range(T):
for s in range(S):
solver.Add(solver.Sum([x[i][w][t][s] for i in range(I)]) + y[w][t][s] == demand[w][t][s])
目的関数を考える
上述の通り、最初は「講師不足数の総和」を目的関数として最小化することで、実行可能解があるかどうかを確認し、なければ講師のシフト希望を調整します。実行可能解がある状態にできたら、最適なシフトを目指して別の目的関数を考えることにします。
数式
最初の目的関数を再掲します。
min \quad \sum_{w,t,s} y_{wts}
実装
solver.Minimize(目的関数)で目的関数を作成します。最大化問題のときはsolver.Maximize(目的関数)とします。
また、solver.Solve()で最適化計算が行われ、返り値としてソルバーのステータスが得られます。ステータスが0であれば最適解が求まったことになります。
# 講師不足数の総和
shortage = solver.Sum([y[w][t][s] for s in range(S) for t in range(T) for w in range(W)])
# 目的関数の設定
solver.Minimize(shortage)
# 求解
status = solver.Solve()
全体のコード
データを取得してから、シフトを出力するまでの一連のコードを記載します。
import pandas as pd
from ortools.linear_solver import pywraplp
"""必要なデータ"""
# シフト希望表
shift_avlbl = pd.read_excel('~/data.xlsx',sheet_name='シフト希望表').set_index('講師氏名').applymap(lambda x: 1 if x=='〇' else 0)
# 担当可能科目
subject_avlbl = pd.read_excel('~/data.xlsx',sheet_name='担当可能科目').set_index('講師氏名').applymap(lambda x: 1 if x=='〇' else 0)
# 受講管理表
lecture_req = pd.read_excel('~/data.xlsx',sheet_name='受講管理表')
"""最適化"""
# 曜日・時限・科目のリスト
weekday_list = ['月','火','水','木','金','土']
timetable_list = [1,2,3,4]
subject_list = ['国語','数学','英語']
# 講師数、曜日数、時限数、科目数
I,W,T,S = len(shift_avlbl),len(weekday_list),len(timetable_list),len(subject_list)
# ソルバーの宣言
solver = pywraplp.Solver('Staff Scheduling',pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)
# 決定変数x
x = [[[[solver.IntVar(0,1,'') for s in range(S)] for t in range(T)] for w in range(W)] for i in range(I)]
# 決定変数 y
y = [[[solver.IntVar(0,4,'') for s in range(S)] for t in range(T)] for w in range(W)]
# 制約 一人の講師が担当できる生徒は一人まで
for i in range(I):
for w in range(W):
for t in range(T):
solver.Add(solver.Sum([x[i][w][t][s] for s in range(S)]) <= 1)
# 制約 希望しない日時にシフトを入れない
for i in range(I):
for j in range(len(shift_avlbl.columns)):
if shift_avlbl.iat[i,j] == 0:
unavlbl_w = j//4 #曜日インデックス
unavlbl_t = j%4 #時限インデックス
solver.Add(solver.Sum([x[i][unavlbl_w][unavlbl_t][s] for s in range(S)]) == 0)
# 制約 担当できない科目のシフトをいれない
for i in range(I):
for s in range(S):
if subject_avlbl.iat[i,s] == 0:
solver.Add(solver.Sum([x[i][w][t][s] for w in range(W) for t in range(T)]) == 0)
# 各曜日・各時限における各科目の需要量を表す配列
demand = [[[0 for s in range(S)] for t in range(T)] for w in range(W)]
for index,row in lecture_req.iterrows():
weekday = weekday_list.index(row['曜日'])
timetable = timetable_list.index(row['時限'])
subject = subject_list.index(row['科目'])
demand[weekday][timetable][subject] += 1
# 制約 過不足なくシフトを入れる
for w in range(W):
for t in range(T):
for s in range(S):
solver.Add(solver.Sum([x[i][w][t][s] for i in range(I)]) + y[w][t][s] == demand[w][t][s])
# 講師不足数の総和
shortage = solver.Sum([y[w][t][s] for s in range(S) for t in range(T) for w in range(W)])
# 目的関数の設定
solver.Minimize(shortage)
# 求解
status = solver.Solve()
"""結果の表示"""
print('ステータス:',status)
print('講師不足数:',solver.Objective().Value())
# 最適解
x_solution = [[[[int(x[i][w][t][s].SolutionValue()) for s in range(S)] for t in range(T)] for w in range(W)] for i in range(I)]
# シフトを表すデータフレーム
teacher_list = shift_avlbl.index.tolist()
shift_df = pd.DataFrame(columns=['講師氏名','曜日','時限','科目'])
for i in range(I):
for w in range(W):
for t in range(T):
for s in range(S):
if x_solution[i][w][t][s] == 1:
shift_df = shift_df.append({'講師氏名':teacher_list[i],'曜日':weekday_list[w],'時限':timetable_list[t],'科目':subject_list[s]},ignore_index=True)
print(shift_df)
結果
上記のコードを実行した結果、以下の出力が得られました。ステータスが0なので最適解が求まっていることが分かり、目的関数である講師不足数が0なので、現状のシフト希望と受講管理表のデータでも全ての制約を満たす解が存在することが分かりました。
シフトを表すデータフレームは途中で切れていますが、受講希望数と同じ41件のシフトが出力されています。
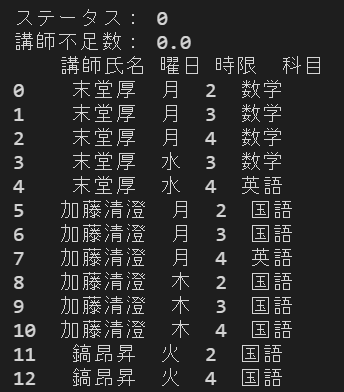
そして作成した担当表が以下になります。
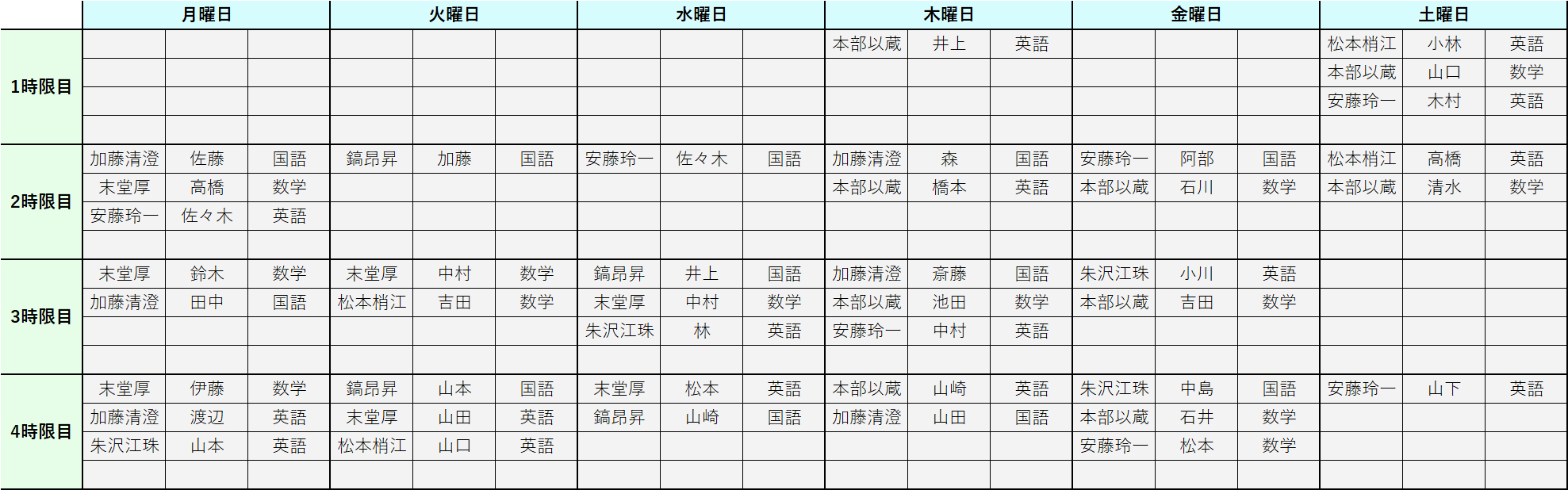
人選が適当すぎて「〇曜△限であの戦いが起こりそう」とかはありませんでした。
挫折
本当はここから別の目的関数や制約を取り入れて、より良いシフトを作る展開にしたかったのですが、上手く出来ませんでした。
取り入れたかったものとしては、「なるべく同じ日に連続でシフトに入りたい」を考えていました。朱沢先生や安藤先生のシフトを見てみると、一日に一コマだけシフトが入っていたり、空きコマがあったりします。人によるとは思いますが、なるべく一日に一気にシフトを入れることを好む方は多いと思うので、空きコマの数を最小化したり、同じシフト数でも出勤する日数を最小化するようなモデルを作りたいと考えていました。
しかしながら、私の力では整数線形計画問題になるようにこれらをモデルに取り入れることが出来ませんでした。もし整数線形計画問題になるように取り入れるアイデアや、全く異なる定式化で実現するアイデアがあったら是非お教えいただければと思います。
まとめ
達人である渋川先生にプロジェクトを失敗させてしまい申し訳ないです。そして渋川先生のシフトを完全に忘れていました。
未熟ながらアドベントカレンダーに初挑戦させて頂きましたが、悔しい部分が多いので来年また挑戦させてください。読んで頂きありがとうございました。