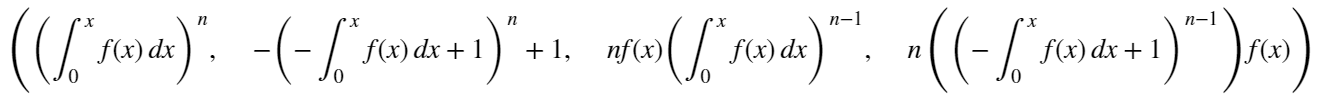統計学入門7.8をPythonで解く

#概要
以下の統計学入門の問題をPythonで解く。

#環境
Jupyter notebook

#実装

# %%
# 東京大学出版会「統計学入門」練習問題7.8のPythonによる計算。
# f_xの定義において、コメントアウトする行を変更することで、i～iiiのそれぞれに対応可能。

# ====setup
import sympy as sym
from sympy.plotting import plot
import matplotlib.pyplot as plt

sym.init_printing()
plt.rcParams["font.size"] = 13


n = sym.Symbol("n", real=True)
x = sym.Symbol("x", real=True)
oo = sym.oo
e = sym.exp(1)
lamda = sym.Symbol("lamda", real=True)


# ===ここf_xの定義

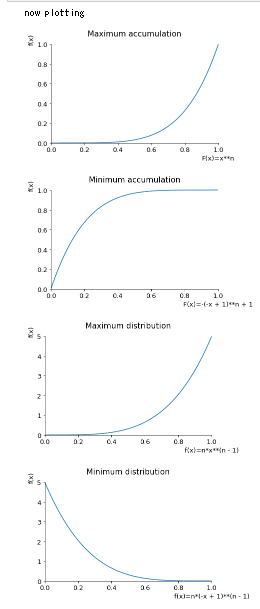
f_x=1 # i)
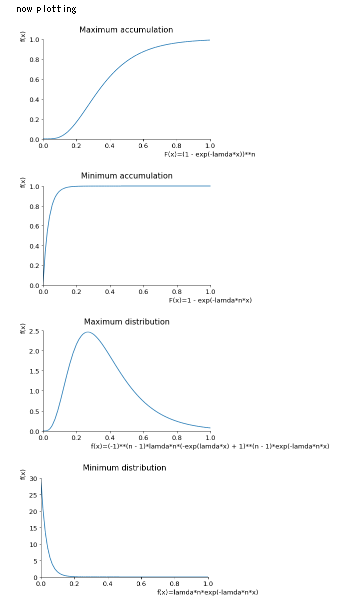
# f_x = lamda*e**(-lamda*x) # ii)
# f_x=sym.Function("f")(x) # iii)

# ===Parameters only for Plotting

lam = 6
n_v = 5
up=1

# ===integrate to know the probability which x gets 0-to-x in

p_a = sym.integrate(f_x, (x, 0, x))

# ===gets cumulative distribution function 

f_ac_max = ((p_a)**n).simplify()
f_ac_min = (1-(1-p_a)**n).simplify()

# ===gets distribution function by differential

f_max = sym.diff(f_ac_max, x).simplify()
f_min = sym.diff(f_ac_min, x).simplify()

# ===Plot

if f_x!=sym.Function("f")(x):
    print("now plotting")
    plot(f_ac_max.subs(n, n_v).subs(lamda, lam), (x, 0, up), title="Maximum accumulation",xlabel="F(x)="+str(f_ac_max))

    plot( f_ac_min.subs(
        n, n_v).subs(lamda, lam), (x, 0, up), title="Minimum accumulation",xlabel="F(x)="+str(f_ac_min))

    plot(f_max.subs(n, n_v).subs(lamda, lam), (x, 0, up), title="Maximum distribution",xlabel="f(x)="+str(f_max))

    plot( f_min.subs(n, n_v).subs(lamda, lam), (x, 0, up), title="Minimum distribution",xlabel="f(x)="+str(f_min))
    plt.show()
else:
	print(f_ac_max,f_ac_min,f_max.doit(),f_min.doit())

#結果

解答のグラフはn=5のもの。(ii)についてはλ=6と置いて図示した。
直接の答えは各グラフの右下に付記している。

(i)の解答

(ii)の解答

(iii)の解答

(iii)のグラフィカル表示