はじめに
ビュフォンの針という数学上の確率に関する問題があります。
ビュフォンの針(ビュフォンのはり、英: Buffon's needle problem)は18世紀の博物学者ジョルジュ=ルイ・ルクレール、コント・ド・ビュフォンが提起した数学上の問題である。
もし床に多数の平行線を引き、そこに針を落すならば、どれかの線と針が交差する確率はどのようになるかという問題である。
こちらの問題の詳細については、下記のサイト様でわかりやすく丁寧に解説されているので、ここでは詳しく書きませんが、
とにかく、針が線と交差する確率Pは下記になるそうです。
P = 1/π
なんと確率に円周率πが出てくるんですね、びっくり。
でもなんとなく信じがたいので、pythonでコード書いて確認してみました。
★ビュフォンの針の詳しい解説をしてくださっているサイト様★
高校数学の美しい物語
実装
とりあえず、上記のサイト様の解説の通り、
平行線の幅をd / 針の長さをl= d/2
として針をばらまくコードを書いてみます。
import tkinter as tk
import random
import math
root = tk.Tk()
root.title("buffon")
root.geometry("900x900")
## 描画領域
h = 900
w = 900
canvas = tk.Canvas(root, bg="white", height=h, width=w)
# 平行線
d = 50##平行線の幅
for j in range(h//50):
canvas.create_line(0,j*d,w,j*d)
# 針が線にかかるかの判定
def CheckLine(y_1, y_2):
if y_1 // d == y_2 // d:
return 0 ##線にかからない
else:
return 1 ##線にかかる
n = int(input("input drop needle nubmer:")) ##針の数
l = d/2 ##針の長さ 簡単のため 2l=d
line_cross = [] ##針が線にかかるかからないの結果を格納
i=0
while i < n:
x = random.uniform(d,w-d) ##針の片方の端点を落とす場所
y = random.uniform(d,h-d) ##針の片方の端点を落とす場所
theta = random.uniform(0, 2*math.pi) ##落とした針が倒れる方向
line_cross.append(CheckLine(y, y + l*math.cos(theta)))
if CheckLine(y, y + l*math.cos(theta)) == 0:
canvas.create_line(x, y, x + l*math.sin(theta), y + l*math.cos(theta))
else:#針が先にかかった場合針を赤く表示
canvas.create_line(x, y, x + l*math.sin(theta), y + l*math.cos(theta), fill = 'red')
i += 1
canvas.place(x=0, y=900-h)
m = sum(line_cross)##先にかかった針の数
print('cross line needle:' + str(m))
print('n/m :' + str(n/m))##piの近似値になるはず
root.mainloop()
とりあえず針の数を100本でやってみる。
input drop needle nubmer:100
cross line needle:28
n/m :3.5714285714285716
1,000本
input drop needle nubmer:1000
cross line needle:312
n/m :3.2051282051282053
10,000本
input drop needle nubmer:10000
cross line needle:3155
n/m :3.1695721077654517
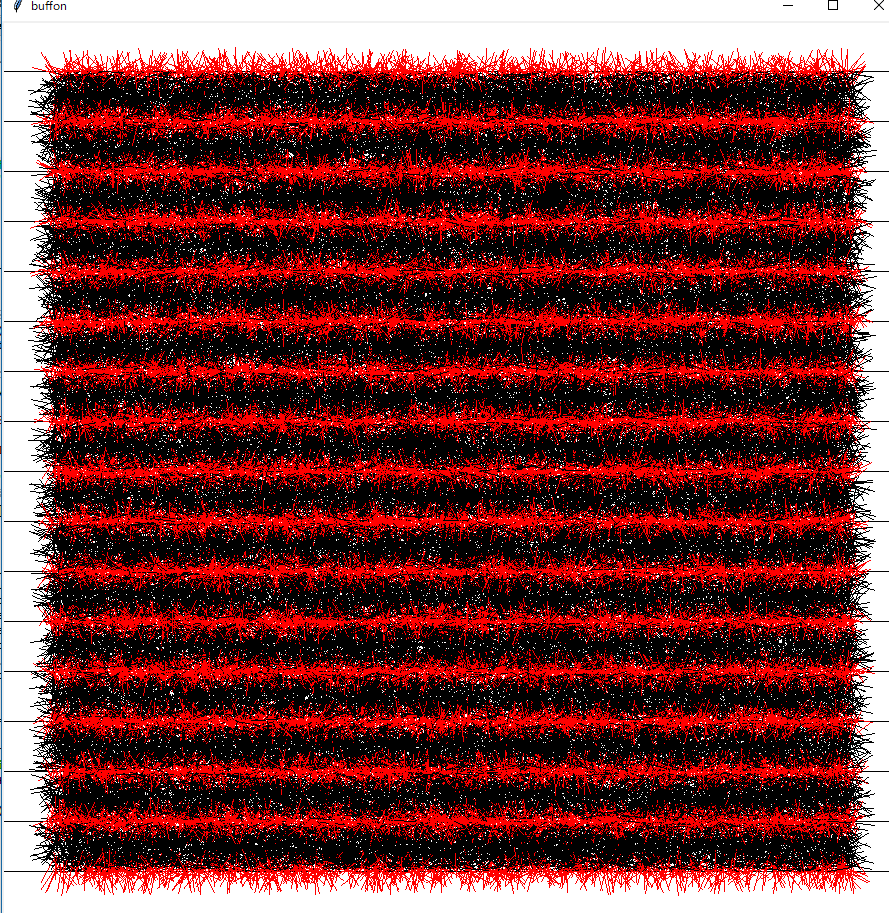
100,000本
input drop needle nubmer:100000
cross line needle:31687
n/m :3.155868337172973
10,000本くらいからいい感じに円周率によってく感じですかね。
たしかに、ビュフォンの針で円周率の近似が得られることが実感できました。
まとめ
針を100000本ばらまくと、ホラー映画みたいになるからやめようね!!