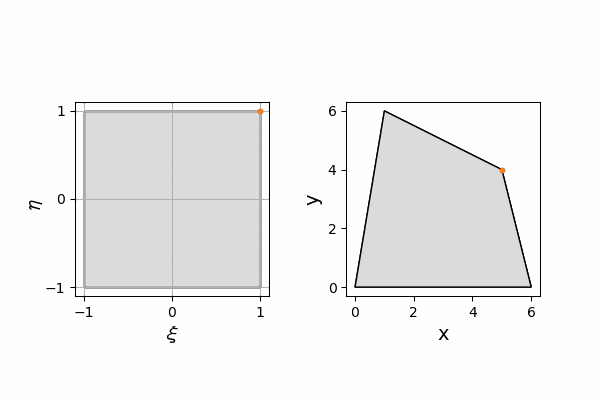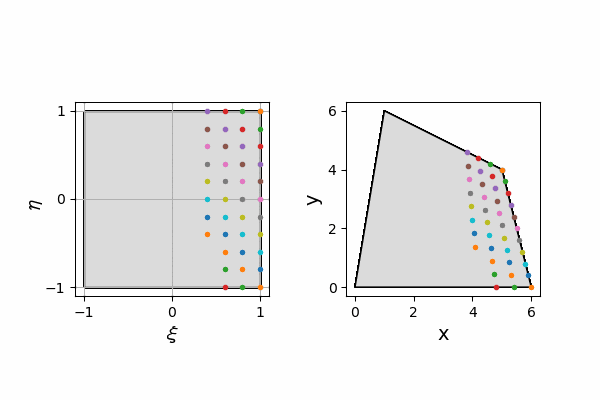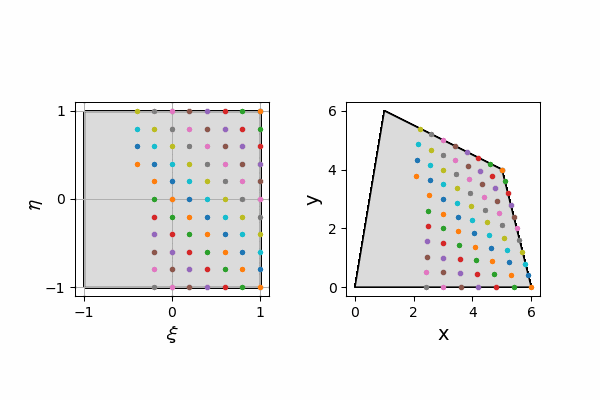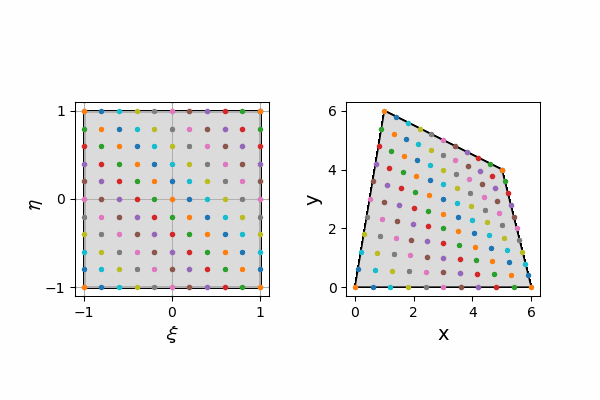有限要素法の2次元アイソパラメトリック要素の形状関数による座標変換をPythonでアニメーションにした

はじめに

有限要素法を学んでいるのですが、アイソパラメトリック要素というものが出てきて、自然座標系から物理座標へ変換する必要が出てきます。
しかし、勉強をしていて変換がとても分かりにくいという問題がありました。
そこで、変換をPythonのmatplotlibというライブラリのFuncAnimationを使用してアニメーションを作成しました。

座標の定義

今回、座標系として、
$[-1,1]\times[-1,1]$で定義された自然座標$(\xi, \eta)$、
任意範囲で定義された物理座標$(x, y)$
の2つの直交座標系を考えます。

それぞれの座標系には4節点からなる四角形があり、それぞれのの座標における節点は対応しています。
節点は自然座標における(-1,-1)の点から反時計回りに[1,2,3,4]と番号を付けます。

また、以後出てくる形状関数$N_i$についても、同じ番号の節点と対応したものとなります。

形状関数による座標変換

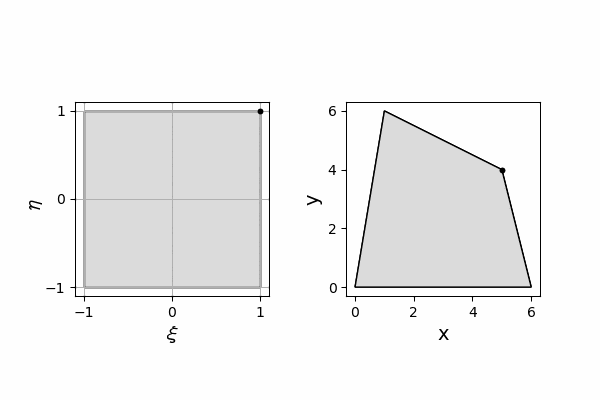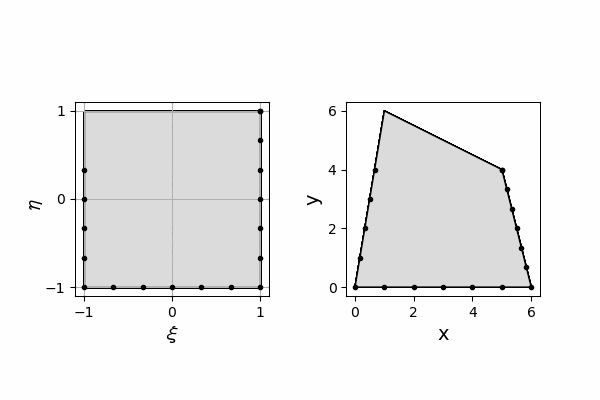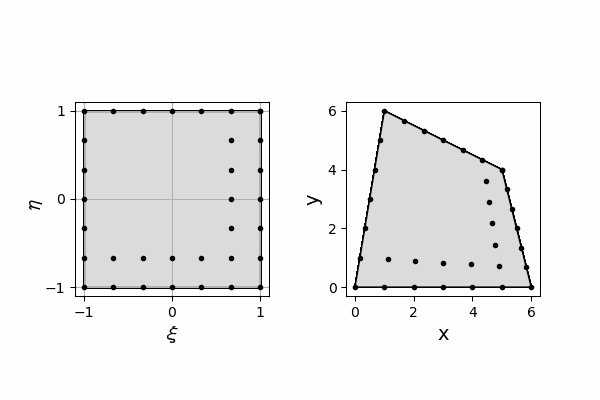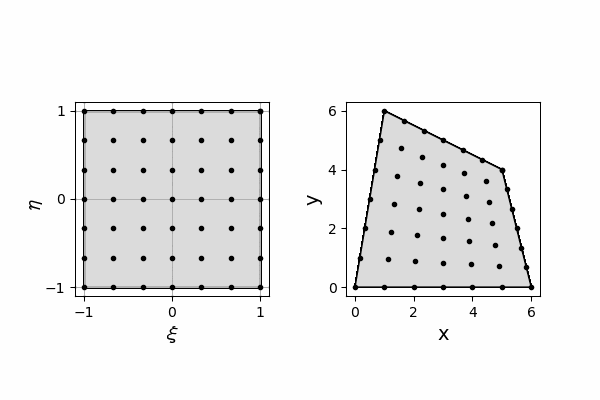
今回の目的は、$[-1,1]\times[-1,1]$で定義された自然座標の点を、任意範囲の物理座標の四角形に座標変換（写像）することです。
その際、必ず満たさなければいけないことは、有限要素法では節点に座標が設定されているため、自然座標と物理座標の節点座標が1対1対応していることです。

ここでパッと思いついたのが、ある節点で1、その他の3節点では0になるような関数です。
さらに、節点は-1か+1をとりますから、以下のような形状関数$N_i$を思いつきます。

\begin{align}
N_1(\xi, \eta)=\frac{1}{4}(1-\xi)(1-\eta) \\
N_2(\xi, \eta)=\frac{1}{4}(1+\xi)(1-\eta) \\
N_3(\xi, \eta)=\frac{1}{4}(1+\xi)(1+\eta) \\
N_4(\xi, \eta)=\frac{1}{4}(1-\xi)(1+\eta)
\end{align}

それぞれ、特定の自然座標の節点でしか1になりません。

さらに、これと物理座標の節点座標を組み合わせることで、以下のように、自然座標から物理座標に座標変換（写像）することができます。

\begin{align}
x(\xi, \eta)=&N_1(\xi, \eta)\cdot x_1+N_2(\xi, \eta)\cdot x_2+N_3(\xi, \eta)\cdot x_3+N_4(\xi, \eta)\cdot x_4 \\
y(\xi, \eta)=&N_1(\xi, \eta)\cdot y_1+N_2(\xi, \eta)\cdot y_2+N_3(\xi, \eta)\cdot y_3+N_4(\xi, \eta)\cdot y_4
\end{align}

\begin{equation}
\boldsymbol{\{x\}}=
\begin{Bmatrix} x(\xi, \eta) \\ y(\xi, \eta) \end{Bmatrix}
=\begin{bmatrix}
N_1(\xi, \eta) & N_2(\xi, \eta) & N_3(\xi, \eta) & N_4(\xi, \eta)    \\
\end{bmatrix}
\begin{Bmatrix}
x_1 & y_1 \\ 
x_2 & y_2 \\ 
x_3 & y_3 \\
x_4 & y_4
\end{Bmatrix}\\
=\begin{bmatrix}
N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4 & 0    \\
0 & N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4    \\
\end{bmatrix}
\begin{Bmatrix}
x_1 \\ y_1 \\ 
x_2 \\ y_2 \\ 
x_3 \\ y_3 \\
x_4 \\ y_4
\end{Bmatrix}\\
\end{equation}

このように式変形から導出したのではなく、形状関数が偶然発見されたようなものを、セレンディピティ要素と言います。

よく$\xi$と$\eta$の1次関数だから以下のような式から始まる行列の変形によって形状関数を導出しているものを見かけますが、こちらよりもセレンディピティ要素だからという説明のほうが個人的にはしっくりときます。

\begin{align}
x = 
\begin{bmatrix}
1 & \xi & \eta & \xi \eta
\end{bmatrix}
\begin{bmatrix}
c1\\c2\\c3\\c4
\end{bmatrix}
\end{align}

形状関数のまとめたかきかた

形状関数を書くときに、毎回以下のように4つ書くのは大変です。

\begin{align}
N_1(\xi, \eta)=\frac{1}{4}(1-\xi)(1-\eta) \\
N_2(\xi, \eta)=\frac{1}{4}(1+\xi)(1-\eta) \\
N_3(\xi, \eta)=\frac{1}{4}(1+\xi)(1+\eta) \\
N_4(\xi, \eta)=\frac{1}{4}(1-\xi)(1+\eta)
\end{align}

ある自然座標における節点$i$における座標を$(\xi_i, \eta_i)$とすれば、

\begin{align}
N_i(\xi, \eta)=\frac{1}{4}(1+\xi_i\xi)(1+\eta_i\eta) \\
\end{align}

と書くことができます。

形状関数の性質

節点の性質

形状関数では、その定義の仕方から節点では変換前後で対応があります。

辺上での性質

節点間の辺上であれば、自然座標での辺のある比での内分点が、物理座標での辺のある比での内分点に対応します。

例として、節点1と節点2の間の辺について考えましょう。
節点1と節点2では、$\eta=-1$であるため、代入すると、以下の式になります。

\begin{align}
x(\xi, \eta=-1) &=N_1(\xi, \eta=-1)\cdot x_1+N_2(\xi, \eta=-1)\cdot x_2+N_3(\xi, \eta=-1)\cdot x_3+N_4(\xi, \eta=-1)\cdot x_4 \\
&=\frac{1}{2}(1-\xi)x_1 +  \frac{1}{2}(1+\xi)x_2 \\
&= \frac{1}{2}(x_1 +x_2) + \frac{1}{2}(x_2 - x_1)\xi
\end{align}

$\frac{1}{2}(x_1 +x_2) $が辺の中点、$\frac{1}{2}(x_2 - x_1)$が辺の長さの半分であるため、辺上での内分点が対応するということがわかります。

この式が表す他の特徴は、辺上の値は両端の節点の影響しか受けないということです。
すなわち、有限要素法において辺は、半分同じ半分違う節点から構成された2つの要素と共有されますが、それぞれの要素において同じ節点から辺上の値が計算されるため、要素間で連続し、下図のような非連続な状態にはならないのです。

画像引用元　https://www.fem-vandv.net/c29.html

そして、このような連続性を満たした要素を適合要素と言います。

四角形内部の性質

四角形内部については、節点の値と形状関数によって値が計算されます。
そのため内部での値は形状関数に従うと仮定して計算されたもので、現実世界での値とは異なります。
そして、内部においては4節点すべての値から影響を受けます。

プログラム

やっと形状関数の説明が終わり、ちらほら出てきたgifを作成するプログラムの説明をします。
今回は、matplotlib.animationにあるFuncAnimationを使用して作成しました。

今回の描写プログラムは以下のようになっています。
入力する自然座標での値ij_pairと、それをisox(xi, eta, x1, x2, x3, x4)関数で変換した物理座標での値をアニメーション化しています。
変換前の四角形の節点座標はnode_xi、node_etaに格納され、
変換後の四角形の節点座標はnode_x、node_yに格納されます。

import matplotlib.pyplot as plt
import matplotlib.patches as pat
from matplotlib.animation import FuncAnimation
import numpy as np


#各形状関数
def N1(xi, eta):
    n = (1-xi)*(1-eta)/4
    return n

def N2(xi, eta):
    n = (1+xi)*(1-eta)/4
    return n

def N3(xi, eta):
    n = (1+xi)*(1+eta)/4
    return n

def N4(xi, eta):
    n = (1-xi)*(1+eta)/4
    return n

#形状関数による自然座標から物理座標への変換
def isox(xi, eta, x1, x2, x3, x4):
    x  = x1*N1(xi, eta)
    x += x2*N2(xi, eta)
    x += x3*N3(xi, eta)
    x += x4*N4(xi, eta)    
    return x




def plot_transformation(ij_pair):
    
    #自然座標の四角形（左下から）
    node_xi =[-1,1,1,-1]
    node_eta =[-1,-1,1,1]

    #物理座標の四角形（左下から）
    node_x = [0,6,5,1]
    node_y = [0,0,4,6]
    
    
    #コメントアウトで前の点が残る
    #ax[0].cla()
    #ax[1].cla()
    
    #自然座標
    ax[0].grid(b=True)
    p_xieta = pat.Polygon(xy = list(zip(node_xi,node_eta)), fc = "gainsboro", ec = "black")
    ax[0].add_patch(p_xieta)
    ax[0].set_xlabel("ξ", size = 14, fontname="MS Gothic", weight = "light")
    ax[0].set_ylabel("η", size = 14, fontname="MS Gothic", weight = "light")
    #ax[0].set_xlim(-2,2)
    #ax[0].set_ylim(-2, 2)
    ax[0].set_aspect('equal', adjustable='box')
    ax[0].set_xticks([-1,0,1])
    ax[0].set_yticks([-1,0,1])
    
    
    #物理座標
    p_xy = pat.Polygon(xy = list(zip(node_x,node_y)), fc = "gainsboro", ec = "black")
    ax[1].add_patch(p_xy)
    ax[1].set_xlabel("x", size = 14, weight = "light")
    ax[1].set_ylabel("y", size = 14, weight = "light")
    #ax[1].set_xlim(-1, 8)
    #ax[1].set_ylim(-1, 8)
    ax[1].set_aspect('equal', adjustable='box')

    #自然座標から物理座標への変換
    x = isox(*ij_pair, *node_x)
    y = isox(*ij_pair, *node_y)
    

    
    #ax[0].plot(*ij_pair, marker='.',color="black")
    #ax[1].plot(x,y,marker='.',color="black")
    
    ax[0].plot(*ij_pair, marker='.')
    ax[1].plot(x,y,marker='.')
    



#入力する自然座標の作成
ij_pair = []
for i in np.arange(-1, 1.2, 0.2)[::-1]:
    for j in np.arange(-1, 1.2, 0.2)[::-1]:        
        ij_pair.append([i,j])


fig, ax = plt.subplots(1,2, dpi=100)
plt.subplots_adjust(wspace=0.4, hspace=0.6)
anim = FuncAnimation(fig, plot_transformation, frames=ij_pair, interval=100)


anim.save("animation3.gif", writer="pillow")
plt.close()

上記のプログラムで出来上がるgifがこちらです。

ほかの点を消す

現在のプログラムでは、プロットしたすべての点が描写されています。
これを、1点のみにするには、以下の部分のコメントアウトを削除します。
これは、前フレームの描写をクリアする関数です。

    #コメントアウトで前の点が残る
    #ax[0].cla()
    #ax[1].cla()

するとこうなります。

点の色を変える

点の色が今はカラフルですが、例えば黒一色にしたいときは、これを、

    ax[0].plot(*ij_pair, marker='.')
    ax[1].plot(x,y,marker='.')

このようにして色を指定してください。

    ax[0].plot(*ij_pair, marker='.',color="black")
    ax[1].plot(x,y,marker='.',color="black")

色一覧は以下のサイトにあります。

変換後の四角形の形を変える

変換後の四角形の座標を表すnode_x、node_yをいじります。
以下のように座標を変えた結果です。

.py

    #物理座標の四角形（左下から）
    node_x = [0,4,5,3]
    node_y = [0,1,4,6]

ほかの入力

色々な入力とその変換を追ってみましょう。
プログラムは、後半のみ入れ替えています。

四角らせん

以下のサイトを参考に作成

後半.py

import itertools

LOOP = 3
WIDTH = (2*LOOP) + 1

E = (1, 0)
N = (0, -1)
W = (-1, 0)
S = (0, 1)
DIRECTION = itertools.cycle((E, N, W, S))

x = LOOP
y = LOOP
step = 1    # 進んだ距離
corner = 1  # まがり角の位置

# 二次元リストを初期化
spiral = []
for i in range(WIDTH):
    spiral.append([0 for j in range(WIDTH)])

for i in range(WIDTH * WIDTH):
    # まがり角に到達したら方向転換
    if step >= corner:
        step = 1
        direction = next(DIRECTION)
        dx, dy = direction

        # X方向に進むとき、まがり角が遠くなる
        if direction == E or direction == W:
            corner += 1
            
    spiral[y][x] = i
    step += 1
    x += dx
    y += dy



spiral = np.array(spiral)
ij_pair = []
max_index = LOOP*2
    
for i in range(WIDTH*WIDTH):
    print(np.where(spiral == i)[0][0], np.where(spiral == i)[1][0])
    ij_pair.append([np.where(spiral == i)[0][0], np.where(spiral == i)[1][0]])
    
max_index = LOOP*2
ij_pair = np.array(ij_pair)
ij_pair = (ij_pair/max_index -0.5)*2
ij_pair = ij_pair[::-1]

fig, ax = plt.subplots(1,2, dpi=100)
plt.subplots_adjust(wspace=0.4, hspace=0.6)
anim = FuncAnimation(fig, plot_transformation, frames=ij_pair, interval=100)


anim.save("rasen.gif", writer="pillow")
plt.close()

対数らせん

後半.py

ij_pair = []
for theta in range(47):
    theta /= 2
    i = 0.1*np.exp(theta/10)*np.cos(theta)
    j = 0.1*np.exp(theta/10)*np.sin(theta)
    ij_pair.append([i,j])



fig, ax = plt.subplots(1,2, dpi=100)
plt.subplots_adjust(wspace=0.4, hspace=0.6)
anim = FuncAnimation(fig, plot_transformation, frames=ij_pair, interval=100)


anim.save("rasen.gif", writer="pillow")
plt.close()

さいごに

いかがだったでしょうか。
有限要素法のわからないところを追っていたら記事が一本かけてしまいました。
他にも有限要素法の肝になってくるガウス・ルジャンドル求積については以下の記事も書いていますので、読んでみてください。

plt参考サイト

形状関数参考サイト

有限要素法関連の記事