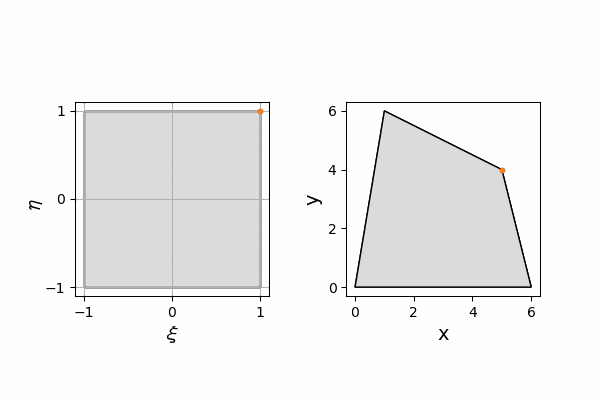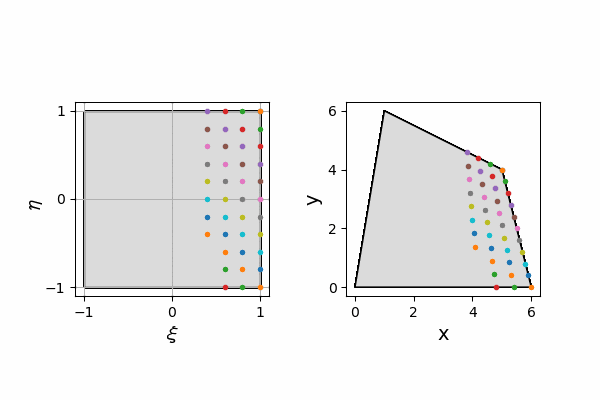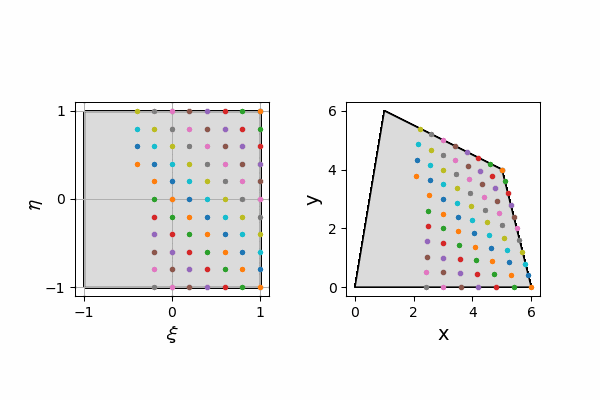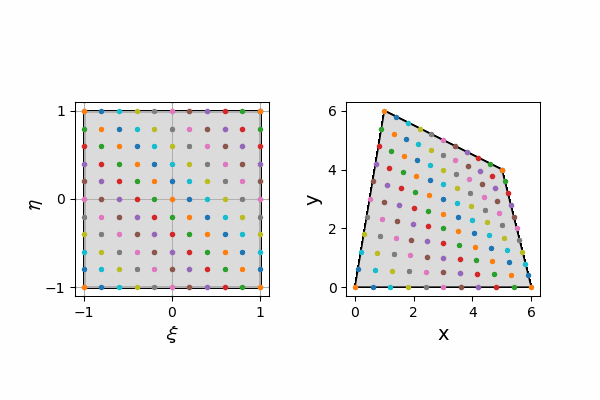はじめに
有限要素法のメッシュの一種である2次元4節点四角形要素では、アイソパラメトリック要素というものを使用します。しかし調べてみても解説サイトは少なく、理解に苦しみました。
参考にした数学的な解説は以下のサイトです。これらのサイトは詳しく、体系的に解説されています。
しかしなぜという疑問が多かったため、必要性を論じながら解説をしていきたいと思います。
なお、今回は2次元4節点の四角形要素、いわゆる四角形1次要素を扱いましたが、四角形2次要素や、3次元になっても考え方は変わません。
前提
今回計算するものは以下になります。
2次元におけるいわゆる剛性行列と言われるものです。
\begin{equation}
\boldsymbol{K}=h\iint\boldsymbol{B}^T\boldsymbol{D}\boldsymbol{B}dA
\end{equation}
ここで、$\boldsymbol{K}$は剛性行列
\begin{equation}
\boldsymbol{Ku}=\boldsymbol{F}
\end{equation}
$\boldsymbol{B}$は変位-ひずみマトリクス
\begin{equation}
\boldsymbol{\varepsilon}
=\boldsymbol{B}\boldsymbol{u}
\end{equation}
$\boldsymbol{D}$は応力-ひずみ関係式(弾性スティフネス行列、構成式)
平面応力状態での応力-ひずみ関係式
\begin{equation}
\boldsymbol{F}=
\begin{Bmatrix} \sigma_x \\ \sigma_y \\ \tau_{xy} \end{Bmatrix}
=\frac{E}{1-\nu^2}\begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & \cfrac{1-\nu}{2} \end{bmatrix}
\begin{Bmatrix} \epsilon_x \\ \epsilon_y \\ \gamma_{xy} \end{Bmatrix}
=\boldsymbol{D\varepsilon}
\end{equation}
平面ひずみ状態での応力-ひずみ関係式
\begin{equation}
\boldsymbol{F}=
\begin{Bmatrix} \sigma_x \\ \sigma_y \\ \tau_{xy} \end{Bmatrix}
=\frac{E}{(1+\nu)(1-2\nu)}\begin{bmatrix} 1-\nu & \nu & 0 \\ \nu & 1-\nu & 0 \\ 0 & 0 & \cfrac{1-2\nu}{2} \end{bmatrix}
\begin{Bmatrix} \epsilon_x \\ \epsilon_y \\ \gamma_{xy} \end{Bmatrix}
=\boldsymbol{D\varepsilon}
\end{equation}
$h$は要素の高さ(2次元での有限要素法なので、要素内の高さは一定)
$\boldsymbol{F}$は応力(Paと同じ次元)
$\boldsymbol{u}$は変位(mと同じ次元)
$\boldsymbol{\varepsilon}$はひずみ(無次元)
また、下付きのeがある場合は、特定要素での変数を表します。
1.積分の計算量を減らしたい
積分の回数
有限要素法では、メッシュを切ったそれぞれの要素ごとに以下の積分をする必要があります。
\begin{equation}
\boldsymbol{K_e}=h_e\iint\boldsymbol{B_e}^T\boldsymbol{D_e}\boldsymbol{B_e}dA_e
\end{equation}
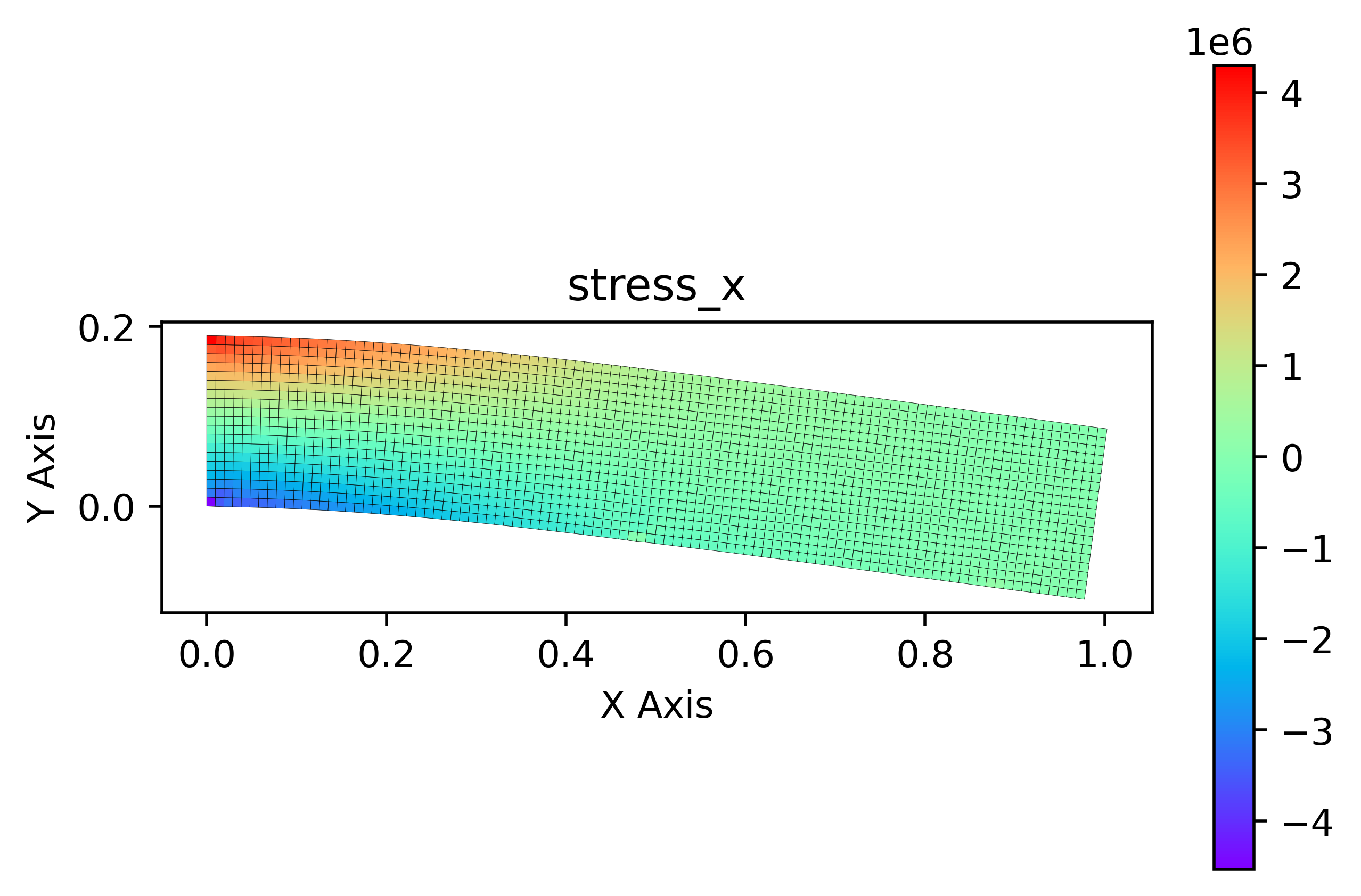
ここで要素とは、以下の画像の一つ一つの四角形のことです。
モデルが複雑になるほど、そしてメッシュを細かくするほど要素の数は増えていき、数万、数十万のオーダーの数になることもあります。
すなわち、積分する回数も数万、数十万回になります。
一回の積分の計算量
さて、それでは一回の積分の計算量はどれくらいになるでしょうか。
高校では積分は解析的に、つまり定積分をして厳密解を求めていました。
しかしコンピュータでは台形公式のように、面積の近似をします。
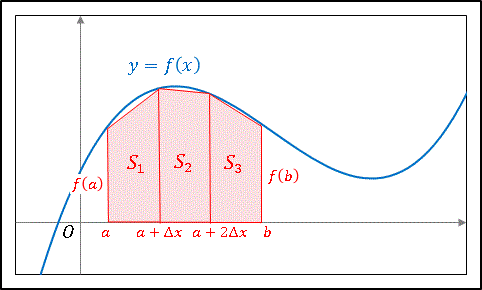
以下の画像のように、求めたい関数を分割して、台形に近似して足すことで定積分を計算します。
\begin{equation}
\int_{a}^{b}f(x)dx\simeq S_1+S_2+S_3
\end{equation}
このような計算では、台形の数を増やすほど厳密解に近づけることができ、精度が上がります。仮に台形の数を100個としても、今回扱う重積分(面積分)では100^2=10000個の足し算、3次元になって三重積分(体積積分)をするとなると100^3=1000000個の足し算となります。
つまり重積分では一回の計算回数は分割数^2回、しかも分割数によって精度は上がるがあくまで近似解というものになります。
計算回数を減らしたい
上記より、仮に一回の積分回数が10000回だとして、数万、数十万個の要素全部の積分をするとなると計算回数は数億、数十億回のオーダーとなります。
精度を上げようと台形の分割数を増やせば、面積分では2乗で効いてくるので兆のオーダーにすることもできます。
ここまでくるとコンピュータでの計算で一体どれくらいの時間がかかるのでしょうか。たとえ並列化したとしても、膨大な時間がかかることが予想されます。
積分回数は要素数分だけしなければいけないので減らすことはできません。
そのため、一回の積分における計算量を減らす必要が出てきます。
そこで、数回の計算で積分することができ、しかも精度がとても高く場合によっては厳密解を得ることもできるガウス・ルジャンドル数値積分を使用します。
まとめ
積分の計算量を減らしたいので、ガウス・ルジャンドル数値積分を使う必要が出てきた
2.ガウス・ルジャンドル数値積分
ガウス・ルジャンドル数値積分の特徴としては、関数の決まったn点の値を足すことで2n-1次多項式の積分を厳密に計算することができることです。
ガウス・ルジャンドル数値積分については、以下の記事にて詳しく解説しています。
この記事を理解しないとこの後の内容は理解できないと思われます。
重要な点は、ガウス・ルジャンドル数値積分するためには積分範囲を$[-1,1]\times[-1,1]$に写像しなければいけないという点です。
今回計算する要素剛性行列は、ガウス・ルジャンドル数値積分を使用することで以下のように計算することができます。
\begin{align}
\boldsymbol{K_e}&=h\int_A\boldsymbol{B_e}^T\boldsymbol{D_e}\boldsymbol{B_e}dA\\
&=h\int_A\boldsymbol{B_e}^T(x,y)\boldsymbol{D_e}\boldsymbol{B_e}(x,y)dxdy\\
&=h \int_{-1}^1 \int_{-1}^1 \boldsymbol{B_e}^T(\xi,\eta)\boldsymbol{D_e}\boldsymbol{B_e}(\xi,\eta)
det(\boldsymbol{J}(\xi,\eta))
d \xi d \eta \\
&= h\sum_{i=1}^n \sum_{j=1}^n w_i w_j \boldsymbol{B_e}^T(\xi_i,\eta_j)\boldsymbol{D_e}\boldsymbol{B_e}(\xi_i,\eta_j) det(\boldsymbol{J}(\xi_i,\eta_j)) \\
\end{align}
ここで、元の座標系を$(x,y)$、積分範囲である要素が$[-1,1]\times[-1,1]$で表された座標系を$(\xi,\eta)$としています。
また、写像のヤコビアンは以下のように表されます。
ヤコビアンがわからない人は、微積分の重積分を復習してください。
\begin{equation}
\boldsymbol{J}(\xi, \eta) =
\frac{\partial (x,y)}{\partial (\xi, \eta)} =
\begin{Bmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} \\
\frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} \\
\end{Bmatrix}
\end{equation}
必要性その1
上記の計算をするためにも、まず、以下のヤコビ行列式を求める必要があります。
\begin{equation}
det(\boldsymbol{J}(\xi, \eta)) =
\begin{vmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} \\
\frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} \\
\end{vmatrix}
\end{equation}
そのためにも、元の座標系$(x,y)$と$[-1,1]\times[-1,1]$で表された座標系$(\xi,\eta)$の積分範囲の関係を定義する必要があります。
すなわち、積分範囲の座標変換(写像)を定義する必要があります。
必要性その2
$\boldsymbol{B_e}$は要素内の位置の関数のため、座標系によって値が変わります。
すなわち、元の座標系での$\boldsymbol{B_e}(x,y)$を、$[-1,1]\times[-1,1]$の座標系での$\boldsymbol{B_e}(\xi,\eta)$に変形する必要があります。
言い換えれば、要素内の任意の点における$\boldsymbol{B_e}(x,y)$と$\boldsymbol{B_e}(\xi,\eta)$の関係を知る必要があります。
まとめ
座標変換するので、
1.ヤコビ行列式を求めるためにも座標変換を定義する必要がある
2.$\boldsymbol{J}(\xi,\eta)$が必要なので、$\boldsymbol{B_e}(x,y)$と$\boldsymbol{B_e}(\xi,\eta)$の関係を知る必要がある
3. 座標変換(積分範囲の写像)
元の座標系$(x,y)$と$[-1,1]\times[-1,1]$で表された座標系$(\xi,\eta)$の関係を決めます。
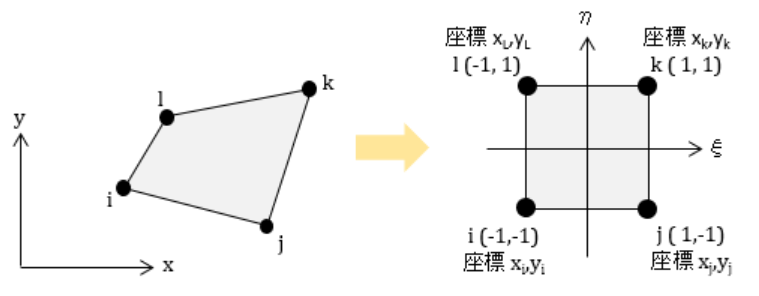
座標変換(写像)では、元の座標の四角形の頂点が変換後の四角形の頂点に対応するように変換することにします。
すなわち、下のgifのような変換をします。
座標変換(写像)は、$(\xi,\eta)$から$(x,y)$への写像と、$(x,y)$から$(\xi,\eta)$への写像の二通りの考え方があります。
今回、以下のヤコビ行列式を計算しなければいけないため、$(\xi,\eta)$から$(x,y)$への写像、すなわち$(x,y)$を$(\xi,\eta)$で表すことにします。
\begin{equation}
det(\boldsymbol{J}(\xi, \eta)) =
\begin{vmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} \\
\frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} \\
\end{vmatrix}
\end{equation}
おそらく数ある写像のうち、一番適した方法が以下のような形状関数$N_i$を使用した方法です。
なお$x_i,y_i$は要素ごとに定まるので定数です。
このメリットは、適合要素であることです。
\begin{align}
N_1(\xi, \eta)=\frac{1}{4}(1-\xi)(1-\eta) \\
N_2(\xi, \eta)=\frac{1}{4}(1+\xi)(1-\eta) \\
N_3(\xi, \eta)=\frac{1}{4}(1+\xi)(1+\eta) \\
N_4(\xi, \eta)=\frac{1}{4}(1-\xi)(1+\eta)
\end{align}
\begin{align}
x(\xi, \eta)=&N_1(\xi, \eta)\cdot x_1+N_2(\xi, \eta)\cdot x_2+N_3(\xi, \eta)\cdot x_3+N_4(\xi, \eta)\cdot x_4 \\
y(\xi, \eta)=&N_1(\xi, \eta)\cdot y_1+N_2(\xi, \eta)\cdot y_2+N_3(\xi, \eta)\cdot y_3+N_4(\xi, \eta)\cdot y_4
\end{align}
この写像についての詳しい話は以下の記事で解説していますので、ぜひ読んでください。
ヤコビ行列式の計算
今回の目的は、以下を計算することでした。
\begin{equation}
det(\boldsymbol{J}(\xi, \eta)) =
\begin{vmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} \\
\frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} \\
\end{vmatrix}
\end{equation}
まずそれぞれの形状関数を$\xi, \eta$で微分したものは、以下のようになります。
\begin{align}
&\cfrac{\partial N_1}{\partial \xi}=-\cfrac{1}{4}(1-\eta) &&\cfrac{\partial N_2}{\partial \xi}=+\cfrac{1}{4}(1-\eta) & &\cfrac{\partial N_3}{\partial \xi}=+\cfrac{1}{4}(1+\eta) & &\cfrac{\partial N_4}{\partial \xi}=-\cfrac{1}{4}(1+\eta) \\
&\cfrac{\partial N_1}{\partial \eta}=-\cfrac{1}{4}(1-\xi) &&\cfrac{\partial N_2}{\partial \eta}=-\cfrac{1}{4}(1+\xi) & &\cfrac{\partial N_3}{\partial \eta}=+\cfrac{1}{4}(1+\xi) & &\cfrac{\partial N_4}{\partial \eta}=+\cfrac{1}{4}(1-\xi)
\end{align}
よって、ヤコビ行列の各要素の値は以下のように求まります。
なお$x_i,y_i$は要素ごとに定まるので定数です。
\begin{align}
\cfrac{\partial x}{\partial \xi}
&=\cfrac{\partial N_1}{\partial \xi}x_1+\cfrac{\partial N_2}{\partial \xi}x_2+\cfrac{\partial N_3}{\partial \xi}x_3+\cfrac{\partial N_4}{\partial \xi}x_4
=-\cfrac{1}{4}(1-\eta)x_1 + \cfrac{1}{4}(1-\eta)x_2 +\cfrac{1}{4}(1+\eta)x_3 - \cfrac{1}{4}(1+\eta)x_4 \\
\cfrac{\partial x}{\partial \eta}
&=\cfrac{\partial N_1}{\partial \eta}x_1+\cfrac{\partial N_2}{\partial \eta}x_2+\cfrac{\partial N_3}{\partial \eta}x_3+\cfrac{\partial N_4}{\partial \eta}x_4
=-\cfrac{1}{4}(1-\xi)x_1 - \cfrac{1}{4}(1+\xi)x_2 +\cfrac{1}{4}(1+\xi)x_3 + \cfrac{1}{4}(1-\xi)x_4 \\
\cfrac{\partial y}{\partial \xi}
&=\cfrac{\partial N_1}{\partial \xi}y_1+\cfrac{\partial N_2}{\partial \xi}y_2+\cfrac{\partial N_3}{\partial \xi}y_3+\cfrac{\partial N_4}{\partial \xi}y_4
=-\cfrac{1}{4}(1-\eta)y_1 + \cfrac{1}{4}(1-\eta)y_2 +\cfrac{1}{4}(1+\eta)y_3 - \cfrac{1}{4}(1+\eta)y_4 \\
\cfrac{\partial y}{\partial \eta}
&=\cfrac{\partial N_1}{\partial \eta}y_1+\cfrac{\partial N_2}{\partial \eta}y_2+\cfrac{\partial N_3}{\partial \eta}y_3+\cfrac{\partial N_4}{\partial \eta}y_4
=-\cfrac{1}{4}(1-\xi)y_1 - \cfrac{1}{4}(1+\xi)y_2 +\cfrac{1}{4}(1+\xi)y_3 + \cfrac{1}{4}(1-\xi)y_4 \\
\end{align}
行列で書くともっとすっきりします。
\begin{equation}
\boldsymbol{J}(\xi,\eta)
=\begin{bmatrix}
\frac{\partial x}{\partial \xi} &\frac{\partial y}{\partial \xi} \\
\frac{\partial x}{\partial \eta} &\frac{\partial y}{\partial \eta}\\
\end{bmatrix}
=\begin{bmatrix}
\frac{\partial N_1}{\partial \xi} & \frac{\partial N_2}{\partial \xi} & \frac{\partial N_3}{\partial \xi} &\frac{\partial N_4}{\partial \xi}\\
\frac{\partial N_1}{\partial \eta} & \frac{\partial N_2}{\partial \eta} & \frac{\partial N_3}{\partial \eta} &\frac{\partial N_4}{\partial \eta}\\
\end{bmatrix}
\begin{bmatrix}
x_1 & y_1\\
x_2 & y_2\\
x_3 & y_3\\
x_4 & y_4\\
\end{bmatrix}
=\begin{bmatrix}
-\cfrac{1}{4}(1-\eta) & +\cfrac{1}{4}(1-\eta) & +\cfrac{1}{4}(1+\eta) & -\cfrac{1}{4}(1+\eta) \\
-\cfrac{1}{4}(1-\xi) &-\cfrac{1}{4}(1+\xi) & +\cfrac{1}{4}(1+\xi) & +\cfrac{1}{4}(1-\xi)
\end{bmatrix}
\begin{bmatrix}
x_1 & y_1\\
x_2 & y_2\\
x_3 & y_3\\
x_4 & y_4\\
\end{bmatrix}
\end{equation}
よって以上から、任意の点でのヤコビ行列式を計算することができます。
まとめ
座標変換を形状関数によって定義し、ヤコビ行列式も求まった
4.内挿関数
最後に、要素内の任意の点における$\boldsymbol{B_e}(x,y)$と$\boldsymbol{B_e}(\xi,\eta)$の関係を求めましょう。
内挿とひずみ-変位マトリクス
そもそも、有限要素法では、節点でのみ変位と応力を持っており、それぞれを節点ごとに計算します。
そして、節点以外の場所では変位を近くの節点の値から補間、内挿することで変位場を仮定しています。
大事なことは、内挿関数により仮定した変位場から、ひずみ-変位マトリクス$\boldsymbol{B_e}$を求めることができます。
今回は座標系が二つありますが、実際に計算で使用するのは$(\xi,\eta)$座標系の$\boldsymbol{B_e}(\xi,\eta)$です。
\begin{align}
\boldsymbol{K_e}&=h\int_A\boldsymbol{B_e}^T\boldsymbol{D_e}\boldsymbol{B_e}dA\\
&=h\int_A\boldsymbol{B_e}^T(x,y)\boldsymbol{D_e}\boldsymbol{B_e}(x,y)dxdy\\
&=h \int_{-1}^1 \int_{-1}^1 \boldsymbol{B_e}^T(\xi,\eta)\boldsymbol{D_e}\boldsymbol{B_e}(\xi,\eta)
det(\boldsymbol{J}(\xi,\eta))
d \xi d \eta \\
&= h\sum_{i=1}^n \sum_{j=1}^n w_i w_j \boldsymbol{B_e}^T(\xi_i,\eta_j)\boldsymbol{D_e}\boldsymbol{B_e}(\xi_i,\eta_j) det(\boldsymbol{J}(\xi_i,\eta_j)) \\
\end{align}
普通は、実際の座標系である$(x,y)$で変位場を内挿することで仮定し、$\boldsymbol{B_e}(x,y)$を求めた後に、座標変換により$\boldsymbol{B_e}(\xi,\eta)$を求めることを考えます。
しかし、アイソパラメトリック要素を使用した有限要素法では、
どうせ$(x,y)$座標から$(\xi,\eta)$座標に座標変換するなら、内挿を$(\xi,\eta)$座標でしてしまえばいいではないかという考えのもと計算をしています。
すなわち、変位$u,v$を以下のように$(\xi,\eta)$座標系で内挿関数$N_i$を使用して内挿します。
\begin{align}
u(\xi, \eta)=&N_1(\xi, \eta)\cdot u_1+N_2(\xi, \eta)\cdot u_2+N_3(\xi, \eta)\cdot u_3+N_4(\xi, \eta)\cdot u_4 \\
v(\xi, \eta)=&N_1(\xi, \eta)\cdot v_1+N_2(\xi, \eta)\cdot v_2+N_3(\xi, \eta)\cdot v_3+N_4(\xi, \eta)\cdot v_4
\end{align}
さらに、この内挿関数$N_i$は形状関数と同じものを使えるから使ってしまえ、というものがアイソパラメトリック要素です。
\begin{align}
N_1(\xi, \eta)=\frac{1}{4}(1-\xi)(1-\eta) \\
N_2(\xi, \eta)=\frac{1}{4}(1+\xi)(1-\eta) \\
N_3(\xi, \eta)=\frac{1}{4}(1+\xi)(1+\eta) \\
N_4(\xi, \eta)=\frac{1}{4}(1-\xi)(1+\eta)
\end{align}
しかし、内挿を$(\xi,\eta)$座標でしてしまったら$\boldsymbol{B_e}(x,y)$がわからず、$(x,y)$座標系での要素内の変位場やひずみ場、応力場ががわからないのでは、という疑問がわくかもしれません。
しかし、まず第一に有限要素法では、要素における平均的なひずみ、応力を使用して色を塗ったりしており、$(x,y)$座標系でのひずみ場、応力場は必要がありません。実際の計算では、積分点でのひずみ、応力のみ計算をし、さらにその平均をとることで要素内でのひずみ、応力の平均値を求めることができます。
第二に、仮に$(x,y)$座標での変位場が必要になっても、$(\xi,\eta)$座標からの座標変換により求めることができます。
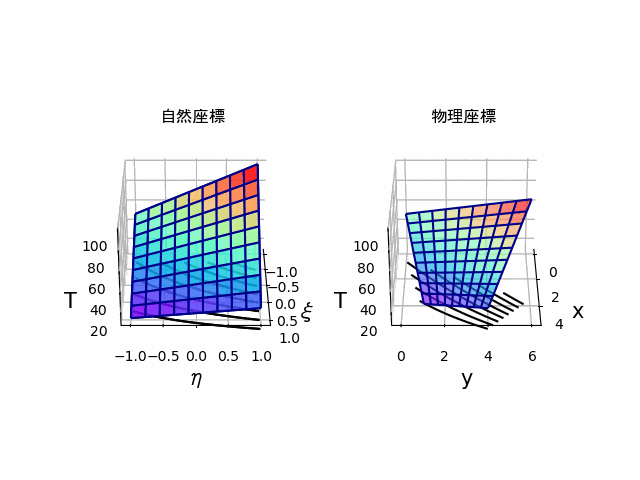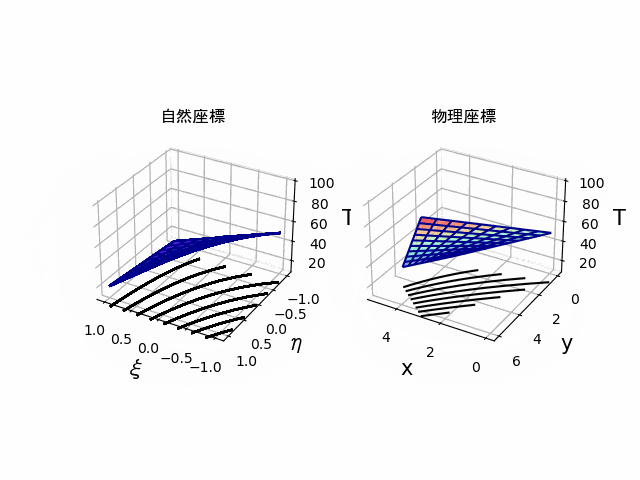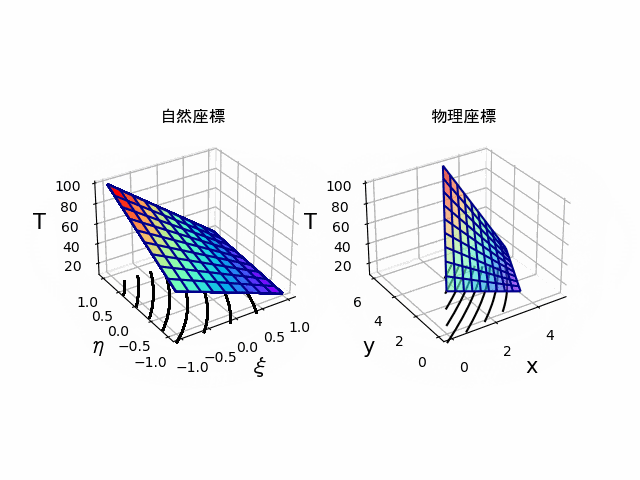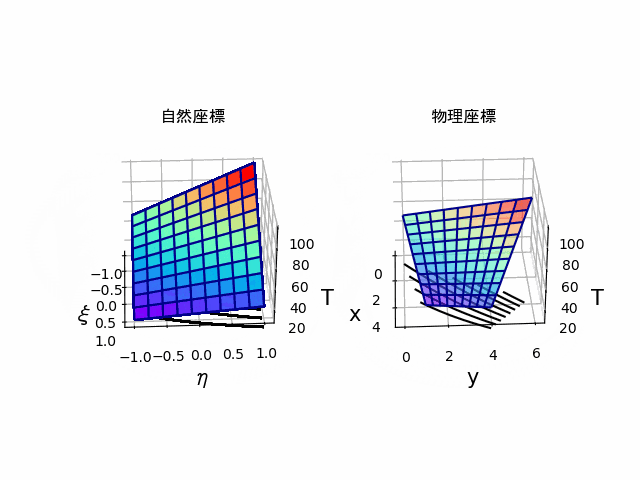
実際に内挿関数と形状関数に同じ関数を使用して、$(\xi,\eta)$座標で内挿した温度分布と、それを座標変換したものを並べたものが以下になります。
詳しくはこちらの記事をご覧ください。
ひずみ-変位マトリクスの計算
ひずみ-変位マトリクス$\boldsymbol{B}$は、今回のような内挿関数を使用した場合、以下のように表されます。
\begin{equation}
\boldsymbol{\varepsilon}=\begin{Bmatrix} \cfrac{\partial u}{\partial x} \\ \cfrac{\partial v}{\partial y} \\ \cfrac{\partial u}{\partial y}+\cfrac{\partial v}{\partial x} \end{Bmatrix}
=\begin{bmatrix}
\cfrac{\partial N_1}{\partial x} & 0 & \cfrac{\partial N_2}{\partial x} & 0 & \cfrac{\partial N_3}{\partial x} & 0 & \cfrac{\partial N_4}{\partial x} & 0 \\
0 & \cfrac{\partial N_1}{\partial y} & 0 & \cfrac{\partial N_2}{\partial y} & 0 & \cfrac{\partial N_3}{\partial y} & 0 & \cfrac{\partial N_4}{\partial y} \\
\cfrac{\partial N_1}{\partial y} & \cfrac{\partial N_1}{\partial x} & \cfrac{\partial N_2}{\partial y} & \cfrac{\partial N_2}{\partial x} & \cfrac{\partial N_3}{\partial y} & \cfrac{\partial N_3}{\partial x} & \cfrac{\partial N_4}{\partial y} & \cfrac{\partial N_4}{\partial x}
\end{bmatrix}
\begin{Bmatrix}
u_i \\ v_i \\ u_j \\ v_j \\ u_k \\ v_k \\ u_l \\ v_l
\end{Bmatrix}
=\boldsymbol{B}\boldsymbol{u}
\end{equation}
すなわち、ひずみ-変位マトリクス$\boldsymbol{B}$を求めるためには、この行列の各要素を求める必要があります。
\begin{equation}
\begin{bmatrix}
\frac{\partial N_1}{\partial x} & \frac{\partial N_2}{\partial x} & \frac{\partial N_3}{\partial x} &\frac{\partial N_4}{\partial x}\\
\frac{\partial N_1}{\partial y} & \frac{\partial N_2}{\partial y} & \frac{\partial N_3}{\partial y} &\frac{\partial N_4}{\partial y}\\
\end{bmatrix}
\end{equation}
内挿関数$N_i$は$(\xi,\eta)$座標で定義した$N_i(\xi,\eta)$なので、直接$(x,y)$では偏微分できません。そのため、高校の微積で習う、合成関数の微分をする必要があります。
\begin{equation}
\begin{bmatrix}
\frac{\partial N_1}{\partial x} & \frac{\partial N_2}{\partial x} & \frac{\partial N_3}{\partial x} &\frac{\partial N_4}{\partial x}\\
\frac{\partial N_1}{\partial y} & \frac{\partial N_2}{\partial y} & \frac{\partial N_3}{\partial y} &\frac{\partial N_4}{\partial y}\\
\end{bmatrix}
=\begin{bmatrix}
\frac{\partial N_1}{\partial \xi} \frac{\partial \xi}{\partial x} + \frac{\partial N_1}{\partial \eta} \frac{\partial \eta}{\partial x}
& \frac{\partial N_2}{\partial \xi} \frac{\partial \xi}{\partial x} + \frac{\partial N_2}{\partial \eta} \frac{\partial \eta}{\partial x}
& \frac{\partial N_3}{\partial \xi} \frac{\partial \xi}{\partial x} + \frac{\partial N_3}{\partial \eta} \frac{\partial \eta}{\partial x}
&\frac{\partial N_4}{\partial \xi} \frac{\partial \xi}{\partial x} + \frac{\partial N_4}{\partial \eta} \frac{\partial \eta}{\partial x}
\\
\frac{\partial N_1}{\partial \xi} \frac{\partial \xi}{\partial y} + \frac{\partial N_1}{\partial \eta} \frac{\partial \eta}{\partial y}
& \frac{\partial N_2}{\partial \xi} \frac{\partial \xi}{\partial y} + \frac{\partial N_2}{\partial \eta} \frac{\partial \eta}{\partial y}
& \frac{\partial N_3}{\partial \xi} \frac{\partial \xi}{\partial y} + \frac{\partial N_3}{\partial \eta} \frac{\partial \eta}{\partial y}
&\frac{\partial N_4}{\partial \xi} \frac{\partial \xi}{\partial y} + \frac{\partial N_4}{\partial \eta} \frac{\partial \eta}{\partial y} \\
\end{bmatrix}
\\
=\begin{bmatrix}
\frac{\partial \xi}{\partial x} &\frac{\partial \eta}{\partial x} \\
\frac{\partial \eta}{\partial y} &\frac{\partial \eta}{\partial y}\\
\end{bmatrix}
\begin{bmatrix}
\frac{\partial N_1}{\partial \xi} & \frac{\partial N_2}{\partial \xi} & \frac{\partial N_3}{\partial \xi} &\frac{\partial N_4}{\partial \xi}\\
\frac{\partial N_1}{\partial \eta} & \frac{\partial N_2}{\partial \eta} & \frac{\partial N_3}{\partial \eta} &\frac{\partial N_4}{\partial \eta}\\
\end{bmatrix}
=\begin{bmatrix}
\frac{\partial x}{\partial \xi} &\frac{\partial y}{\partial \xi} \\
\frac{\partial x}{\partial \eta} &\frac{\partial y}{\partial \eta}\\
\end{bmatrix}^{-1}
\begin{bmatrix}
\frac{\partial N_1}{\partial \xi} & \frac{\partial N_2}{\partial \xi} & \frac{\partial N_3}{\partial \xi} &\frac{\partial N_4}{\partial \xi}\\
\frac{\partial N_1}{\partial \eta} & \frac{\partial N_2}{\partial \eta} & \frac{\partial N_3}{\partial \eta} &\frac{\partial N_4}{\partial \eta}\\
\end{bmatrix}
\\
=\boldsymbol{J}^{-1}\boldsymbol{H}
\end{equation}
そうすると、適当に$\boldsymbol{H}$と置いていますが、このように座標変換の時に求めた行列で$\boldsymbol{B_e}(\xi,\eta)$を求めることができます。
まとめ
1.座標変換で使用した形状関数と同じ関数を内挿関数として使用した
2.$\boldsymbol{B_e}(\xi,\eta)$が必要だから座標変換せずに$(\xi,\eta)$座標系で直接内挿した
5.アイソパラメトリック要素
アイソパラメトリックとは、アイソ+パラメトリックの2語から成り立っています。
まずパラメトリック要素とは、前述のように、$(\xi,\eta)$座標系でいろいろ要素の値を決定して$(x,y)$座標系に変換するという要素です。
実際に今回は、要素内の座標を$(\xi,\eta)$座標系で定義し、また要素内の変位場も$(\xi,\eta)$座標系で内挿して決定しており、実際の$(x,y)$座標系では特に定義していません。
中でも、内挿関数において座標変換と同じ形状関数を使用した要素をアイソパラメトリック要素と呼びます。
アイソ(iso) つまり同じという意味です。
同じ関数を使用することで、計算時に同じプログラムを使用できるというメリットがあります。
なお、サブパラメトリック要素、スーパーパラメトリック要素というものもあるようです。
まとめ
アイソパラメトリック要素について、必要性の観点から説明をしました。
まとめると、
積分の計算量を減らすためにガウス・ルジャンドル数値積分を導入し、使用するためにもパラメトリック要素を使用しなければならず、また形状関数で座標変換を定義して同様の関数を内挿関数として使用してアイソパラメトリック要素とする
というものでした。
今回は2次元4節点の四角形要素、いわゆる1次要素を扱いましたが、四角形2次要素になっても形状関数がちょっと変わるだけで特に難しくはありません。
詳しくはこちらのサイトを見てください。
また、3次元になったも基本的な考え方は変わりません。形状関数の変数が3つになり、各計算を3次元に対応させるだけです。
新たに有限要素法を学ぶ人の参考になったらうれしいです。
有限要素法関連の記事