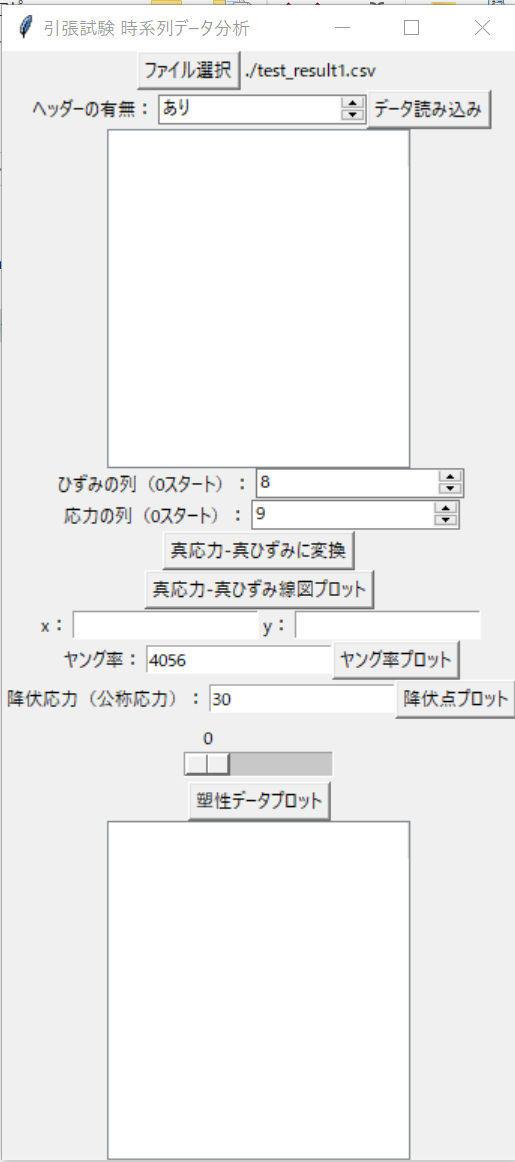
はじめに
有限要素法(FEM)で塑性する材料を扱おうとすると、塑性挙動として塑性ひずみとその時の応力を入力する必要があります。
しかしこの値を実験データから計算して求めるのは大変です。
例えばAbaqusではキャリブレーションという機能で取得できるのですが、入力する点数が多いとまあ読み込みが重くて時間がかかってしまうという問題がありました。
そこでPythonを使って同じような機能のGUIアプリが欲しいと思い、Tkinterを使用して作成をしました。
実際に作成したものが以下のものとなり、ひずみと応力のcsvファイルを選択し、ヤング率と降伏応力を入力してやれば任意の点数の塑性ひずみと応力のペアが出力されます。
プログラムは最近話題の自然言語の生成AIにベースを書いてもらい、修正して作成しました。
コードは以下で配布しています
使い方
基本的には上からポチポチボタンを押していけばできます。
用意するもの
- ひずみと応力が書かれたcsvファイル
- ヤング率
注意
- 単位系はひずみは無次元[-]、応力・ヤング率は[MPa]をイメージしていますが、特に単位変換の演算はしていません。
- csvデータは降伏点からヤング率で伸ばした線が原点を通るようなデータに変換してください。
- 降伏点は入力値と最も近い公称応力の点選ばれます。
中身の計算
試験の応力ひずみ線図から塑性ひずみと応力のペアを計算するためには、以下の作業が必要です。
これ以外にも生データからSI単位系に変換したり、ノイズを除去したり、原点をずらして片当たり分を削除したりなどいろいろありますが、ここでは割愛します。
公称応力・ひずみから真応力・ひずみへの変換
普通、引張試験などのデータから直接取得・計算した値は、公称応力・ひずみと呼ばれるもので、試験片の変形を考えていません。
一方で有限要素法の材料特性には、試験片の断面積変化を考えた、本当の材料の硬化特性を再現するために真応力・ひずみの形式にする必要があります。
詳しくは材料力学の教科書を復習するか、以下の論文を読んでください。
ここで公称応力・ひずみから真応力・ひずみへの変換は以下の式で計算できます。
$$
\text{真ひずみ}=\ln(1+\text{公称ひずみ})\
$$
$$
\text{真応力}=\text{公称応力}*(1+\text{真ひずみ})
$$
塑性ひずみの計算
ひずみは弾性ひずみと塑性ひずみに分けることができ、このうち応力上昇に効いてくるものは弾性ひずみです。そのため、同じ真ひずみでも塑性ひずみが大きい方が応力は小さくなります。これが塑性の特徴です。
こちらについても詳しくは以下の論文などに書いています。
ここで塑性ひずみを計算するためには、以下のように計算する必要があります。
$
(\textrm{真ひずみ} - \textrm{塑性ひずみ} ) \times \textrm{ヤング率} = \textrm{弾性ひずみ} \times \textrm{ヤング率} = \textrm{真応力}
$
よって
$
\textrm{塑性ひずみ} = \textrm{真ひずみ} - \frac{\textrm{真応力}}{\textrm{ヤング率}}
$
ChatGPTの利用
BingのCopilotであったり、GooggleのCodeGenmmaを使用してベースとなるプログラムを書いてみました。
あなたは、Pythonに精通しているアプリケーションエンジニアです
pythonで引張試験の時系列データから降伏応力と塑性ひずみを取得するGUIアプリをTkinterで作ってください。
このアプリでは、以下のことを実行します。
データの読み込みと前処理:
CSVファイルを読み込みます。ヘッダーの有無と何列目がひずみか応力かを指定するスピンボタンを実装します。
ひずみをln(1+ひずみ)で真ひずみに変換します。
応力を応力*(1+真ひずみ)で真応力に変換します。
データの可視化:
真応力を縦軸、真ひずみを横軸としてプロットします。
マウスでクリックした座標に最も近い点と原点を結ぶ直線の傾きを求め、ヤング率とします。
ヤング率を変更できるように入力ボックスを作成します
ヤング率を傾きとして原点を通る線をプロットします。
降伏点の表示と塑性データ点の計算:
マウスでクリックした座標に最も近い点を降伏点として表示します。
降伏点を変更できるように入力ボックスを作成します
降伏点から最後の点までをn分割した点群を別の色で表示し、これを塑性データ点とします。nはシークバーで調整可能です。
各塑性データ点において、塑性ひずみを(真ひずみ - 真応力/ヤング率)で計算し、塑性ひずみと真応力を表形式で表示します。
なお、プロンプトの書き方は以下の記事を参考にしましたが、一発で完全なプログラムは出力されなかったのでまだまだ改善の余地はありそうです。
しかし、Tkinterを一度も使ったことのない私でも少し直すだけで動くようになるベースはできており、生成AIを使ったかいがありました。
プログラムの解説
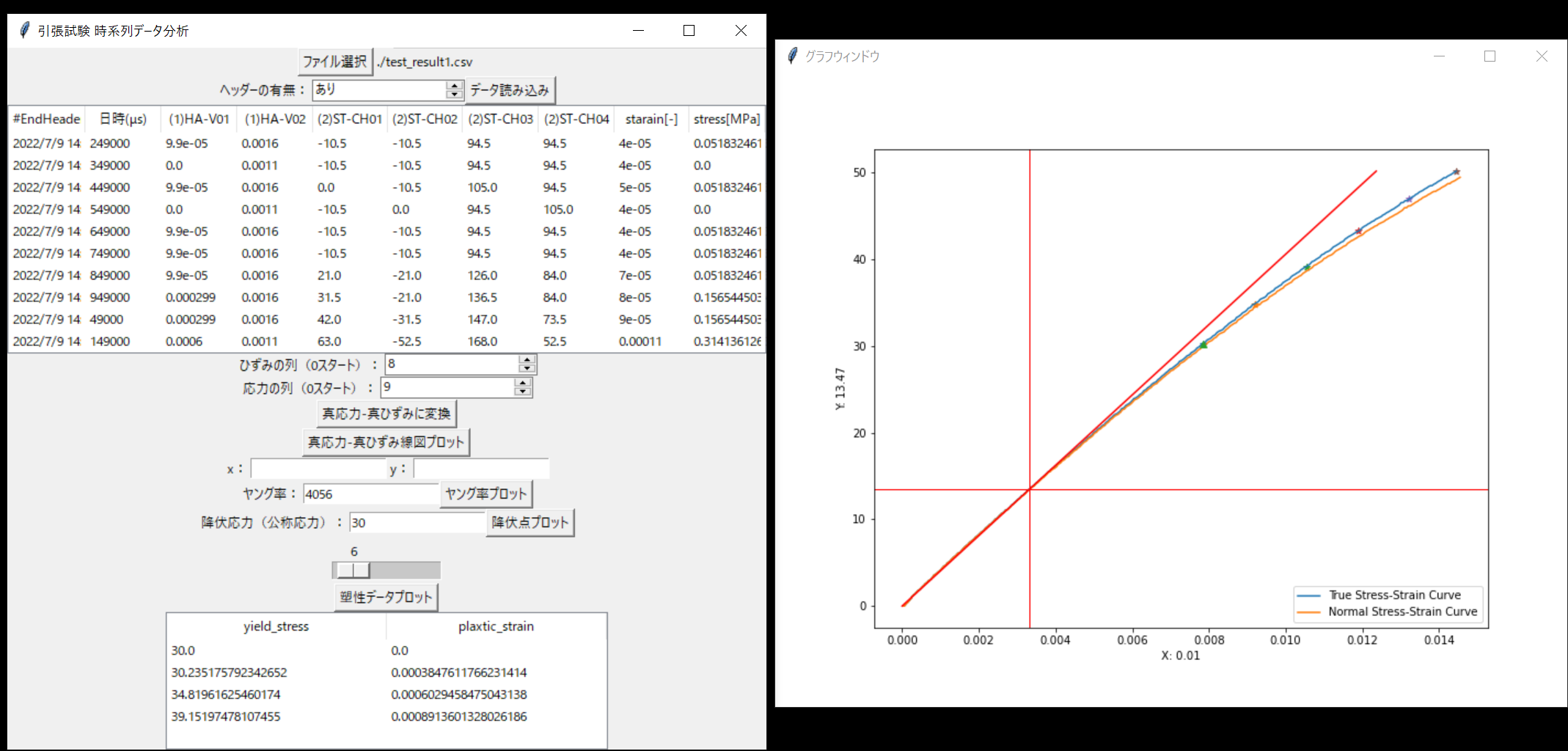
この Python コードは、ひずみと応力のデータが書かれたcsvデータファイルを選択し、データを読み込み、真応力-真ひずみの曲線を作成し、ヤング率や降伏点を指定し、任意点数の塑性ひずみと真応力のペアを得ることができます。
Tkinterで作成したGUIは以下のようになっており、上から順に解説していきます。
ウィンドウの生成
本アプリは、グラフのみを表示するウィンドウと、ボタンを押したり値を入力するウィンドウに分かれています。
グラフサイズを大きくしたい場合は、figsize=(10, 8)となっている部分を大きくしてください。
# グラフを表示するウィンドウの作成
def create_graph_window(self, master):
graph_window = tk.Toplevel(master)
graph_window.title('グラフウィンドウ')
# matplotlibのFigureを作成
self.figure, self.ax = plt.subplots(figsize=(10, 8))
self.canvas = FigureCanvasTkAgg(self.figure, master=graph_window)
self.canvas.get_tk_widget().pack()
データの読み込み及び表示
まず開くファイルを選択するために、select_file()関数でtkinterのfiledialog.askopenfilename()という関数を使用しています。
これを使うだけで自動的にエクスプローラーが開かれて簡単にファイルを選択することができ、初心者にありがちな「ディレクトリ?なにそれ?」というのを回避しています。
次に、load_data()関数でpandasを使用してcsvファイルを開いています。
また、ここでヘッダーのありなしをGUIでの選択で決めています。
最後に、データをdisplay_table()で表示しています。
def select_file(self):
self.file_path = filedialog.askopenfilename()
self.lbl_file["text"] = self.file_path
def display_table(self, df, tree):
tree.delete(*tree.get_children())
print(df)
tree["column"] = list(df.columns)
tree["show"] = "headings"
for column in tree["column"]:
tree.heading(column, text=column)
df_rows = df.to_numpy().tolist()
for row in df_rows:
tree.insert("", "end", values=row)
# データ読み込み
def load_data(self):
# CSV ファイルをロードし、データフレームを作成します
header = self.spinbox_header.get()
print(self.file_path)
if header == "あり":
self.data_frame = pd.read_csv(self.file_path, header=0)
else:
self.data_frame = pd.read_csv(self.file_path, header=None)
self.display_table(self.data_frame, self.tree)
"""
self.tree["column"] = list(self.data_frame.columns)
self.tree["show"] = "headings"
for column in self.tree["column"]:
self.tree.heading(column, text=column)
df_rows = self.data_frame.to_numpy().tolist()
for row in df_rows:
self.tree.insert("", "end", values=row)
"""
公称応力・ひずみから真応力・ひずみへの変換
GUIで選択された公称応力・公称ひずみを示す列の番号を取得し、transform_data()ではその列を使用して真応力・ひずみを計算しています。
def transform_data(self):
# ひずみと応力を真値に変換します
self.strain_column = int(self.spinbox_strain_column.get())
self.stress_column = int(self.spinbox_stress_column.get())
self.true_strain = np.log(1 + self.data_frame.iloc[:, self.strain_column])
self.true_stress = self.data_frame.iloc[:, self.stress_column] * (1 + self.true_strain)
print(self.true_strain)
グラフの表示
plot_data()では、視覚的にわかりやすいように、変換前と変換後両方の応力ひずみ線図を表示します。
def plot_data(self):
self.ax.plot(self.true_strain, self.true_stress, label='True Stress-Strain Curve')
self.ax.plot(self.data_frame.iloc[:, self.strain_column], self.data_frame.iloc[:, self.stress_column], label='Normal Stress-Strain Curve')
self.ax.set_xlabel('True Strain')
self.ax.set_ylabel('True Stress')
self.ax.legend()
self.canvas.draw()
print("plot")
グラフ上のマウスの挙動
on_motion()では、グラフ上でマウスを動かした際に、真応力・真ひずみ線図上の最近傍点にスナップさせ、その点を赤線の十字で示し、値を軸ラベルの位置に表示しています。
nearest_point = np.argmin(np.sqrt((self.true_strain - x)**2 + (self.true_stress - y)**2))という計算で、二乗誤差が一番小さい点を最近傍点としていますが、グラフは縦横のスケールが同じではないので、変な感覚になってしまいました。
y座標が同じ近傍点にしたかったらxの部分の計算をなくせばいいですし、逆もまた然りです。
また、クリックした際は、その座標をボタンが配置してあるウィンドウのほうに表示するようになっており、on_click()で実装しています。
降伏点の取得などに役立ててください。
# クリックで座標取得
def on_click(self, event):
# マウスがクリックされた座標に最も近い点と原点を結ぶ直線の傾きを求めます
x, y = event.xdata, event.ydata
self.entry_click_pointx.delete(0, tk.END)
self.entry_click_pointx.insert(0, event.xdata)
self.entry_click_pointy.delete(0, tk.END)
self.entry_click_pointy.insert(0, event.ydata)
#カーソール位置の表示
def on_motion(self, event):
if event.xdata is not None and event.ydata is not None:
# 既存の十字線を削除
for line in self.lines:
line.remove()
self.lines.clear()
y=event.ydata
x=event.xdata
nearest_point = np.argmin(np.sqrt((self.true_strain - x)**2 + (self.true_stress - y)**2))
y = self.true_stress[nearest_point]
x = self.true_strain[nearest_point]
# 新しい十字線を描画
xline = self.ax.axhline(y=y, color='red', lw=1)
yline = self.ax.axvline(x=x, color='red', lw=1)
# 座標を更新
self.ax.set_xlabel(f'X: {event.xdata:.2f}')
self.ax.set_ylabel(f'Y: {event.ydata:.2f}')
self.lines.extend([xline, yline])
# キャンバスを更新
self.canvas.draw()
ヤング率・降伏点の視覚的描写
ヤング率を視覚的に見えるように、plot_young_modulus()を用意しています。
ボタンを押すと原点からヤング率の傾きの線が描かれます。
降伏点については、入力した降伏応力と最も値が小さい点が選ばれます。self.yield_nearest_point_index = np.argmin((self.data_frame.iloc[:, int(self.spinbox_stress_column.get())] - y)**2)
これは、公称応力ひずみ線図であらかじめ降伏点を決定している前提で作成しているからです。
ただ、降伏点は断線範囲の最後の部分であり、公称応力と真応力の差は小さいのではと考えられます。
def plot_young_modulus(self):
# ヤング率をプロットします
young_modulus = float(self.entry_young_modulus.get())
max_strain = min (max(self.true_strain), max(self.true_stress)/young_modulus)
self.ax.plot([0, max_strain], [0, young_modulus * max_strain], color="red")
self.canvas.draw()
# 元の公称応力で計算するので注意
# 降伏点と塑性データ点の計算
def set_yield_point(self):
y = float(self.entry_yield_point.get())
self.yield_nearest_point_index = np.argmin((self.data_frame.iloc[:, int(self.spinbox_stress_column.get())] - y)**2)
print(self.yield_nearest_point_index)
self.ax.plot(self.true_strain[self.yield_nearest_point_index], self.true_stress[self.yield_nearest_point_index], marker="^", label='Yield point')
self.canvas.draw()
塑性データの取得
バーを左右に動かして点数を指定し、塑性データプロットを押すと、その点数分だけ降伏応力と塑性ひずみが表示されます。
ただ。これはコピペできないようなので、print()関数でも出力しています。
def plot_plasticity_points(self):
# 降伏点から最後の点までを塑性データ点に設定します
for scatter in self.scatters:
scatter.remove()
self.scatters.clear()
young_modulus = float(self.entry_young_modulus.get())
plasticity_strains = self.true_strain - self.true_stress / young_modulus
material_values = []
material_values.append((float(self.entry_yield_point.get()), 0))
print(len(plasticity_strains))
for i in np.linspace(self.yield_nearest_point_index, len(plasticity_strains)-1, self.slider_plasticity.get(), dtype=int):
material_values.append((self.true_stress[i], plasticity_strains[i]))
scatter = self.ax.scatter(self.true_strain[i], self.true_stress[i], marker="*" )
self.scatters.append(scatter)
self.canvas.draw()
print(material_values)
self.material_df = pd.DataFrame(material_values, columns=["yield_stress", "plaxtic_strain"])
self.display_table(self.material_df, self.tree_material)
プログラム全文
プログラム全文は以下です。
# -*- coding: utf-8 -*-
import tkinter as tk
from tkinter import ttk
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
from tkinter import filedialog
class TimeSeriesDataAnalysisGUI:
def __init__(self, master):
self.master = master
master.title("引張試験 時系列データ分析")
# データ読み込みと前処理
self.data_frame = None
self.true_strain = None
self.true_stress = None
# GUI コンポーネント
self.create_graph_window(root)
#ファイル選択
self.file_path = "./test_result1.csv"
self.frame_file_path = tk.Frame(master)
self.frame_file_path.pack()
self.select_file_path_button = tk.Button(self.frame_file_path, text="ファイル選択", command=self.select_file)
self.select_file_path_button.pack(side=tk.LEFT)
self.lbl_file = tk.Label(self.frame_file_path,text=self.file_path)
self.lbl_file.pack(side=tk.LEFT)
#データ読み込み
self.frame_header = tk.Frame(master)
self.frame_header.pack()
lbl1 = tk.Label(self.frame_header,text="ヘッダーの有無:")
lbl1.pack(side=tk.LEFT)
self.spinbox_header = ttk.Spinbox(self.frame_header, values=["なし", "あり"])
self.spinbox_header.insert(tk.END,"あり")
self.spinbox_header.pack(side=tk.LEFT)
self.load_data_button = tk.Button(self.frame_header, text="データ読み込み", command=self.load_data)
self.load_data_button.pack(side=tk.LEFT)
#表で表示
self.tree = ttk.Treeview(master)
self.tree.pack()
#self.tree.pack(expand=True, fill='both')
#列の指定
self.frame_strain_column = tk.Frame(master)
self.frame_strain_column.pack()
lbl1 = tk.Label(self.frame_strain_column,text="ひずみの列(0スタート):")
lbl1.pack(side=tk.LEFT)
self.spinbox_strain_column = ttk.Spinbox(self.frame_strain_column, from_=0, to=10)
self.spinbox_strain_column.insert(tk.END,int(8))
self.spinbox_strain_column.pack(side=tk.LEFT)
self.frame_stress_column = tk.Frame(master)
self.frame_stress_column.pack()
lbl1 = tk.Label(self.frame_stress_column,text="応力の列(0スタート):")
lbl1.pack(side=tk.LEFT)
self.spinbox_stress_column = ttk.Spinbox(self.frame_stress_column, from_=0, to=10)
self.spinbox_stress_column.insert(tk.END,int(9))
self.spinbox_stress_column.pack(side=tk.LEFT)
#真ひずみに変換
self.transform_button = tk.Button(master, text="真応力-真ひずみに変換", command=self.transform_data)
self.transform_button.pack()
# データ可視化
#self.figure, self.ax = plt.subplots()
#self.canvas = FigureCanvasTkAgg(self.figure, master)
#self.canvas.get_tk_widget().pack()
self.plot_button = tk.Button(master, text="真応力-真ひずみ線図プロット", command=self.plot_data)
self.plot_button.pack()
self.canvas.get_tk_widget().pack()
self.frame_click_point = tk.Frame(master)
self.frame_click_point.pack()
lbl1 = tk.Label(self.frame_click_point,text="x:")
lbl1.pack(side=tk.LEFT)
self.entry_click_pointx = tk.Entry(self.frame_click_point)
self.entry_click_pointx.pack(side=tk.LEFT)
lbl2 = tk.Label(self.frame_click_point,text="y:")
lbl2.pack(side=tk.LEFT)
self.entry_click_pointy = tk.Entry(self.frame_click_point)
self.entry_click_pointy.pack(side=tk.LEFT)
#ヤング率取得
self.frame_young_modulus = tk.Frame(master)
self.frame_young_modulus.pack()
self.lbl1 = tk.Label(self.frame_young_modulus,text="ヤング率:")
self.lbl1.pack(side=tk.LEFT)
self.entry_young_modulus = tk.Entry(self.frame_young_modulus)
self.entry_young_modulus.pack(side=tk.LEFT)
self.entry_young_modulus.insert(tk.END,4056)
self.plot_young_modulus_button = tk.Button(self.frame_young_modulus, text="ヤング率プロット", command=self.plot_young_modulus)
self.plot_young_modulus_button.pack(side=tk.LEFT)
self.canvas.mpl_connect("button_press_event", self.on_click)
self.lines = []
self.canvas.mpl_connect('motion_notify_event', self.on_motion)
# 降伏点と塑性データ点の計算
self.frame_yield = tk.Frame(master)
self.frame_yield.pack()
lbl1 = tk.Label(self.frame_yield,text="降伏応力(公称応力):")
lbl1.pack(side=tk.LEFT)
self.entry_yield_point = tk.Entry(self.frame_yield)
self.entry_yield_point.insert(tk.END, 30)
self.entry_yield_point.pack(side=tk.LEFT)
self.change_yield_point_button = tk.Button(self.frame_yield, text="降伏点プロット", command=self.set_yield_point)
self.change_yield_point_button.pack(side=tk.LEFT)
self.slider_plasticity = tk.Scale(master, from_=0, to=100, orient="horizontal")
self.slider_plasticity.pack()
self.scatters = []
self.plot_plasticity_points_button = tk.Button(master, text="塑性データプロット", command=self.plot_plasticity_points)
self.plot_plasticity_points_button.pack()
self.tree_material = ttk.Treeview(master)
self.tree_material.pack()
# グラフを表示するウィンドウの作成
def create_graph_window(self, master):
graph_window = tk.Toplevel(master)
graph_window.title('グラフウィンドウ')
# matplotlibのFigureを作成
self.figure, self.ax = plt.subplots(figsize=(10, 8))
self.canvas = FigureCanvasTkAgg(self.figure, master=graph_window)
self.canvas.get_tk_widget().pack()
def select_file(self):
self.file_path = filedialog.askopenfilename()
self.lbl_file["text"] = self.file_path
def display_table(self, df, tree):
tree.delete(*tree.get_children())
print(df)
tree["column"] = list(df.columns)
tree["show"] = "headings"
for column in tree["column"]:
tree.heading(column, text=column)
df_rows = df.to_numpy().tolist()
for row in df_rows:
tree.insert("", "end", values=row)
# データ読み込み
def load_data(self):
# CSV ファイルをロードし、データフレームを作成します
header = self.spinbox_header.get()
print(self.file_path)
if header == "あり":
self.data_frame = pd.read_csv(self.file_path, header=0)
else:
self.data_frame = pd.read_csv(self.file_path, header=None)
self.display_table(self.data_frame, self.tree)
"""
self.tree["column"] = list(self.data_frame.columns)
self.tree["show"] = "headings"
for column in self.tree["column"]:
self.tree.heading(column, text=column)
df_rows = self.data_frame.to_numpy().tolist()
for row in df_rows:
self.tree.insert("", "end", values=row)
"""
# データ前処理
def transform_data(self):
# ひずみと応力を真値に変換します
self.strain_column = int(self.spinbox_strain_column.get())
self.stress_column = int(self.spinbox_stress_column.get())
self.true_strain = np.log(1 + self.data_frame.iloc[:, self.strain_column])
self.true_stress = self.data_frame.iloc[:, self.stress_column] * (1 + self.true_strain)
print(self.true_strain)
#グラフ表示
def plot_data(self):
self.ax.plot(self.true_strain, self.true_stress, label='True Stress-Strain Curve')
self.ax.plot(self.data_frame.iloc[:, self.strain_column], self.data_frame.iloc[:, self.stress_column], label='Normal Stress-Strain Curve')
self.ax.set_xlabel('True Strain')
self.ax.set_ylabel('True Stress')
self.ax.legend()
self.canvas.draw()
print("plot")
# クリックで座標取得
def on_click(self, event):
# マウスがクリックされた座標に最も近い点と原点を結ぶ直線の傾きを求めます
x, y = event.xdata, event.ydata
self.entry_click_pointx.delete(0, tk.END)
self.entry_click_pointx.insert(0, event.xdata)
self.entry_click_pointy.delete(0, tk.END)
self.entry_click_pointy.insert(0, event.ydata)
#カーソール位置の表示
def on_motion(self, event):
if event.xdata is not None and event.ydata is not None:
# 既存の十字線を削除
for line in self.lines:
line.remove()
self.lines.clear()
y=event.ydata
x=event.xdata
nearest_point = np.argmin(np.sqrt((self.true_strain - x)**2 + (self.true_stress - y)**2))
y = self.true_stress[nearest_point]
x = self.true_strain[nearest_point]
# 新しい十字線を描画
xline = self.ax.axhline(y=y, color='red', lw=1)
yline = self.ax.axvline(x=x, color='red', lw=1)
# 座標を更新
self.ax.set_xlabel(f'X: {event.xdata:.2f}')
self.ax.set_ylabel(f'Y: {event.ydata:.2f}')
self.lines.extend([xline, yline])
# キャンバスを更新
self.canvas.draw()
def plot_young_modulus(self):
# ヤング率をプロットします
young_modulus = float(self.entry_young_modulus.get())
max_strain = min (max(self.true_strain), max(self.true_stress)/young_modulus)
self.ax.plot([0, max_strain], [0, young_modulus * max_strain], color="red")
self.canvas.draw()
# 元の公称応力で計算するので注意
# 降伏点と塑性データ点の計算
def set_yield_point(self):
y = float(self.entry_yield_point.get())
self.yield_nearest_point_index = np.argmin((self.data_frame.iloc[:, int(self.spinbox_stress_column.get())] - y)**2)
print(self.yield_nearest_point_index)
self.ax.plot(self.true_strain[self.yield_nearest_point_index], self.true_stress[self.yield_nearest_point_index], marker="^", label='Yield point')
self.canvas.draw()
def plot_plasticity_points(self):
# 降伏点から最後の点までを塑性データ点に設定します
for scatter in self.scatters:
scatter.remove()
self.scatters.clear()
young_modulus = float(self.entry_young_modulus.get())
plasticity_strains = self.true_strain - self.true_stress / young_modulus
material_values = []
material_values.append((float(self.entry_yield_point.get()), 0))
print(len(plasticity_strains))
for i in np.linspace(self.yield_nearest_point_index, len(plasticity_strains)-1, self.slider_plasticity.get(), dtype=int):
material_values.append((self.true_stress[i], plasticity_strains[i]))
scatter = self.ax.scatter(self.true_strain[i], self.true_stress[i], marker="*" )
self.scatters.append(scatter)
self.canvas.draw()
print(material_values)
self.material_df = pd.DataFrame(material_values, columns=["yield_stress", "plaxtic_strain"])
self.display_table(self.material_df, self.tree_material)
if __name__ == "__main__":
root = tk.Tk()
app = TimeSeriesDataAnalysisGUI(root)
root.mainloop()
最後に
今回は材料試験データから降伏応力と塑性ひずみの組を取得するGUIアプリを作りました。
自分でプログラムを作ると大変ですが、中身がよくわかるほか、追加したい機能を簡単に追加できるので非常に便利です。
なおかつ今回は生成AIにベースを書いてもらったので、特に関数名や変数名、全体の流れなどが非常にきれいに作れました。
今後も生成AIはうまく使っていきたいと思います。