はじめに
この記事では、数値積分の方法の一つである、ガウス・ルジャンドル数値積分について解説していきます。
ガウス・ルジャンドル数値積分は以下の式で表され、なんと足し合わせるnに対して、2n-1次多項式の積分を厳密に計算することができます。
\begin{equation}
\int_{-1}^1 f(x)\,dx = \sum_{i=1}^n w_i f(x_i)
\end{equation}
ガウス・ルジャンドル数値積分についていろいろ調べてもわかりにくく、そして直感的でなかったため、この記事ではできるだけ式変形を丁寧に、そして図を多めに使用して解説していこうと思います。
どこで使うの?
有限要素法では、2次元で厚さが一定の要素では、以下の積分をしなければいけません。
\begin{equation}
[\boldsymbol{k}]=h\iint[\boldsymbol{B}]^T[\boldsymbol{D_e}][\boldsymbol{B}]dA \text{(要素剛性行列)}
\end{equation}
しかし、数値解析の分野では高校数学や大学の微積のように解析的に積分をすることはありません。
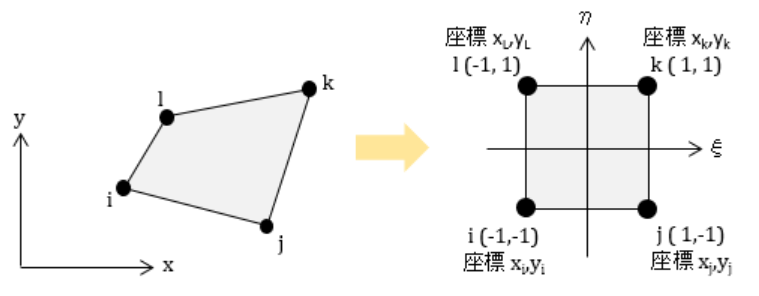
特に、有限要素法のアイソパラメトリック要素では、ガウス・ルジャンドル数値積分を使用します。
\begin{align}
[\boldsymbol{k}] &=h\iint[\boldsymbol{B}]^T[\boldsymbol{D_e}][\boldsymbol{B}]dA \text{(要素剛性行列)}\\
&= h\sum_{i=1}^n \sum_{j=1}^n w_i w_j [\boldsymbol{B}]^T[\boldsymbol{D_e}][\boldsymbol{B}] det(\boldsymbol{J}(\xi_i,\eta_j)) \\
\end{align}
用語
ガウス・ルジャンドル数値積分
今までずっとガウス・ルジャンドル数値積分という呼び方をしてきましたが、調べてみるとどうも名前がいろいろ使われています。
- ガウス求積
- ガウスの数値積分公式
- ガウスの数値積分法
- ガウス・ルジャンドル (Gauss-Legendre) の数値積分公式
- ルジャンドル・ガウスの積分公式
- ガウス・ルジャンドルの数値積分公式
- Gaussian quadrature
以後ガウス・ルジャンドル数値積分はwikiの名前に従って、ガウス求積と呼ぶことにします
積分点
以降、$x_i$を表す言葉として、積分点という言葉が出てきます。
しかしこちらも色々呼び方があり、
- ガウス点
- ガウスノード
- Gauss node
などがありますが、積分点で統一します。
ほかの積分方法
世の中にはたくさんの数値積分の方法があります。
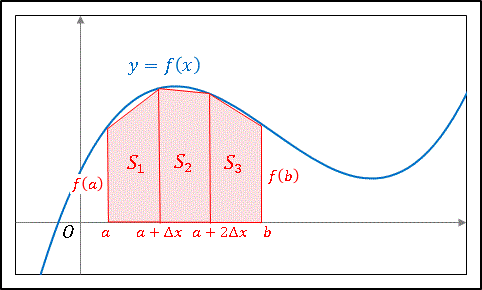
一番簡単なのは台形公式でしょうか。
以下の画像のように、求めたい関数を分割して、台形に近似して足すことで定積分を計算します。
\begin{equation}
\int_{a}^{b}f(x)dx\simeq S_1+S_2+S_3
\end{equation}
他にもたくさんの方法がありますが、すべて解説しているときりがないので、いろいろ解説しているページをいかに張っておきます。
ガウス求積
今回解説するガウス求積は以下の式で表されます。
\begin{equation}
\int_{-1}^1 f(x)\,dx \approx \sum_{i=1}^n w_i f(x_i)
\end{equation}
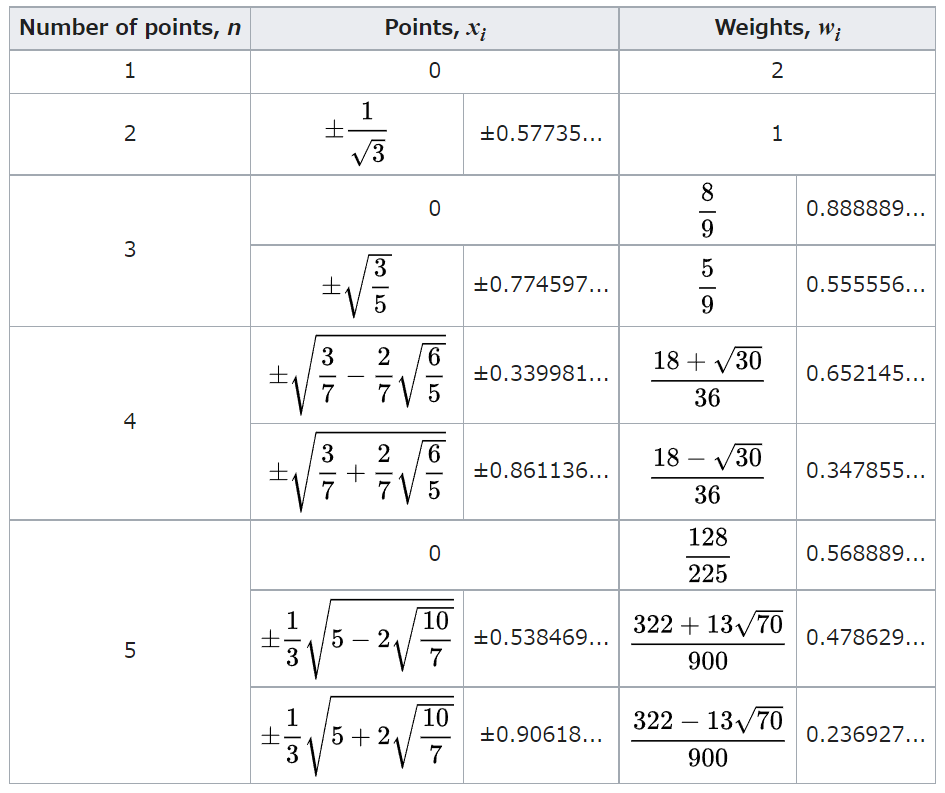
$[-1,1]$における関数$f(x)$の積分値は、後ほど解説する積分点 or ガウス点 or Gauss node) と呼ばれる、指定された$x_i$における関数の値に、対応した指定された厚み $w_i$を掛け合わせたものをn個足し合わせることで計算できます。
積分点x、厚みwの組は使用するnの値によって与えられ、以下のようになります。
n>5に関しては、wikiをご覧ください。
そして重要な性質として、ガウス求積では選んだnに対して、2n-1次以下の多項式については正確な積分値を計算することができます。
\begin{equation}
\int_{-1}^1 f(x)\,dx = \sum_{i=1}^n w_i f(x_i)
\end{equation}
ガウス求積のイメージ
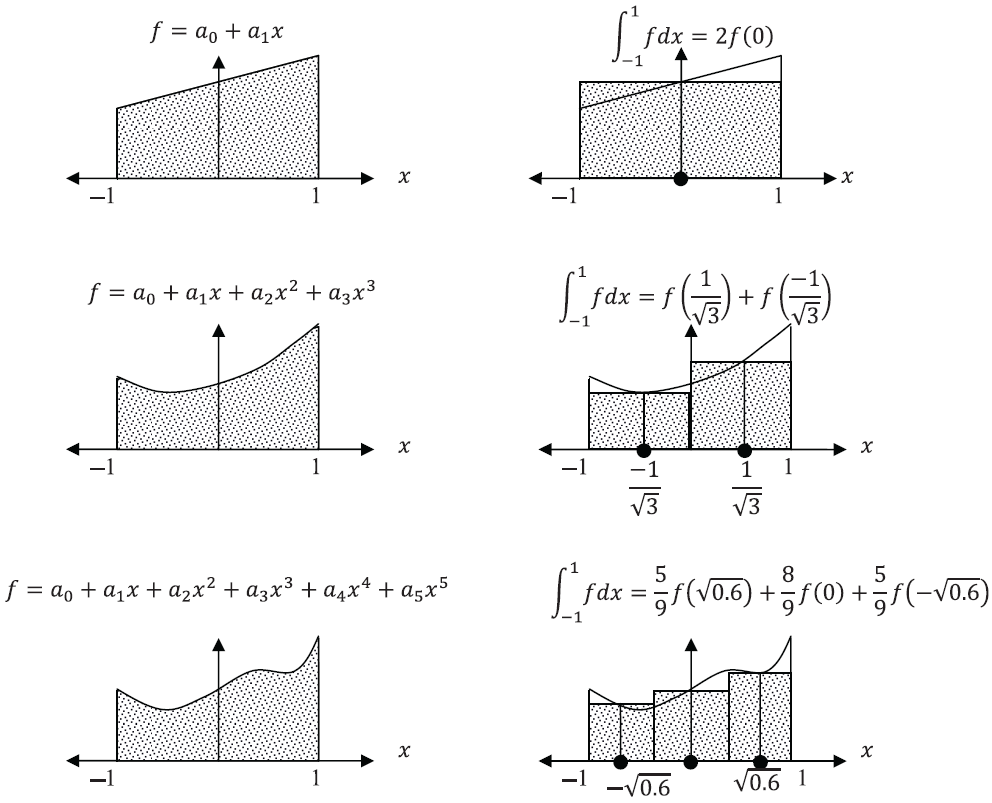
ガウス求積を可視化したものは以下です。
ある特定の積分点における関数値を高さに、対応した特定の厚みを幅として長方形要素の足し合わせで積分をしていると考えることができます。
画像出典 https://engcourses-uofa.ca/books/numericalanalysis/numerical-integration/gauss-quadrature/
導出
数式をこねくり回して変形していくのは嫌いで、本当は導出したくないですが、解説のためにしておきます。
n=1の時
n=1の時、2n-1=1次多項式以下の関数の積分値は正確に計算することができます。
答えから見ると、ガウス求積を見ると積分点はx=0、厚みはw=2なので以下のように表すことができます。
\int_{-1}^1 f(x)\,dx = 2 f(0)
1次多項式を使って、積分点x=0、厚みw=2を導きましょう。
1次関数$ax + b$を解析的に積分したものとガウス求積を使用して計算したものは、以下のように書けます。
ここで、a,bはパラメーター、x,wが未知数です。
\begin{align}
\int_{-1}^1 (ax + b) dx &= 2b\\
\sum_{i=1}^1 w_i f(x_i) &= w_1(ax_1 + b)=w_1x_1a + w_1b\\
\end{align}
以上からこのようなa,bに関する恒等式が成り立ちます。
\begin{align}
2b &= w_1x_1a + w_1b
\end{align}
よって任意のa,bについて成り立たせるために(すべての1次関数について成り立つため)、積分点は0、厚みは2が得られます。
\begin{align}
w_1 &= 2\\
x_1 &= 0
\end{align}
n=2の時
n=2の時、2n-1=3次多項式以下の関数の積分値は正確に計算することができます。
答えから見ると、ガウス求積を見ると積分点は$x=\pm\frac{1}{\sqrt{3}}$、厚みはw=1なので以下のようにあらわすことができます。
\begin{equation}
\int_{-1}^1 f(x)\,dx = 1f(\frac{-1}{\sqrt{3}}) + 1f(\frac{1}{\sqrt{3}})
\end{equation}
3次多項式を使って積分点$x=\pm\frac{1}{\sqrt{3}}$、厚みw=1を求めていきましょう。
3次関数を解析的に積分したものとガウス求積を使用して計算したものは、以下のように書けます。
ここで、$a_i$はパラメーター、$x_1, x_2, w_1, w_2$が未知数です。
\begin{align}
\int_{-1}^1 (a_0 + a_1x + a_2x^2 + a_3x^3) dx &=2a_0 + \frac{2}{3}a_2\\
\sum_{i=1}^2 w_i f(x_i) &=w_1(a_0+a_1x_1+a_2x_1^2+a_3x_1^3)+w_2(a_0+a_1x_2+a_2x_2^2+a_3x_2^3)\\
\end{align}
以上から係数を比較して、このような式が成り立ちます。
\begin{align}
a_0(w_1+w_2) + a_1(w_1x_1+w_2x_2) + a_2(w_1x_1^2+w_2x_2^2) + a_3(w_1x_1^3+w_2x_2^3) =2a_0 + \frac{2}{3}a_2
\end{align}
見やすくすると、
\begin{alignat}{2}
(w_1+w_2)&a_0 + (w_1x_1+w_2x_2)a_1& + (w_1x_1^2+w_2x_2^2)&a_2 + (w_1x_1^3+w_2x_2^3)a_3 \\
=2&a_0 &+ \frac{2}{3}&a_2
\end{alignat}
これは任意の$a_i$に対して成り立つ恒等式でなければいけないので、(すべての3次関数に対応する積分点と厚みが欲しいから)以下の式が成り立ちます。
\begin{align}
w_1 + w_2 &= 2\\
w_1x_1 + w_2x_2& = 0\\
w_1x_1^2+w_2x_2^2& = \frac{2}{3}\\
w_1x_1^3+w_2x_2^3& = 0
\end{align}
この連立方程式を解くと、
\begin{align}
x_1=\frac{-1}{\sqrt{3}} \quad w_1=1\\
x_2=\frac{+1}{\sqrt{3}} \quad w_2=1
\end{align}
という積分点と厚みの組が求まります。
n=3以上
導出方法は以下のサイトを参考にしています。n=3以上についても解説があります。
応用:任意範囲の定積分
ガウス求積は以下の式で表されます。つまり$[-1,1]$でしか積分できない使いづらい式なのでしょうか。
\begin{equation}
\int_{-1}^1 f(x)\,dx \approx \sum_{i=1}^n w_i f(x_i)
\end{equation}
いいえそれは違います。
高校性の時に習った置換積分を思い出してください。
\int_{a}^{b}f(x)\,dx=\int_{\alpha}^{\beta}f(g(t))g'(t)\,dt\\
x = g(t), g(\alpha) = a, g(\beta) = b
積分区間が$[-1,1]$、つまり$\alpha=-1,\beta=1$となるように置換積分してやれば計算することができます。
\int_a^b f(x)dx=\frac{b-a}{2}\int_{-1}^{1}f(\frac{b-a}{2}t+\frac{a+b}{2}) dt\\
t=\frac{b+a}{b-a} +\frac{2}{b-a}x
(置換後の関数の変数に積分点を代入することに注意)
応用:重積分、三重積分
今までの話は1変数の積分でした。
しかし、大学の微積で習う重積分、三重積分はどのようにすればいいのでしょうか。
結論から言うと、以下のような式になります。
\begin{align}
&\int_{-1}^1 f(x)\,dx = \sum_{i=1}^n w_i f(x_i)\\
&\int_{-1}^1 \int_{-1}^1 f(x,y)\,dxdy = \sum_{i=1}^n \sum_{j=1}^n w_i w_j f(x_i, y_j)\\
&\int_{-1}^1 \int_{-1}^1 \int_{-1}^1 f(x,y,z)\,dxdydz = \sum_{i=1}^n \sum_{j=1}^n \sum_{k=1}^n w_i w_j w_k f(x_i, y_j, z_k)
\end{align}
これらについて、導出します。
簡単な式変形であることがわかります。
重積分
\begin{align}
\int_{-1}^1 \int_{-1}^1 f(x,y)\,dxdy &= \int_{-1}^1 \{ \int_{-1}^1 f(x,y)\,dx \} dy \\
&= \int_{-1}^1 \{\sum_{i=1}^n w_i f(x_i, y) \}dy \\
&= \sum_{i=1}^n w_i \int_{-1}^1 f(x_i, y)dy \\
&= \sum_{i=1}^n w_i \{ \sum_{j=1}^n w_j f(x_i, y_j)\} \\
&= \sum_{i=1}^n \sum_{j=1}^n w_i w_j f(x_i, y_j)\\
\end{align}
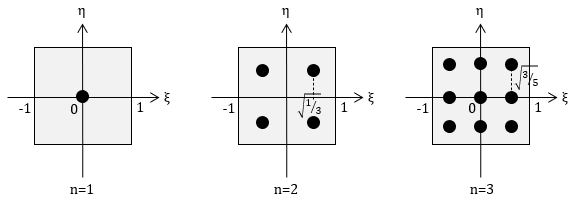
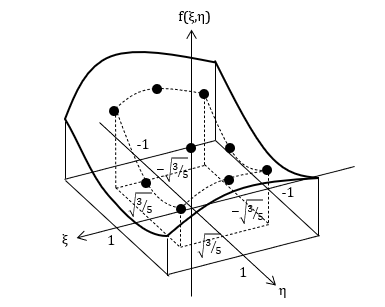
視覚的に見ると、以下のようになります。(xとξ、yとηが対応しています。)
点の座標は、各積分点のすべての組み合わせで表すことができます。
さらに、f(x,y)を高さ方向に取った3次元空間でのイメージは以下のようになります。
(xとξ、yとηが対応しています。)
これを使って重積分のガウス求積を説明すると、
ある積分点の組み合わせの座標における関数の値を高さに、積分点に対応する厚みをそれぞれ幅、奥行きとして体積を計算して足し合わせる。
と説明できます。
三重積分
三重積分についても重積分と同様です。
特に画像は用意できませんでしたが、積分点の組み合わせを三次元座標として、各厚み3つを掛け合わせて計算できます。
\begin{align}
\int_{-1}^1 \int_{-1}^1 \int_{-1}^1 f(x,y,z)\,dxdydz &= \int_{-1}^1 \int_{-1}^1 \{\sum_{i=1}^n w_i f(x_i, y,z) \}dydz \\
&= \sum_{i=1}^n w_i \int_{-1}^1 \{ \int_{-1}^1 f(x_i, y, z)dy \} dz \\
&= \sum_{i=1}^n w_i \int_{-1}^1 \{ \sum_{j=1}^n w_j f(x_i, y_j, z)\}dz \\
&= \sum_{i=1}^n \sum_{j=1}^n w_i w_j \int_{-1}^1 f(x_i, y_j,z)dz\\
&= \sum_{i=1}^n \sum_{j=1}^n w_i w_j \{ w_k \sum_{k=1}^n f(x_i, y_j,z_k) \}\\
&= \sum_{i=1}^n \sum_{j=1}^n \sum_{k=1}^n w_i w_j w_k f(x_i, y_j, z_k)
\end{align}
応用の応用:任意範囲の重積分・三重積分
任意範囲のガウス求積、$[-1,1]$の重積分、三重積分がわかったので、今度は任意範囲の重積分、三重積分をしたいのですが、どうすればいいでしょうか。
大学の微積で習った変数変換とヤコビアンを思い出しましょう。
今回の目的は、任意範囲の関数を重積分では$[-1,1]\times[-1,1]$の領域に、3重積分では$[-1,1]\times[-1,1]\times[-1,1]$の領域に変換(写像)することです。
順番に見ていきましょう。
重積分
物理座標で任意範囲をとる関数が$\hat{F}(x,y)$で表されるとき、変数変換によって自然座標$[-1,1]\times[-1,1]$の$F(\xi, \eta)$に変換(写像)されたとします。
つまり数式では以下のようになったとします。
\begin{equation}
\hat{F}(x,y) = F(x(\xi, \eta), y(\xi, \eta)) = F(\xi, \eta)
\end{equation}
この時、ヤコビ行列は以下のように表されます。
\begin{equation}
\boldsymbol{J}(\xi, \eta) =
\frac{\partial (x,y)}{\partial (\xi, \eta)} =
\begin{Bmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} \\
\frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} \\
\end{Bmatrix}
\end{equation}
そして、ヤコビアン(Jacobian)、ヤコビの行列式は以下のようになります。
\begin{equation}
det(\boldsymbol{J}(\xi, \eta)) =
\begin{vmatrix}
\frac{\partial (x,y)}{\partial (\xi, \eta)}
\end{vmatrix} = det
\begin{Bmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} \\
\frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} \\
\end{Bmatrix}
\end{equation}
ここで、ヤコビ行列、ヤコビアン、ヤコビの行列式は$(\xi, \eta)$の関数であり、定数でないことに注意。
そして重積分については、以下の式が成り立ちます。
\begin{align}
\iint \hat{F}(x,y)\,dxdy
&= \int_{-1}^1 \int_{-1}^1 F(\xi,\eta)
det(\boldsymbol{J}(\xi,\eta))
d \xi d \eta \\
&= \sum_{i=1}^n \sum_{j=1}^n w_i w_j F(\xi_i, \eta_j) det(\boldsymbol{J}(\xi_i,\eta_j)) \\
\end{align}
ここで、ヤコビアン、ヤコビの行列式は$(\xi, \eta)$の関数であり、定数でないことに注意。
これで任範囲の重積分も、ヤコビアンをかけるだけでガウス求積で求めることができました。
三重積分
三重積分についても、重積分と同じです。
物理座標で任意範囲をとる関数が$\hat{F}(x,y,z)$で表されるとき、変数変換によって自然座標$[-1,1]\times[-1,1]\times[-1,1]$の$F(\xi, \eta, \zeta)$に変換(写像)されたとします。
つまり数式では以下のようになったとします。
\begin{equation}
\hat{F}(x,y, z) = F(x(\xi, \eta, \zeta), y(\xi, \eta, \zeta), z(\xi, \eta, \zeta)) = F(\xi, \eta, \zeta)
\end{equation}
この時、ヤコビ行列は以下のように表されます。
\begin{equation}
\boldsymbol{J}(\xi, \eta, \zeta) =
\frac{\partial (x,y,z)}{\partial (\xi, \eta, \zeta)} =
\begin{Bmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} & \frac{\partial x}{\partial \zeta} \\
\frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} & \frac{\partial y}{\partial \zeta} \\
\frac{\partial z}{\partial \xi} & \frac{\partial z}{\partial \eta} & \frac{\partial z}{\partial \zeta} \\
\end{Bmatrix}
\end{equation}
そして、ヤコビアン(Jacobian)、ヤコビの行列式は以下のようになります。
\begin{equation}
det(\boldsymbol{J}(\xi, \eta, \zeta)) =
\begin{vmatrix}
\frac{\partial (x,y,z)}{\partial (\xi, \eta, \zeta)}
\end{vmatrix} = det
\begin{Bmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} & \frac{\partial x}{\partial \zeta} \\
\frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} & \frac{\partial y}{\partial \zeta} \\
\frac{\partial z}{\partial \xi} & \frac{\partial z}{\partial \eta} & \frac{\partial z}{\partial \zeta} \\
\end{Bmatrix}
\end{equation}
ここで、ヤコビ行列、ヤコビアン、ヤコビの行列式は$(\xi, \eta, \zeta)$の関数であり、定数でないことに注意。
そして重積分については、以下の式が成り立ちます。
\begin{align}
\iiint \hat{F}(x,y,z)\,dxdydz
&= \int_{-1}^1 \int_{-1}^1 \int_{-1}^1 F(\xi,\eta, \zeta)
det(\boldsymbol{J}(\xi,\eta, \zeta))
d \xi d \eta d \zeta\\
&= \sum_{i=1}^n \sum_{j=1}^n \sum_{k=1}^n w_i w_j w_k F(\xi_i,\eta_j, \zeta_k) det(\boldsymbol{J}(\xi_i,\eta_j, \zeta_k)) \\
\end{align}
ここで、ヤコビアン、ヤコビの行列式は$(\xi, \eta, \zeta)$の関数であり、定数でないことに注意。
これで任範囲の三重積分も、ヤコビアンをかけるだけでガウス求積で求めることができました。
まとめ
ガウス求積の考え方、実際に使う応用について解説しました、
私自身理解するのに時間がかかり、さらにネット上で日本語で解説しているサイトも少なく、理解するのが大変でした。
特に、「CAEと強度計算の森」というサイトの有限要素法の定式化 アイソパラメトリック要素というサイトには非常に助けられ、画像も複数引用させていただきました。
ありがとうございました。
本当はアイソパラメトリック要素について記事を書く予定でしたが、ガウス求積だけで1本記事が書けてしまいました。
もし間違い、わからない点などありましたら、教えてください。
よろしくおねがいします。
参考文献
有限要素法関連の記事