有限要素法の2次元アイソパラメトリック要素の形状関数による内挿を可視化した。

はじめに

今回は、有限要素法のアイソパラメトリック要素の形状関数による内挿を可視化しました。

有限要素法について

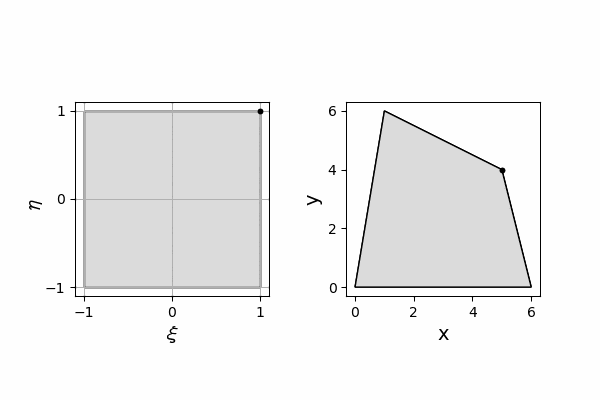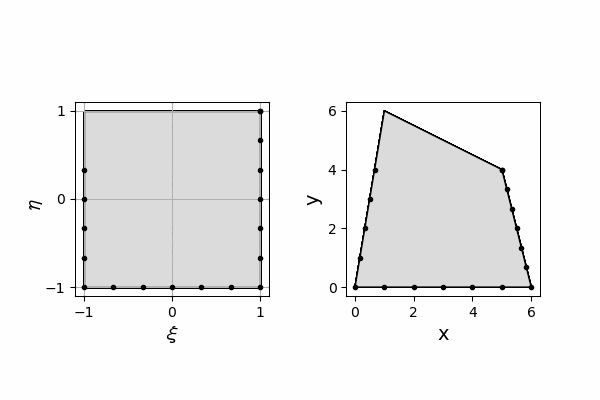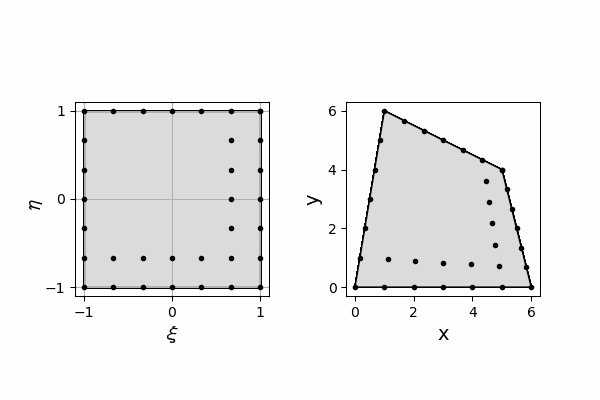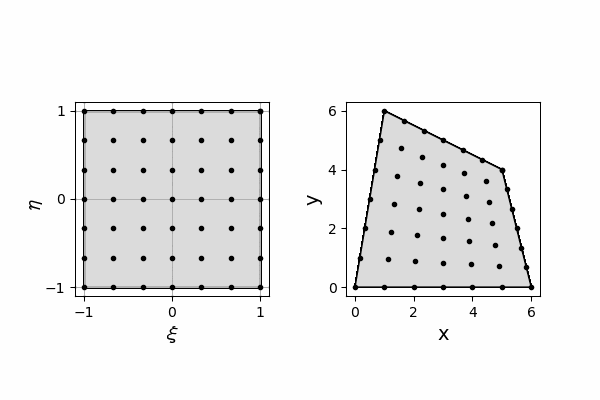
前回、以下のように有限要素法の2次元アイソパラメトリック要素の形状関数による座標変換をPythonでアニメーションにしました。

形状関数や有限要素法についての詳しい説明は、上記の記事を読んでください。

今回は、内挿も併せてアニメーションにしようと思います。

内挿とは

内挿（ないそう、英: interpolation）や補間（ほかん）とは、ある既知の数値データ列を基にして、そのデータ列の各区間の範囲内を埋める数値を求めること、またはそのような関数を与えること。またその手法を内挿法（英: interpolation method）や補間法という。対義語は外挿や補外。
https://ja.wikipedia.org/wiki/%E5%86%85%E6%8C%BF

有限要素法では、節点における値しか持ちません。
しかし、メッシュ内の要素にももちろんある値が連続的に分布しています。

アイソパラメトリック要素では、先に書いた座標変換と同じ形状関数を使用することから、アイソ(iso) つまり同じという語が付いています。

今回は、2次元4節点四角形要素の内挿を行うため、4節点の値のみ与えられており、その4つの値から要素内の任意の場所の値を推定します。

使用する形状関数は以下の通りです。

\begin{align}
N_1(\xi, \eta)=\frac{1}{4}(1-\xi)(1-\eta) \\
N_2(\xi, \eta)=\frac{1}{4}(1+\xi)(1-\eta) \\
N_3(\xi, \eta)=\frac{1}{4}(1+\xi)(1+\eta) \\
N_4(\xi, \eta)=\frac{1}{4}(1-\xi)(1+\eta)
\end{align}

そして、今回わかりやすいように要素内の温度Tをこれらの形状関数を使用して以下のように内挿します。

\begin{align}
T(\xi, \eta)=&N_1(\xi, \eta)\cdot T_1+N_2(\xi, \eta)\cdot T_2+N_3(\xi, \eta)\cdot T_3+N_4(\xi, \eta)\cdot T_4 
\end{align}

なお、温度はわかりやすいために使用しているだけで、ひずみ、変位、応力、など様々なものに応用できます。
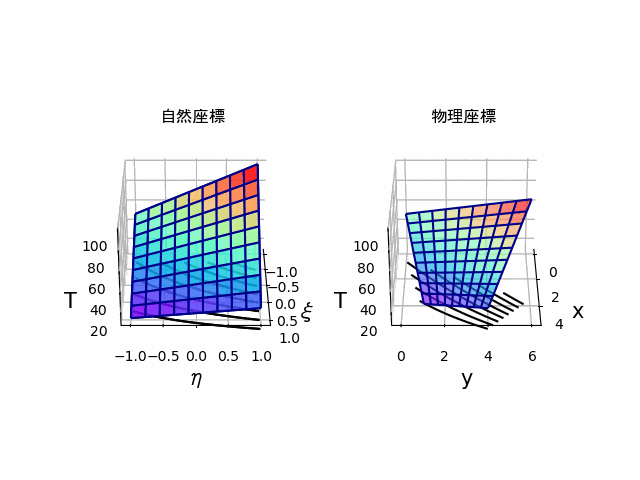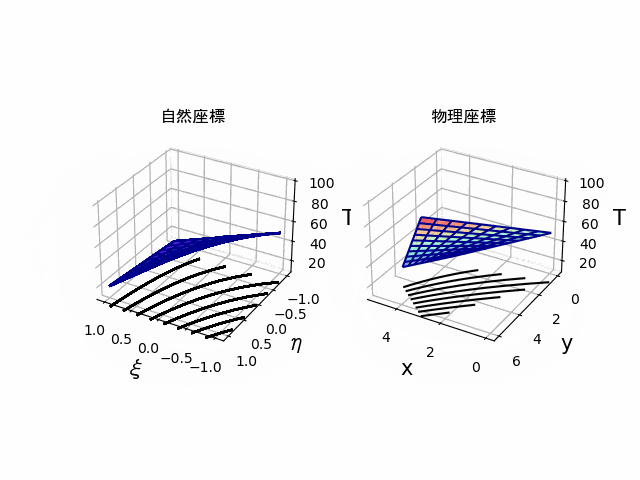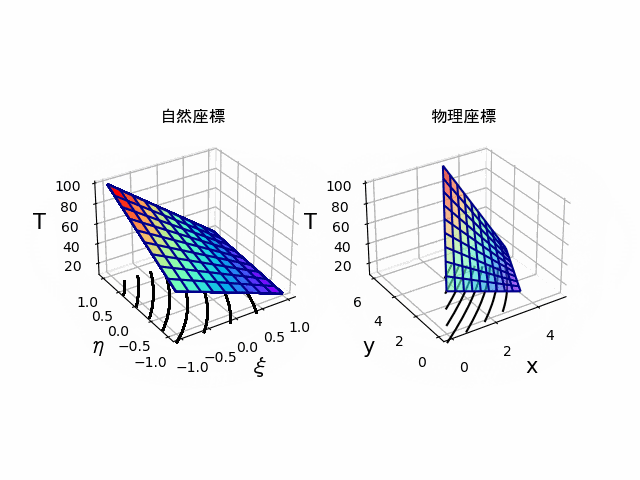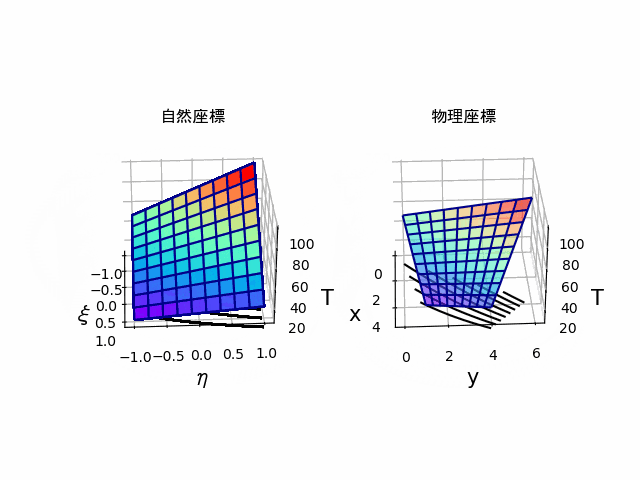
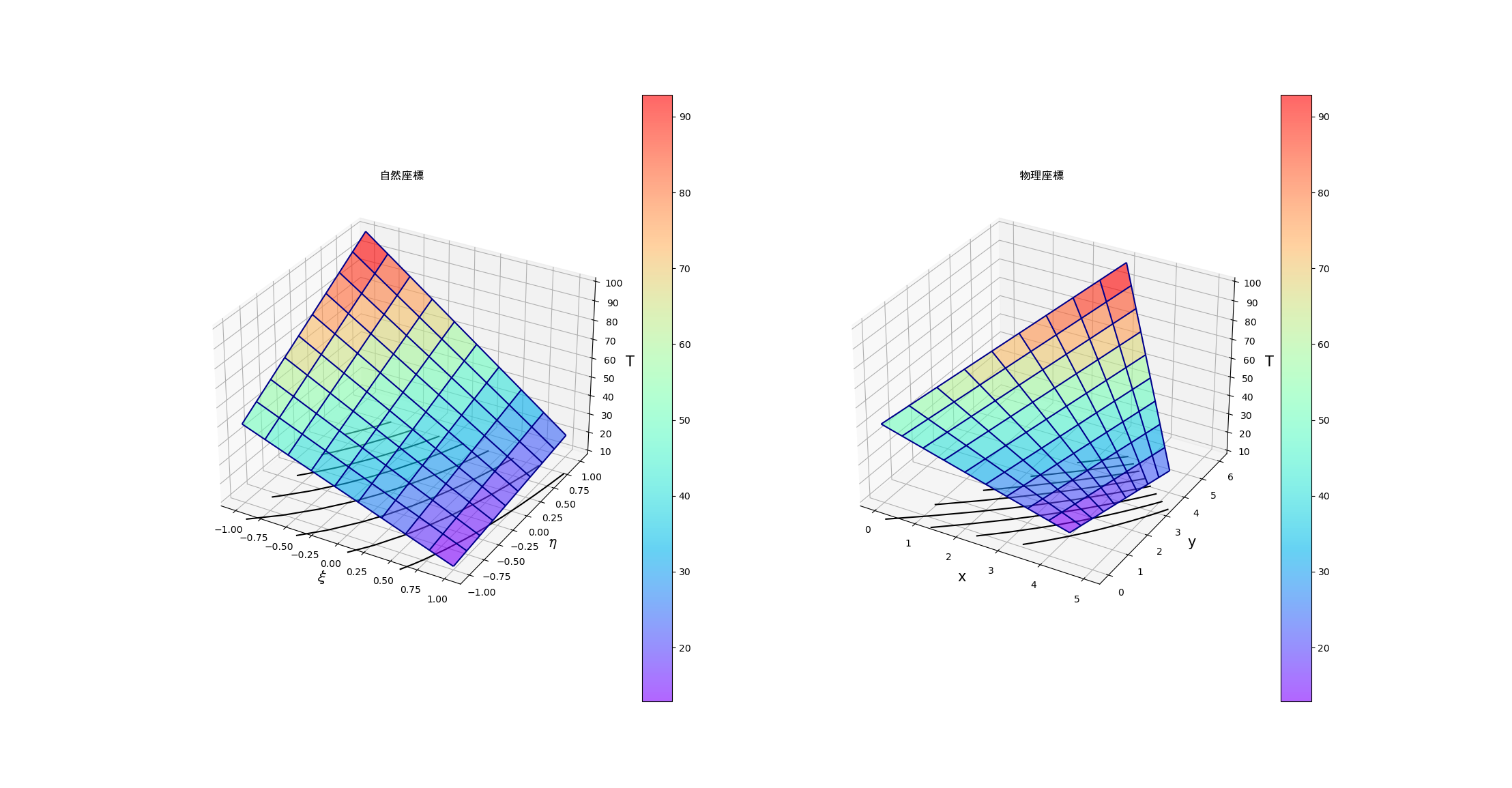
そして、プログラムでは、自然座標、物理座標における温度分布を3次元的に表します。

プログラム

今回は、matplotlibの3D描写機能、matplotlib.animationにあるFuncAnimationを使用して作成しました。

今回の描写プログラムは以下のようになっています。
入力する自然座標で四角形に等分されたメッシュでの交点の座標値$\xi, \eta$としています。
変換前の四角形の節点座標はnode_xi、node_etaに格納され、
変換後の四角形の節点座標はnode_x、node_yに格納され
節点での温度はTに格納されています。
そして、Tについて節点での値を与え、それをisox(xi, eta, x1, x2, x3, x4)関数で内挿したY_plotを自然座標、物理座標両方で表示しています。

実行するとぐりぐり動かせると思います。
もし動かせず、エディターでSpyderを使っていたら、以下のサイトを参考にしてください。

サーフェス

出来上がりがこちらです。

下に描かれている線は、等高線です。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


#各形状関数
def N1(xi, eta):
    n = (1-xi)*(1-eta)/4
    return n

def N2(xi, eta):
    n = (1+xi)*(1-eta)/4
    return n

def N3(xi, eta):
    n = (1+xi)*(1+eta)/4
    return n

def N4(xi, eta):
    n = (1-xi)*(1+eta)/4
    return n

#形状関数による自然座標から物理座標への変換
def isox(xi, eta, x1, x2, x3, x4):
    x  = x1*N1(xi, eta)
    x += x2*N2(xi, eta)
    x += x3*N3(xi, eta)
    x += x4*N4(xi, eta)    
    return x




#メッシュの密度
N = 10
xi = np.linspace(-1, 1, N)
eta = np.linspace(-1, 1, N)
xi, eta = np.meshgrid(xi, eta)


#自然座標の四角形（左下から）
node_xi =[-1,1,1,-1]
node_eta =[-1,-1,1,1]

#物理座標の四角形（左下から）
node_x = [0,4,5,3]
node_y = [0,1,4,6]

#今回内挿する変数の節点での値（左下から）
T = [50,10,20,100]




x = isox(xi, eta, *node_x)
y = isox(xi, eta, *node_y)
Y_plot = isox(xi, eta, *T)




fig = plt.figure()
ax1 = fig.add_subplot(121, projection='3d')
ax1.set_xlabel("ξ", fontname="MS Gothic",size=15,color="black")
ax1.set_ylabel("η", fontname="MS Gothic",size=15,color="black")
ax1.set_zlabel("T",size=15,color="black")

surf = ax1.plot_surface(xi, eta, Y_plot, cmap='rainbow', linewidth=0, alpha=0.6)
fig.colorbar(surf)
ax1.set_title("自然座標", fontname="MS Gothic")
#等高線
ax1.contour(xi, eta, Y_plot,colors="black",offset=-1, levels=9)
#ワイヤフレーム
ax1.plot_wireframe(xi, eta, Y_plot,color="darkblue")




ax2 = fig.add_subplot(122,projection='3d')
ax2.set_xlabel("x",size=15,color="black")
ax2.set_ylabel("y",size=15,color="black")
ax2.set_zlabel("T",size=15,color="black")

surf = ax2.plot_surface(x, y, Y_plot, cmap='rainbow', linewidth=0, alpha=0.6)
fig.colorbar(surf)
ax2.set_title("物理座標", fontname="MS Gothic")
#等高線
ax2.contour(x, y, Y_plot,colors="black",offset=-1, levels=9)
#ワイヤフレーム
ax2.plot_wireframe(x, y,Y_plot,color="darkblue")

fig.show()

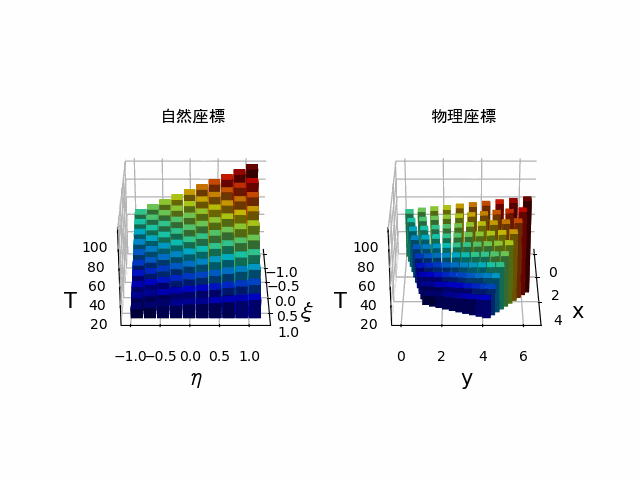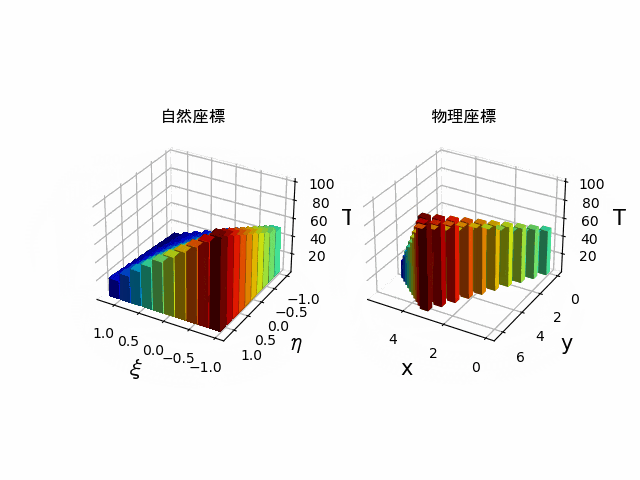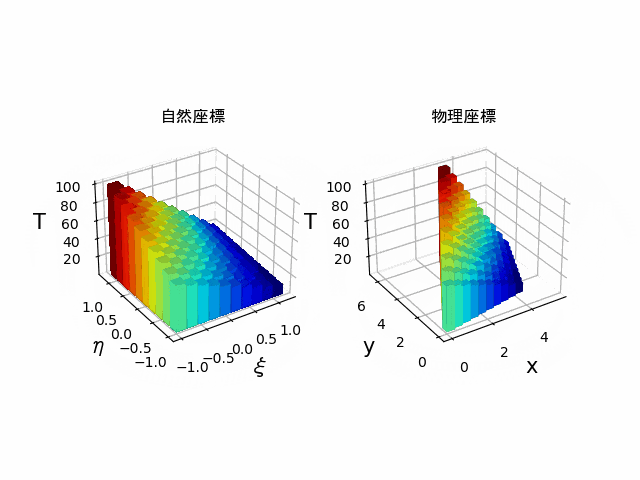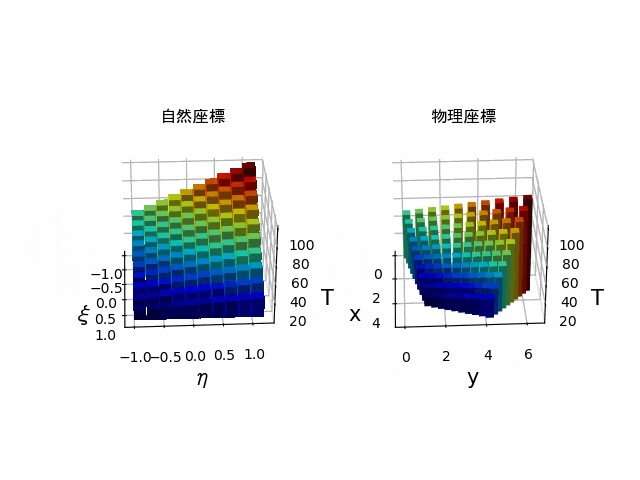
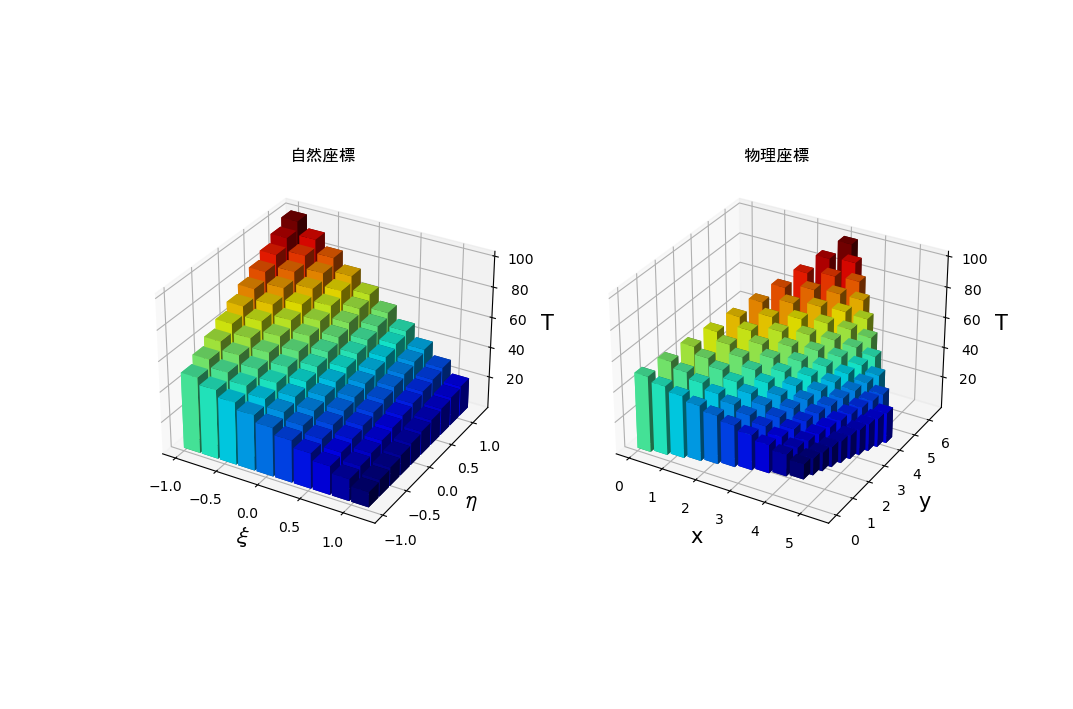
棒グラフバージョン

こちらを使って棒グラフに色を付けました

出来上がりがこちらです。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.colors as colors
import matplotlib.cm as cm


#各形状関数
def N1(xi, eta):
    n = (1-xi)*(1-eta)/4
    return n

def N2(xi, eta):
    n = (1+xi)*(1-eta)/4
    return n

def N3(xi, eta):
    n = (1+xi)*(1+eta)/4
    return n

def N4(xi, eta):
    n = (1-xi)*(1+eta)/4
    return n

#形状関数による自然座標から物理座標への変換
def isox(xi, eta, x1, x2, x3, x4):
    x  = x1*N1(xi, eta)
    x += x2*N2(xi, eta)
    x += x3*N3(xi, eta)
    x += x4*N4(xi, eta)    
    return x




#メッシュの密度
N = 10
xi = np.linspace(-1, 1, N)
eta = np.linspace(-1, 1, N)
xi, eta = np.meshgrid(xi, eta)
xi = xi.ravel()
eta = eta.ravel()



#自然座標の四角形（左下から）
node_xi =[-1,1,1,-1]
node_eta =[-1,-1,1,1]

#物理座標の四角形（左下から）
node_x = [0,4,5,3]
node_y = [0,1,4,6]

#今回内挿する変数の節点での値（左下から）
T = [50,10,20,100]




x = isox(xi, eta, *node_x)
y = isox(xi, eta, *node_y)
Y_plot = isox(xi, eta, *T)




fig = plt.figure()
ax1 = fig.add_subplot(121, projection='3d')
ax1.set_xlabel("ξ", fontname="MS Gothic",size=15,color="black")
ax1.set_ylabel("η", fontname="MS Gothic",size=15,color="black")
ax1.set_zlabel("T",size=15,color="black")



ax1.set_title("自然座標", fontname="MS Gothic")

bottom = np.ones_like(Y_plot)
width = 0.2
depth = 0.2


dz = Y_plot
offset = dz + np.abs(dz.min())
fracs = offset.astype(float)/offset.max()
norm = colors.Normalize(fracs.min(), fracs.max())
color_values = cm.jet(norm(fracs.tolist()))


ax1.bar3d(xi, eta, bottom, width, depth, Y_plot, color=color_values,alpha=1)



ax2 = fig.add_subplot(122,projection='3d')
ax2.set_xlabel("x",size=15,color="black")
ax2.set_ylabel("y",size=15,color="black")
ax2.set_zlabel("T",size=15,color="black")



ax2.set_title("物理座標", fontname="MS Gothic")


bottom = np.ones_like(Y_plot)
width = 0.4
depth = 0.4

dz = Y_plot
offset = dz + np.abs(dz.min())
fracs = offset.astype(float)/offset.max()
norm = colors.Normalize(fracs.min(), fracs.max())
color_values = cm.jet(norm(fracs.tolist()))


ax2.bar3d(x, y, bottom, width, depth, Y_plot, color=color_values,alpha=1)

fig.show()

回転アニメーション

こちらの記事を参考に回してみました
https://www.anarchive-beta.com/entry/2022/01/21/213000

サーフェスの回転アニメーション

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.colors as colors
import matplotlib.cm as cm
from matplotlib.animation import FuncAnimation


#各形状関数
def N1(xi, eta):
    n = (1-xi)*(1-eta)/4
    return n

def N2(xi, eta):
    n = (1+xi)*(1-eta)/4
    return n

def N3(xi, eta):
    n = (1+xi)*(1+eta)/4
    return n

def N4(xi, eta):
    n = (1-xi)*(1+eta)/4
    return n

#形状関数による自然座標から物理座標への変換
def isox(xi, eta, x1, x2, x3, x4):
    x  = x1*N1(xi, eta)
    x += x2*N2(xi, eta)
    x += x3*N3(xi, eta)
    x += x4*N4(xi, eta)    
    return x




#メッシュの密度
N = 10
xi = np.linspace(-1, 1, N)
eta = np.linspace(-1, 1, N)
xi, eta = np.meshgrid(xi, eta)




#自然座標の四角形（左下から）
node_xi =[-1,1,1,-1]
node_eta =[-1,-1,1,1]

#物理座標の四角形（左下から）
node_x = [0,4,5,3]
node_y = [0,1,4,6]

#今回内挿する変数の節点での値（左下から）
T = [50,10,20,100]




x = isox(xi, eta, *node_x)
y = isox(xi, eta, *node_y)
Y_plot = isox(xi, eta, *T)




# 作図用の角度を作成
v_vals = np.arange(start=-90.0, stop=270.0, step=3.0)
h_vals = np.arange(start=0.0, stop=360.0, step=3.0)



fig = plt.figure()
ax1 = fig.add_subplot(121, projection='3d')
ax2 = fig.add_subplot(122,projection='3d')


def update(i):
    print(i)
    # 前フレームのグラフを初期化
    plt.cla()
    
    # i回目の角度を取得
    #v = 0.0
    v = 30.0
    h = 270.0
    #v = v_vals[i]
    h = h_vals[i]
    
    
    
    ax1.set_xlabel("ξ", fontname="MS Gothic",size=15,color="black")
    ax1.set_ylabel("η", fontname="MS Gothic",size=15,color="black")
    ax1.set_zlabel("T",size=15,color="black")
    
    
    
    ax1.set_title("自然座標", fontname="MS Gothic")
    
    surf = ax1.plot_surface(xi, eta, Y_plot, cmap='rainbow', linewidth=0, alpha=0.6)
    #fig.colorbar(surf)
    ax1.set_title("自然座標", fontname="MS Gothic")
    #等高線
    ax1.contour(xi, eta, Y_plot,colors="black",offset=-1, levels=9)
    #ワイヤフレーム
    ax1.plot_wireframe(xi, eta, Y_plot,color="darkblue")
    
    ax1.view_init(elev=v, azim=h) # 表示アングル
    
    
    
    
    ax2.set_xlabel("x",size=15,color="black")
    ax2.set_ylabel("y",size=15,color="black")
    ax2.set_zlabel("T",size=15,color="black")
    
    
    
    ax2.set_title("物理座標", fontname="MS Gothic")
    
    
    surf = ax2.plot_surface(x, y, Y_plot, cmap='rainbow', linewidth=0, alpha=0.6)
    #fig.colorbar(surf)
    ax2.set_title("物理座標", fontname="MS Gothic")
    #等高線
    ax2.contour(x, y, Y_plot,colors="black",offset=-1, levels=9)
    #ワイヤフレーム
    ax2.plot_wireframe(x, y,Y_plot,color="darkblue")
    
    ax2.view_init(elev=v, azim=h) # 表示アングル
    





# gif画像を作成
anime_bar3d = FuncAnimation(fig, update, frames=len(v_vals), interval=100)

# gif画像を保存
anime_bar3d.save('bar3d.gif')

棒グラフの回転アニメーション

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.colors as colors
import matplotlib.cm as cm
from matplotlib.animation import FuncAnimation


#各形状関数
def N1(xi, eta):
    n = (1-xi)*(1-eta)/4
    return n

def N2(xi, eta):
    n = (1+xi)*(1-eta)/4
    return n

def N3(xi, eta):
    n = (1+xi)*(1+eta)/4
    return n

def N4(xi, eta):
    n = (1-xi)*(1+eta)/4
    return n

#形状関数による自然座標から物理座標への変換
def isox(xi, eta, x1, x2, x3, x4):
    x  = x1*N1(xi, eta)
    x += x2*N2(xi, eta)
    x += x3*N3(xi, eta)
    x += x4*N4(xi, eta)    
    return x




#メッシュの密度
N = 10
xi = np.linspace(-1, 1, N)
eta = np.linspace(-1, 1, N)
xi, eta = np.meshgrid(xi, eta)
xi = xi.ravel()
eta = eta.ravel()



#自然座標の四角形（左下から）
node_xi =[-1,1,1,-1]
node_eta =[-1,-1,1,1]

#物理座標の四角形（左下から）
node_x = [0,4,5,3]
node_y = [0,1,4,6]

#今回内挿する変数の節点での値（左下から）
T = [50,10,20,100]




x = isox(xi, eta, *node_x)
y = isox(xi, eta, *node_y)
Y_plot = isox(xi, eta, *T)




# 作図用の角度を作成
v_vals = np.arange(start=-90.0, stop=270.0, step=3.0)
h_vals = np.arange(start=0.0, stop=360.0, step=3.0)



fig = plt.figure()
ax1 = fig.add_subplot(121, projection='3d')
ax2 = fig.add_subplot(122,projection='3d')


def update(i):
    print(i)
    # 前フレームのグラフを初期化
    plt.cla()
    
    # i回目の角度を取得
    #v = 0.0
    v = 30.0
    h = 270.0
    #v = v_vals[i]
    h = h_vals[i]
    
    
    
    ax1.set_xlabel("ξ", fontname="MS Gothic",size=15,color="black")
    ax1.set_ylabel("η", fontname="MS Gothic",size=15,color="black")
    ax1.set_zlabel("T",size=15,color="black")
    
    
    
    ax1.set_title("自然座標", fontname="MS Gothic")
    
    bottom = np.ones_like(Y_plot)
    width = 0.2
    depth = 0.2
    
    
    dz = Y_plot
    offset = dz + np.abs(dz.min())
    fracs = offset.astype(float)/offset.max()
    norm = colors.Normalize(fracs.min(), fracs.max())
    color_values = cm.jet(norm(fracs.tolist()))
    
    
    ax1.bar3d(xi, eta, bottom, width, depth, Y_plot, color=color_values,alpha=1)
    
    ax1.view_init(elev=v, azim=h) # 表示アングル
    
    
    
    
    ax2.set_xlabel("x",size=15,color="black")
    ax2.set_ylabel("y",size=15,color="black")
    ax2.set_zlabel("T",size=15,color="black")
    
    
    
    ax2.set_title("物理座標", fontname="MS Gothic")
    
    
    bottom = np.ones_like(Y_plot)
    width = 0.4
    depth = 0.4
    
    dz = Y_plot
    offset = dz + np.abs(dz.min())
    fracs = offset.astype(float)/offset.max()
    norm = colors.Normalize(fracs.min(), fracs.max())
    color_values = cm.jet(norm(fracs.tolist()))
    
    
    ax2.bar3d(x, y, bottom, width, depth, Y_plot, color=color_values,alpha=1)
    
    ax2.view_init(elev=v, azim=h) # 表示アングル
    





# gif画像を作成
anime_bar3d = FuncAnimation(fig, update, frames=len(v_vals), interval=100)

# gif画像を保存
anime_bar3d.save('bar3d.gif')

まとめ

以上のように形状関数による内挿を可視化することができました。
私自身、内挿という概念がイメージしにくかったので、視覚的にみることで分かりやすくなったかと思います。

参考サイト

有限要素法関連の記事