目次
- 文系フロントエンドエンジニアは、アニメーションに三角関数をどう活用したら良いのか Part.1
- 文系フロントエンドエンジニアは、アニメーションに三角関数をどう活用したら良いのか Part.2
はじめに
三角関数を調べていて、素敵な記事を見つけました。
三角関数、何に使うの?→点を回すことができます(すごい)
タイトルの通り、上記記事の主題は**「三角関数とは、点を回す道具である」**というお話です。
前回は「y=sin(θ)やy=cos(θ)の返り値は何かと都合が良いので、アニメーションに使えるぜ!」的なお話だったのですが、
今回はその三角関数の図形的性質そのものに着目して、色々やってみようと。
視覚的理解
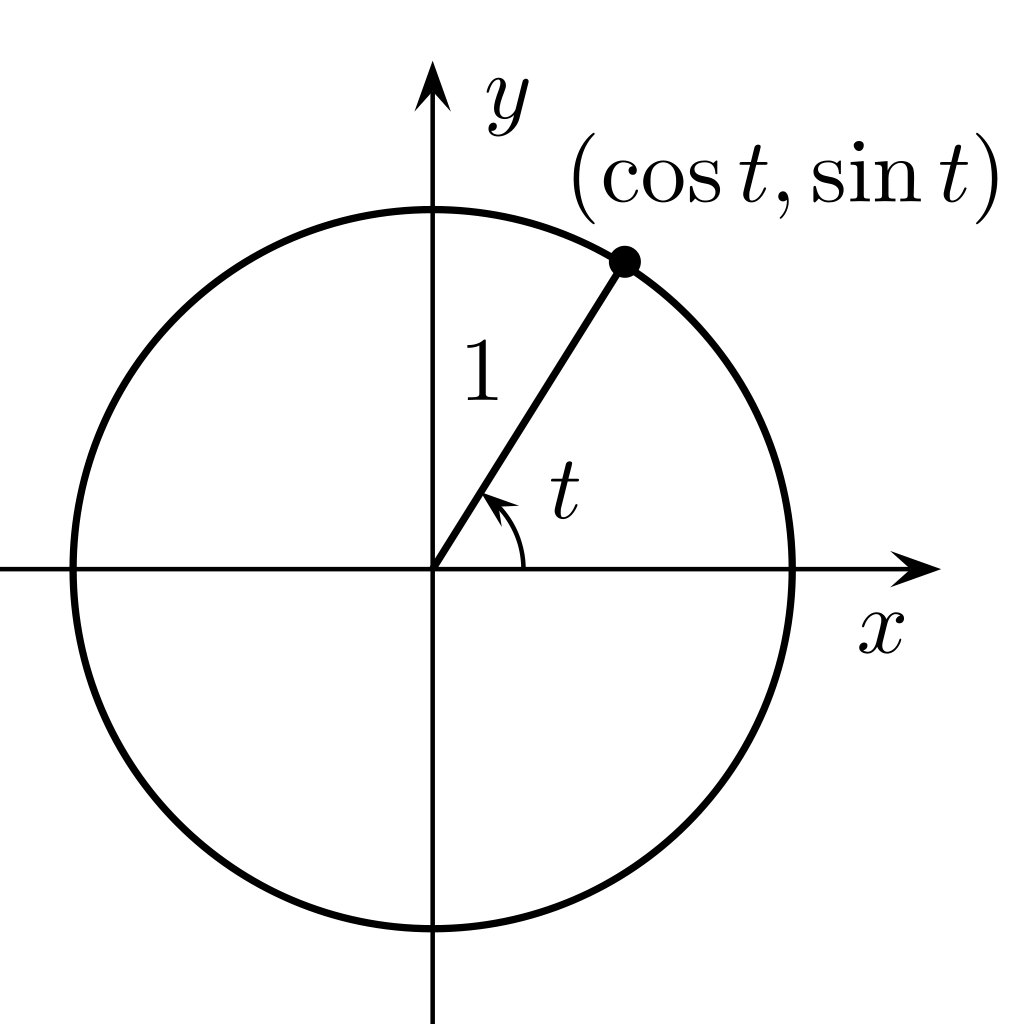
画像はwikipediaより
半径1の円を考えた時、三角関数の定義から
x座標はcosθ、y座標はsinθである。 (上記図ではθをtで表してますが)
なぜか?よくわからんけど、そういう定義である!突っ込んだら沼なのでこの辺で。
上の図の点について、θ(t)をぐにょぐにょ動かしていけば、一周して円を描きそうだ。
理屈はわからんが、性質として便利そうだ。
ということで使ってみよう。
アニメーションの大枠
簡単なのでTweenMaxで動かすことを考えます。
TweenMax.set($obj,{
x: Math.cos(θ) * 100,
y: Math.sin(θ) * 100
});
x座標がcosθ、y座標がsinθなのだから、こう設定すればいいかな。
(100を掛けているのは、sinθもcosθも-1から1の間で値を変えるためです。
そのままだとあまりにも変化幅が小さすぎるので、アニメーションがわかりやすいように100を掛けました。)
※より数学的には、半径1じゃアニメーション見えないから、半径100にしました。
θはラジアンだが、ラジアン変換公式は前回学んだ通り。
とりあえず下の関数に角度をぶちこめばいい。
function radian(val) {
return val * Math.PI / 180;
}
θを動かせば、「円を描く」ようになるけど、
θを動かすっていうのはつまり角度を動かすこと。
requestAnimationFrameで1フレームごとに角度を増やしていけばいいな。
ここも前回と変わらない!
アニメーションを書いてみた
See the Pen Trigonometric function Practice vol.2 by yuki tanabe (@yuki-tanabe-plusd) on CodePen.
リサジュー図形を描く
タイトルは理系っぽくカッコイイので書いてみました。
sin、cosで描かれる図形をリサジュー図形というらしいです。
引用記事にあったのですが、
2sin(θ)だったり、sin(2θ)にすることで、図形を拡張できるようです。
外側の掛け算 : 回転の半径
内側の掛け算 : 回転数
に影響するようで。
とりあえず色々いじってみます。
外側の掛け算
縦長になりました。
sinθに2をかけています。(2sinθ)
See the Pen リサジュー図形1 by yuki tanabe (@yuki-tanabe-plusd) on CodePen.
内側の掛け算
軌跡がわかりづらいですが、良い感じに!
sinθのθに2をかけています。sin(2θ)
See the Pen リサジュー図形2 by yuki tanabe (@yuki-tanabe-plusd) on CodePen.
最初の引用記事によると、
下記のような理解をすればよいみたいです。わかりやすい。
sinやcosの内側にかけられた数は回転数に影響します。cos(横往復)とsin(縦往復)の中身を比べると、sinだけが2倍になっているので「横に1回往復する間に縦に2回往復する」感じになっていることがお分かりいただけますでしょうか。
最後に
視覚的ではありますが、なんとなく理解ができたのと、
後半のリサジュー図形については微調整が効きそうで実践でも使えそうです。
これでwebGL学習への理論武装が整ってきました!
頑張ります。