娘に数学を教えているんですが、
問題:
$f(x) = x^2 + 2px + 3p^2-6p-36$
において、$f(x) = 0$ を満たす x が存在するとき、p の取りうる範囲を求めよ
のような問題がありました。高校の数学Iです。
これは判別式がゼロ以上となるように p の範囲を求めればよく、答えは
$-3 \leq p \leq 6$
こうなるんですが、p がこの範囲を動くときに $f(x) = 0$ が解を持つ、ってわかりにくいですね。
というか、娘にわかってもらう方法が難しい。
というわけで、Unity でグラフを描画してインタラクティブに動かしてみせるのです。
https://github.com/dsedb/math_graph
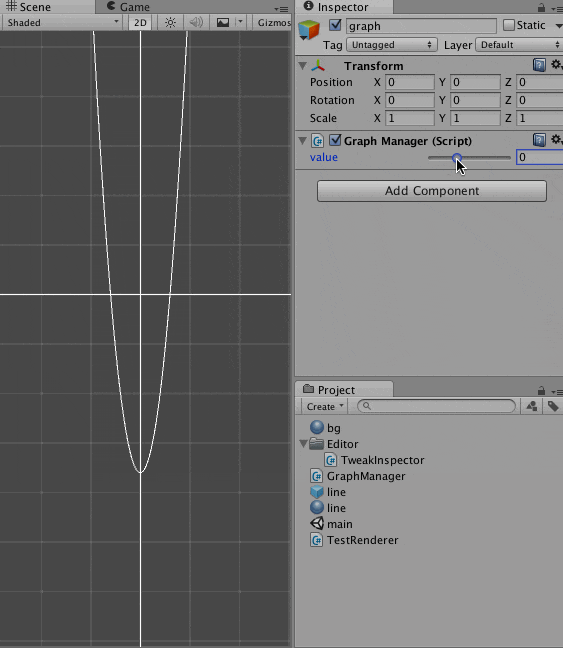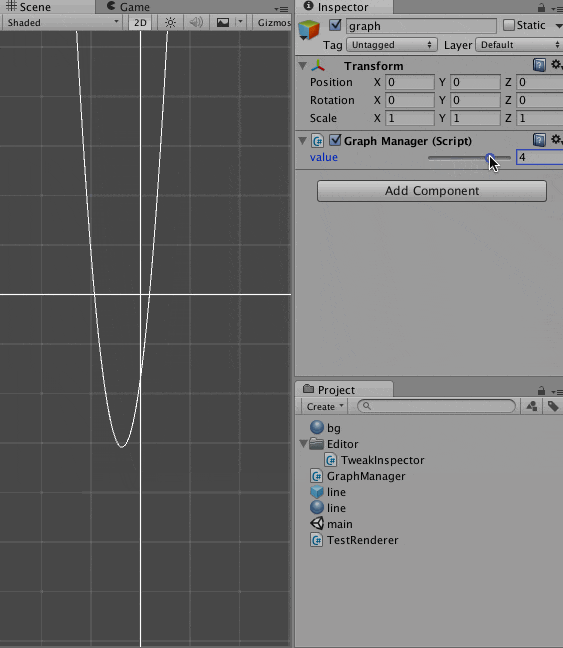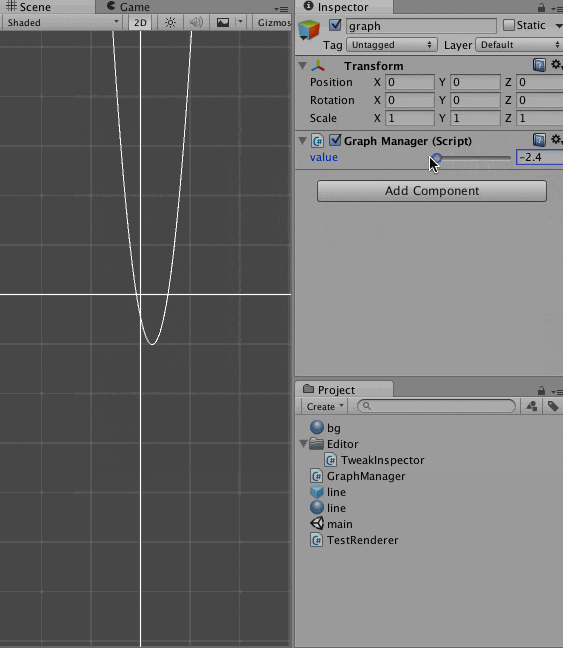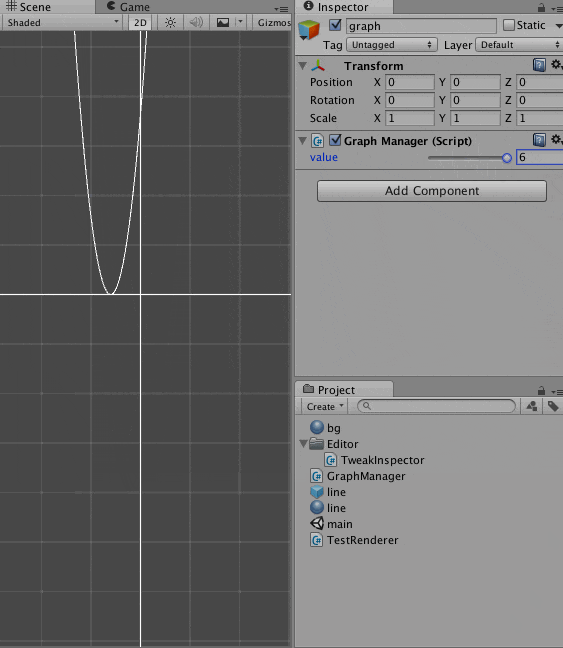
こうなります。
p の値を変更したときのグラフの変化を可視化したわけです。
スライダはエディタ拡張にしました。あと Scene ビューです。まあ、なんでもいいのです。
こうして動かしてみると、X軸と交差するのが条件、というのがわかりやすいですね。
娘「あーこうなるんだー」
少しは理解が進んだようです。めでたし。