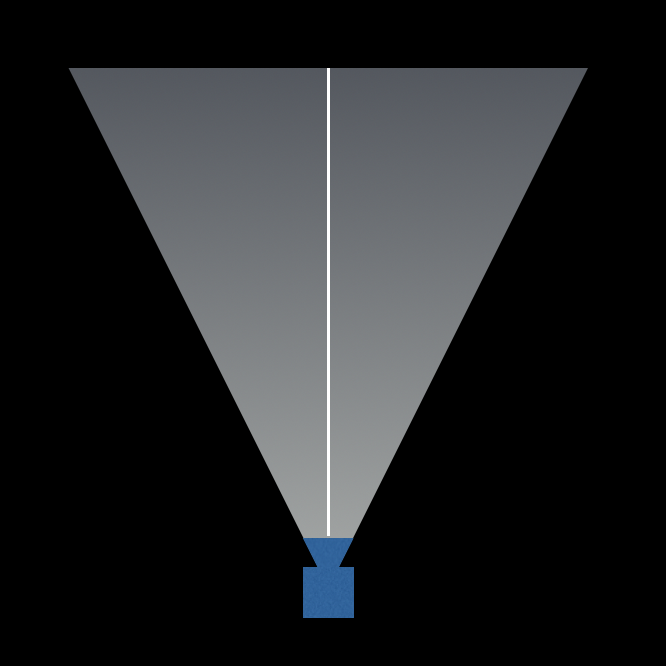
Oblique Matrix って日本語でなんて言うのだろ。まとにかく、斜めの投影行列(Oblique Projection Matrix)を使って空間を切り抜く効果を作ってみます。
まずは結果から
 © UTJ/UCL
© UTJ/UCL
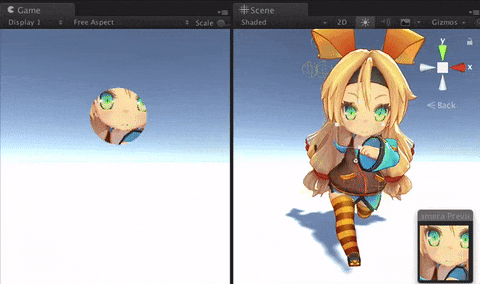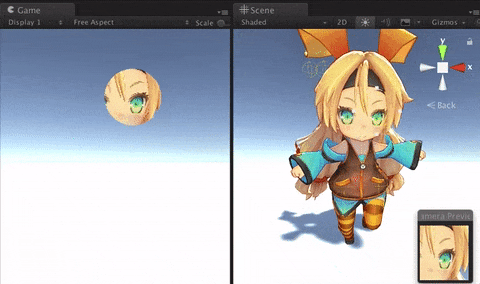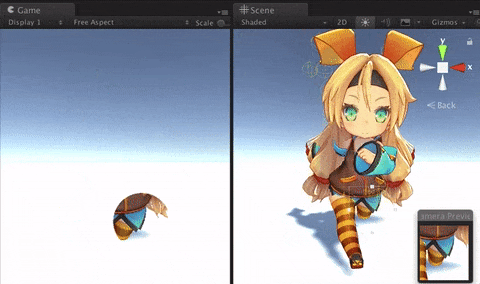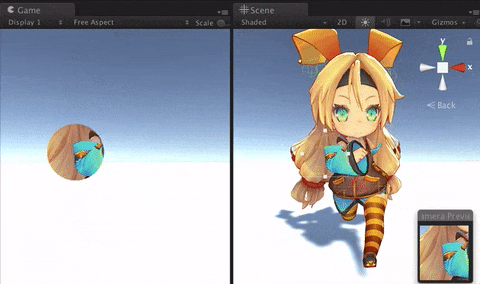
こうなります。左がゲームビュー。マウスでクリックした位置に現れる窓から、走るユニティちゃんが見えます。右はシーンビュー。カメラが一部分だけ描画しているのがわかるでしょうか。
全画面は描画しない
注目したいのは、ユニティちゃんのいる空間の全画面は描画していない、というところですね。窓から見える空間だけを描画することで、処理負荷を最低限に抑えることができます。もしこれをステンシルでやると、全画面ぶん描画しないといけなくなります。これはたいへんな無駄で、CPUやGPUを悲しませてしまいます。
Oblique Projection Matrix 〜斜めの投影行列〜
窓の部分だけを描画するためには、斜めの投影行列が必要になります。
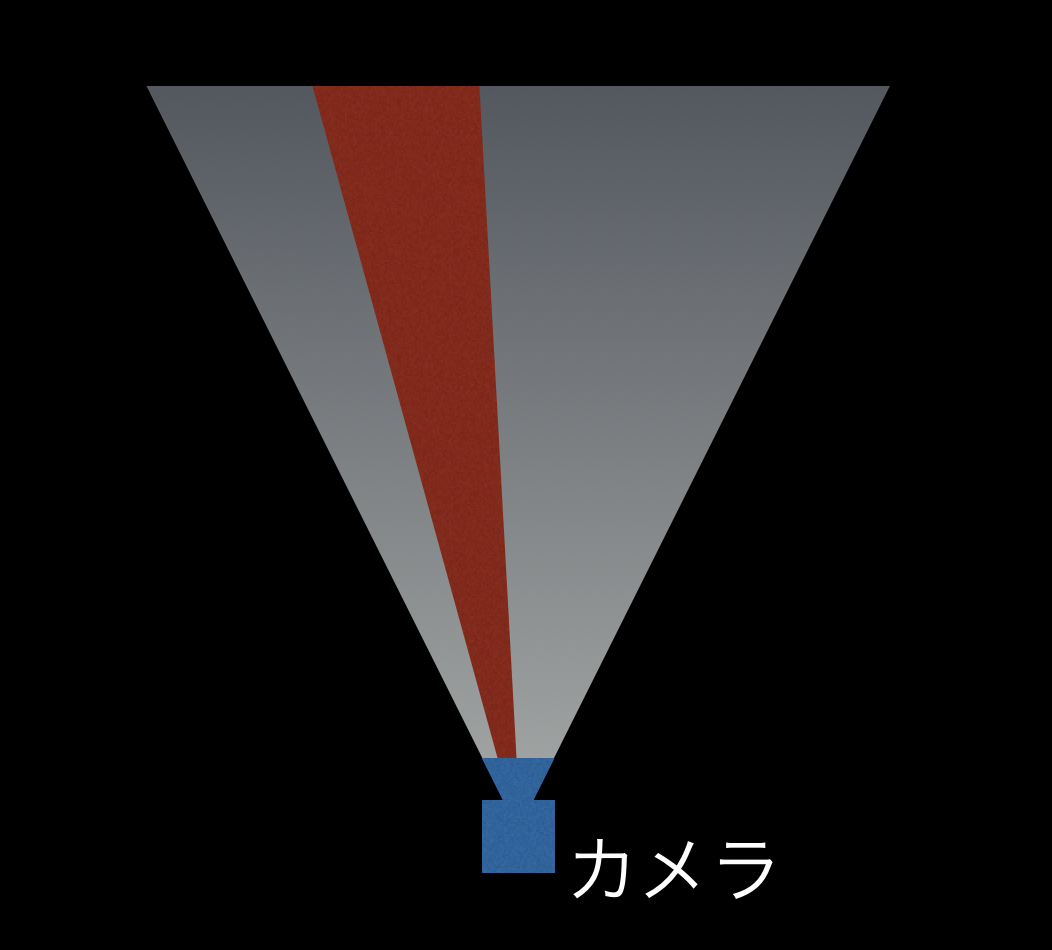
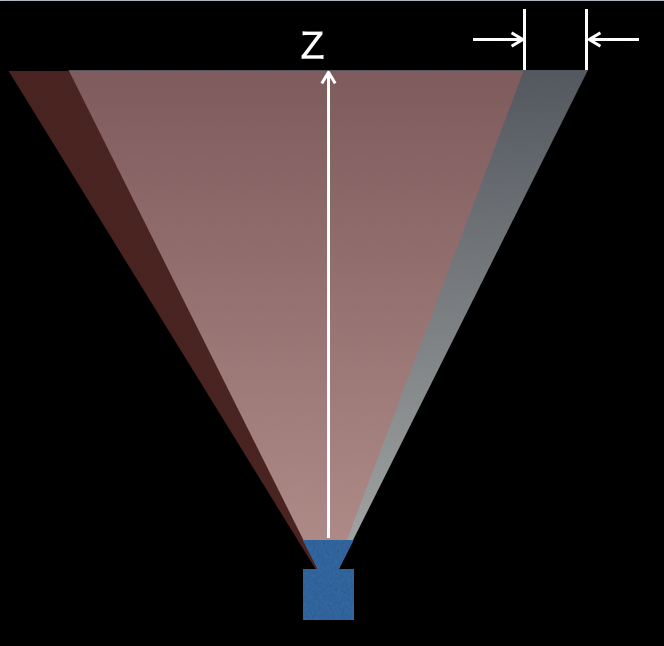
赤く示した部分が、斜めの投影です。通常の投影と違い、左右が非対称になっていますね。こうした描画をするために、Unityは特殊な関数を用意しています。
Camera.CalculateObliqueMatrix
それが Camera.CalculateObliqueMatrix です。ドキュメントから引用してみます。
Matrix4x4 CalculateObliqueMatrix(Vector4 clipPlane);
パラメーター
clipPlane クリップ平面とみなす Vector4
戻り値
Matrix4x4 斜めの近平面投影行列を返します。説明
計算し、斜めの近平面投影行列を返します。クリップ平面のベクトルを与えると、この関数はこのクリップ平面を近平面と決定するカメラの投影行列を返します。
引数にクリップ平面を渡すと行列を返すので、これを projection matrix に入れるんですね。なるほど、画角を狭めたカメラで目標を向いて、この関数で near clip 面を傾けるわけですね。
ですが今回はこれを使いません。鏡面や水面の反射を作るときは便利なAPIと思いますが、今回のように空間の一部を描画したい場合はもっと楽な方法があります。
通常の投影行列と斜めの投影行列の比較
せっかくなのでちゃんと理解する方針で行きましょう。まずは一般的な投影行列を見てみます。これはググるといくらでも出てきますね。
\begin{pmatrix}
\frac{2near}{right-left} & 0 & \frac{right+left}{right-left} & 0 \\
0 & \frac{2near}{top-bottom} & \frac{top+bottom}{top-bottom} & 0 \\
0 & 0 & -\frac{far+near}{far-near} & -\frac{2 far near}{far-near} \\
0 & 0 & -1 & 0
\end{pmatrix}
うん、ちょっとクラクラしますね。でもよく見ると、そんなに難しくはないのです。
たくさんある式のうち、
right+left \\
top+bottom
このふたつは通常の投影行列ではゼロになります。だって右の境界は左の境界の、符号反転ですから。上下も同様。ところが斜めの投影行列では、ここがゼロになりません。左右対称ではない、上下対称ではないとはそういうことですよね。
そして次に、
right-left \\
top-bottom \\
このふたつは、右の境界と左の境界の距離を意味するので、通常の投影行列だろうが斜めの投影行列だろうが同じになります。そして far および near に関連する項目も、通常の投影行列と斜めの投影行列で同じものになります。同じものは変更する必要がありません。
つまり!
斜めの投影行列は、通常の投影行列の
\begin{pmatrix}
□ & □ & A & □ \\
□ & □ & B & □ \\
□ & □ & □ & □ \\
□ & □ & □ & □ \\
\end{pmatrix}
このAとBだけを書き換えればよい!ということになります。(そして通常の投影行列ではABともにゼロでしたね)
目的に近づいてきましたよ。
投影行列にずれを加える
この「ずれ」の量ですが、図を見ると奥行き(Z)に比例した値になっていますね。これで、先ほどの行列のABが残ったわけがわかりました。試しにベクトルを掛けてみましょう。□はここでは気にしない部分です。
\begin{pmatrix}
□ & □ & A & □ \\
□ & □ & B & □ \\
□ & □ & □ & □ \\
□ & □ & □ & □ \\
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z \\
w \\
\end{pmatrix}
=
\begin{pmatrix}
□ + □ +Az+ □ \\
□ + □ +Bz+ □ \\
□ + □ + □ + □ \\
□ + □ + □ + □ \\
\end{pmatrix}
ほら、通常ではゼロのはずのAzやBzが加えられていますね。つまり、
Aはx軸(左右)にzに比例した値を加え、
Bはy軸(上下)にzに比例した値を加えて
いたわけです。
よってこのA,Bにずらす比率を入れるだけで、斜め投影行列は完成してしまうのです。わかってしまえば超簡単!
ソースコード
こんな感じになります。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class ObliqueManager : MonoBehaviour {
public Camera main_camera_;
public GameObject pane_go_;
private bool input_update(Camera camera, Transform tfm)
{
bool clicked = false;
var clicked_position = new Vector2(0f, 0f);
if (Input.touchCount > 0) {
clicked_position = Input.GetTouch(0).position;
clicked = true;
} else if (Input.GetMouseButton(0)) {
clicked_position = Input.mousePosition;
clicked = true;
}
if (clicked) {
Ray ray = camera.ScreenPointToRay(clicked_position);
var plane = new Plane(new Vector3(0f, 0f, -1f), tfm.position.z);
float distance;
if (plane.Raycast(ray, out distance)) {
var hit_pos = ray.GetPoint(distance);
tfm.position = hit_pos + new Vector3(-0.5f, 0.5f, 0f);
}
}
return clicked;
}
void Update () {
if (pane_go_ == null) {
return;
}
bool pressed = input_update(main_camera_, pane_go_.transform);
Debug.Log(main_camera_.projectionMatrix);
pane_go_.SetActive(pressed);
var tfm = pane_go_.transform;
var off_x = tfm.position.x;
var off_y = tfm.position.y;
var off_z = tfm.position.z;
//斜め投影行列設定ここから
var camera = GetComponent<Camera>();
camera.fieldOfView = Mathf.Atan(0.5f/off_z) * Mathf.Rad2Deg * 2f;
/* ↑ mine12345super さんの指摘のように fieldOfView は projectionMatrix を操作してしまうと
* その後の代入は無視されてしまうので、最初の一度のみが有効で以降は無駄な処理になっています
*/
var matrix = camera.projectionMatrix;
matrix.m02 = off_x*2f;
matrix.m12 = off_y*2f;
camera.projectionMatrix = matrix;
//斜め投影行列設定ここまで
}
}
前半は入力処理なので置いといて、後半の Update ですね。オフセットの値をmatrix[0,2] matrix[1,2](すなわちここがAB)に入れて、projectionMatrix に戻しています。だけ!驚くほどのシンプルさ。そして画角(fieldOfView)で窓の広さを決めています。
このカメラでRenderTextureに書き出したものを円形のメッシュに貼り付ければ、冒頭の画像のような効果を作ることができます。
まとめ
今回は Camera.CalculateObliqueMatrix を使わずに斜め投影行列を作ってみました。直接作ったほうが楽だし、演算が少ないので計算誤差の観点からも有利です。だけどもし空間上の鏡(ドライブゲームのサイドミラーとか)を表現したいときは、CalculateObliqueMatrix を使うのが便利だと思います。使い方はStandard Assetsから水面のサンプルなどを見てみるとよいでしょう。
そんではメリークリスマス!