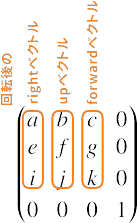今回は、ちょっとした行列の課題をなるべく丁寧に解説してみます。その過程で、CGに使用される行列についての理解を深めるのが目的です。
課題:ビュー行列からカメラ前方ベクトルを取得できる理由を明らかにする
Unityのシェーダでカメラの前方ベクトル(向いている方向)を得ようとした場合、
float3 forward = -UNITY_MATRIX_V[2].xyz;
または
float3 forward = -UNITY_MATRIX_V._m20_m21_m22;
のように記述することで得られます。これは、UNITY_MATRIX_Vという4x4行列のこの部分を取り出していることになります。

どうしてこれがカメラの向きになるのか?その理由を明らかにすること、これが今回のミッションです。
モデル行列の意味
物体の姿勢を表す行列はモデル行列と呼ばれ、4x4なので以下のような形をしています。

そしてこのように、4番目の行については (0, 0, 0, 1) であることが決まっています。

そしてこのモデル行列というのは、うまいことに行列の中に意味が残されています。

赤枠の部分が回転、緑枠の部分が移動を意味します。(赤枠部分にはスケール、つまり拡大縮小も入りますが、今回はスケールは考えません)
当たり前のようにも見えますが、行列になっても意味が残っているのは、けっこうな偶然とも言えます。順を追ってその理由を見ていきましょう。
移動と回転を独立させる
行列はベクトルに掛けることで具体的な(直感的な)意味を持ちます。たとえばベクトル$(p_{x}, p_{y}, p_{z})$に行列を掛ける式はこうなります。
ごちゃごちゃしていますが右辺もベクトルです。行列を掛けるとベクトルはこうなるんです。
さてここで、移動だけの行列を考えてみます。上の式の結果つまり右辺が
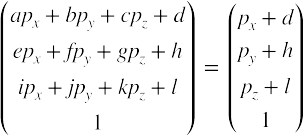
この右辺のようになれば移動だけをしたことになりますよね。ここから aを1にすればいい、bとかcをゼロにすればいい、と考えていけます。(数学的には「恒等式なので係数が定まる」とか言います)
結果、$(d, h, i)$ を足すだけの移動行列というのは、$a=f=k=1$, $b=c=e=g=i=k=0$ としてこうなります。

次に回転行列については、行列の効果から移動を取り除いたもの、と考えましょう。移動成分は d, h, i だったので、これらをゼロにします。
結果、回転行列というのはこうなります。

移動と回転の行列計算
モデルを変換する際に、回転と移動は同時にはできないとして。先に実行するとしたら、どちらを先にするのが適切でしょうか?
数学的には「どちらかに決めさえすればどっちでもいい」のですが、ゲームや3DCGなど、人間の感覚を尊重する場合は明らかに「回転してから移動する」のが望ましいです。「いまどこにいるか?」が移動量だけを扱えば良いことになりますから。(ここは納得するまで考えるべきポイントです)
さて、行列の掛け算の順番の注意ですが、ベクトルを右からかけるので、右にある方が先に計算されます(=右にある方が先にベクトルへ効果を及ぼします)。
移動行列を $T$ 、回転行列を $R$ 、変換前のベクトルを $p$ とすると$TRp$としたいので、
こうなります。

赤枠の回転行列が先に掛けるべきもので、右側にあるのを確認してください。
この二つの行列 $TR$ を行列の掛け算として律儀にネチネチと計算すると、ちゃんとこうなります。
行列の掛け算は面倒ですが、上の計算は人生で一度ぐらいはノートなどで実際にやるべきところです。モデル行列の内部の意味がちゃんと残っているのは全くもって幸運だな、と感じられるでしょう。回転と移動の順番を逆にするとこうはなりませんから。
回転行列から進行方向(前方ベクトル)を取り出す
モデル行列は納得できました。ここで移動量は、緑枠の部分が移動ベクトルそのものでした。では、回転行列からなにか情報を取り出す方法を考えてみます。
これはちょっと気付きにくいのですが、話は単純で、回転行列は何かを回転させているわけなので、物体の進行方向ベクトル (0, 0, 1) を回転させたものというのは、回転後の進行方向になりますよね。
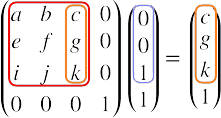
これも手で計算してみるとよくわかります。x要素とy要素がゼロ、z要素が1の進行方向ベクトルをかけると、$c, g, k$ の部分を取り出したことになるわけです。
つまり、物体の進行方向のベクトルというのは、モデル行列の $c, g, k$ すなわちシェーダ上では
float3 forward = M._m02_m12_m22
で取得できることになるのです。これは知っていると必ず役に立つ知識です。
同様に、(1, 0, 0)および(0, 1, 0)を掛けてみると、回転行列は具体的な意味を持つ3つのベクトルで構成されていることがわかります。
なかなか興味深い事実ではないでしょうか。ここは「ああ、そりゃそうか」という気持ちになるまでじっくりと考えたいところです。一度でも納得すれば、残りの人生はずっとその理解を財産にして生きていけます。
UNITY_MATRIX_V とは
そろそろ課題に戻っていきましょう。UNITY_MATRIX_Vですが、これはビュー行列(view matrix)と呼ばれるもので、カメラの位置と姿勢を示す行列です。
ただし気をつけなければいけないのは、ビュー行列は、モデルの変換行列とは大きく異なる点があることです。
ビュー行列とは
モデル行列を$M$、ビュー行列を$V$とすると、ベクトルと$p$の乗算としては
$VMp$
のようにモデル行列のあとに$V$をかけることになります。(さきほども触れた通り、右にある$M$が$V$より先に効果を及ぼします)
ここで、カメラの位置および回転を適用する、ということは、世界全体をカメラの位置および向きに持ってくる、ということです。
考え方が逆なのです。
なので、ビュー行列の$V$は、移動と回転で作ったモデル行列の、その逆行列になっています。逆行列になっています!
これがモデル行列とは大きく異なる点です。transformのPositionやRotationから構成されている点は同じなのです。
逆行列とは
まず単位行列を知る必要があります。掛けても何も起きない行列、数字で言うと1みたいな行列が単位行列です。つまり
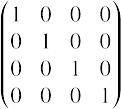
これが4x4の単位行列になります。$I$と表記されることが多いですね。
逆行列は、ある行列に掛けると単位行列になる行列のことです。掛けると1になるということで、逆数みたいなものですね。
行列 $M$ の逆行列を $M^{-1}$とするとこうなります。
$M^{-1}M=I$
一般的に、逆行列というのはけっこう大変な計算になります。ちなみに2x2の逆行列はこうなります。

3x3は、どえらいことになります。例えばこちらにありました。https://risalc.info/src/inverse-cofactor-ex3.html 一度は眺めて、げんなりしておきましょう。
移動行列の逆行列
さて、移動行列の逆行列を考えてみます。4x4の逆行列は想像するだに恐ろしいですが、実はこれは何も難しくはなくて、平行移動の反対は符号を反転するだけで良いのです。
移動したぶんを戻せばいいわけですから、直感的にも納得できます。
回転行列の逆行列
問題はこちらなのですが、ここに数学の恐るべきトリックがあります。
回転行列の逆行列は転置行列と一致する(ババーン)
逆行列が転置行列と一致する行列は直交行列と呼ばれています。回転行列は直交行列なのです。
なお転置行列というのは単に行と列を入れ替えたもので、逆行列とは違って簡単に算出できます。
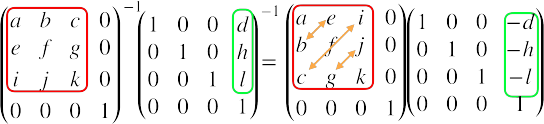
つまり、回転行列の逆行列はこうなります。
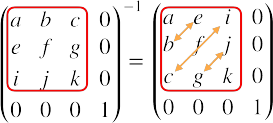
eとb、iとc、jとgをそれぞれ入れ替えています。要するに転置しているだけ、これで逆行列が得られてしまうのです。なんという僥倖。
ビュー行列を作ってみる
では、カメラの移動と回転からビュー行列を作ってみましょう。
移動Tと回転Rから得られる通常のモデル行列は
$TR$
これの逆行列を求めればいいので、ビュー行列はこうなります。
$V=(TR)^{-1}$
逆行列の計算は行列の性質から順番が入れ替わり、
$V=(TR)^{-1}=R^{-1}T^{-1}$
これと上で述べた、移動行列と回転行列の逆行列から、こうなります。
手間を惜しまず右辺の掛け算を計算してみると、赤枠の回転部分については保存されるのがわかります。
ただし緑枠の移動部分については保存されません。値の変わってしまう移動部分については $?$ としておいて、こうなります。
これがビュー行列の正体、ということになります。
まとめ
というわけで、ビュー行列の正体がわかりました。ではなぜカメラの向いている方向が
float3 forward = -UNITY_MATRIX_V._m20_m21_m22;
これで取れてしまうのか?どうして、ビュー行列の2行目の0, 1, 2列を取り出すとカメラの向きになるのか?
さきほどの「回転行列から進行方向(前方ベクトル)を取り出す」の章で、$(c, g, k)$が回転後の前方へのベクトルだったことを思い出してください。
つまりビュー行列から$(c, g, k)$を取り出す方法を見つければ良いのです!というわけで

これ。カメラの進行方向ベクトルが、ビュー行列にたまたま残っている!
・・・という、そんな理屈だったわけです。けっこうすごくないですか?
同様の理屈でカメラのupベクトルも取り出せますね。実は僕もこれに気づかず、upベクトルをuniformで渡したりしてた時期がありましたが、ビュー行列から取り出したほうがエレガントですね。
めでたしめでたし。
おまけ
float3 forward = -UNITY_MATRIX_V._m20_m21_m22;
なんでマイナスがついてるのか?
これは座標系の違いを吸収しているためです。理論を構築する上での意味はないので、追求しません。
なおUnityの描画時のZ軸方向については、プラットフォームごとに
#ifdef UNITY_REVERSED_Z
で区別可能な方式の差がありますが、前方ベクトルのマイナス符号については、これとは関係ありません。