らせん状にマスを埋める複素数列と戯れる

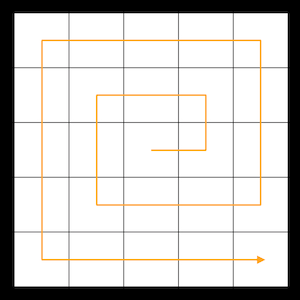
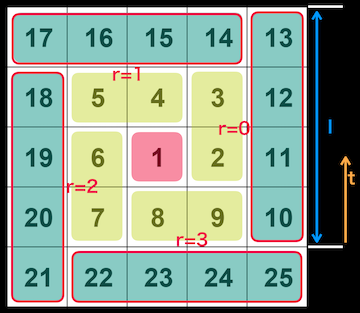
ゲームなんかでわりとよくある話だと思いますが、正方形のマスが並んでいるとして、中央からグルグルと回して全てのマスを巡回するパターン。これをプログラムで作ろうと思うとけっこう面倒なことに気がつきます。

こんな感じに、中心からスタートしてマスを埋めていきたいわけです。
今回は、複素数を駆使してこれの一般項を出してみようと思います。

#一般項
結論から述べれば、n番目の位置を示す複素数$a_{n}$の一般項はこうなります。

$a_{n}=\left(\left[N-1\right]+\left[\left(2-N+\left(n-\left(2N-3\right)^2-1\right)\right)\bmod 2(N-1)\right]i\right)i^{floor(\frac{n-(2N-3)^2-1}{2(N-1)})}$

ただし $N=ceil(\frac{\sqrt{n}+1}{2})$
$floor(x): xを整数で切り捨て$
$y\ mod(x): yを整数xで除算したときの余り$
$ceil(x): xを整数で切り上げ$

Nは実数ですが全体が複素数でできているので、プログラムに落とす際は複素数演算の実装が必要です。
見るからに大変な式ですが、順を追って導出していきましょう。

#複素平面
$i$ を虚数単位として、
$a+ib$
こんな形を複素数と呼びます。複素数についてはわかりやすい資料がたくさんあるので詳細は省略。
「クォータニオン完全マスター」という動画でも解説があります。
https://youtu.be/uKWLPU8gfIY?t=1294
複素数の説明は、動画のこの位置から10分間です。

#いざ解析

##番号を振って観察する

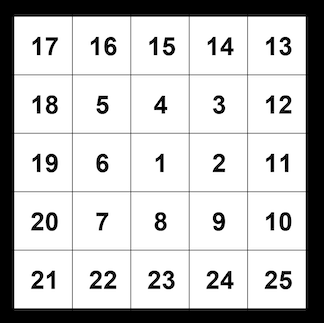
番号を振ってみましょう。1番が中央にあるとして、こうなります。

数字がらせん状に増えているのを確認していただければ。

##パターンを見出す

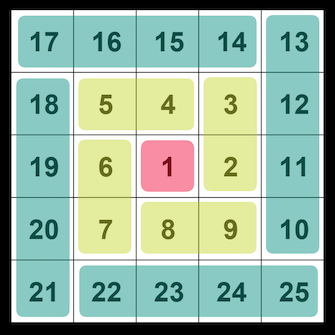
ここからパターンを見つけます。色々な分け方があると思いますが、ここで道を間違えるとヒドい目にあいます（あいました）。センスが問われるところですね。今回は、こんなエリアに分割して考えます。

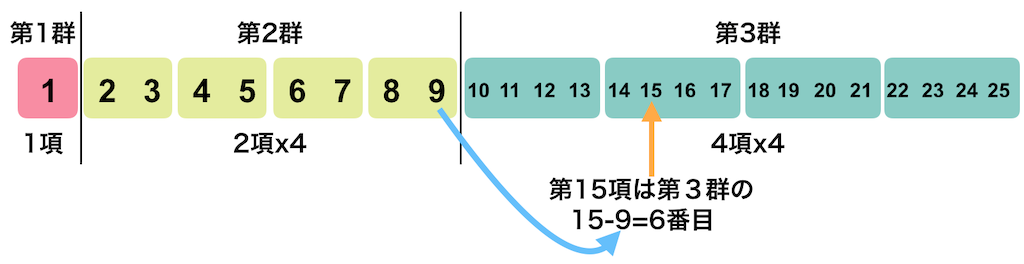
横一列に並べると、

こんなパターンになります。これは数列のタイプとして「群数列」と呼ばれるものになります。

##群数列に分ける

ここで色分けしている部分を「群」とすると、含まれる項数と群の関係はこうなります。

項数がx４となっているのは正方形が４辺だからなのは明らかですね。ここはどこまで項が大きくなってもx4です。

##群に含まれる項数を求める
この先を調べてみると、第４群には6x4、第５群には8x4の項数が含まれることがわかります。よって

$第Ｎ群に含まれる項数=2(N-1)×4=8(N-1)$ ・・・(1)

と表せます。決して難しくはないので、ぜひ納得していただきたいところです。ただし、$N=1$のときは例外で項数は１であることに注意します。

##N群には何項目が来るのか

知りたいのは、第N群に差し掛かっているときに頭から数えて何項目なのか、です。つまり、等差数列であるところの(1)式の和を求めることになります。

##まず群の終端について調べる

第Ｎ群の終端にある第$n_{f}$項は、
第１群が例外だったことを思い出して、第２群から第N群までの和を公式から求め、そこに第１群の1を足します。
$n_{f}=\frac{8+8(N-1)}{2}(N-1)+1=4N^{2}-4N+1=(2N-1)^{2}$ ・・・(2)
これを解くと、$n_{f}$項が属する群Nは
$N=\frac{\sqrt{n_{f}}+1}{2}$
となります。

###余談
$N$は整数なのに式に平方根が含まれるのが気持ち悪くありませんか。実は$\sqrt{n_{f}}$は必ず整数（さらにいえば奇数）なのです。つまり$N$群の最後の項というのは、必ず平方数になっているのです！！いやあ、数学の神秘ですねえ・・・いえ、実はこれは当たり前で、もともと正方形になる形を考えていたことを思い出すと、なんの不思議もないんですよね（上の図を確認してください）。ははは。でもこういったことで納得していくと、数式に誤りがないことを検算したことになるでしょう。

##群の終端から任意のn項の群を求める

そして、終端とは限らないnについては、Nが整数であることから上式を整数に切り上げることで求められます。
$N=ceil(\frac{\sqrt{n}+1}{2})$
（ただし$ceil$は整数未満を切り上げる関数）
これで任意のn番目の項目が属する群が求められるようになりました。

##群の中で何番目なのか
次に、いま注目しているn項が群の中の何番目に位置しているかを求めます。
これは、nから一つ前の群の総数を引くことで求められます。

求めたい「何番目か」をmとすると、(2)式で最終項の群を求められるのでここに(N-1)を入れて
$m=n-(2(N-1)-1)^{2}=n-4N^2+12N-10$・・・(3)
これが何番目か、になります。

##現在の辺に含まれる項目数
(1)式より、第Ｎ群には $8(N-1)$個の項目が含まれています。正方形の一つの辺に含まれる項数lは
$l=8(N-1)/4=2(N-1)$・・・(4)
となります。

##どの辺にいるか・辺の中のどこにいるか
式(3)および式(4)より、４つの辺のうちどこにいるか（0, 1, 2, 3のいずれか）は$m$を$l$で割った値で算出できます。この値を$r$とすると
$r=floor(\frac{m}{l})$
こうなります。$floor$は小数点以下の切り捨てを行う関数とし、結果は必ず整数になります。

その辺の中のどの位置か、は$m$を$l$で割った余りで算出できます。この値を$t$とすると
$t=m \bmod l$
こうなります。$m \bmod l$は $m$を$l$で割った余りで、これも必ず整数です。

##ここまでの結果

第何群にいるか、の$N$、その群の中での位置$m$がわかることで
どの辺にいるか、の$r$
辺のどの位置にいるか、の$t$
がわかりました。

##辺のスタート位置を求める・前編
ここまでは普通の数列の話でしたが、ここからは複素数を活用していきます。

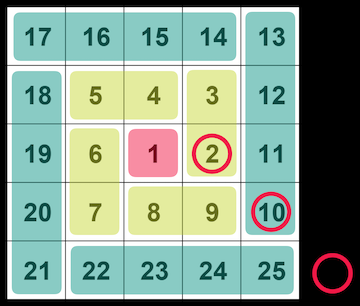
求めたいのはこの赤い丸の位置です。これを複素平面で考えるとこうなります。

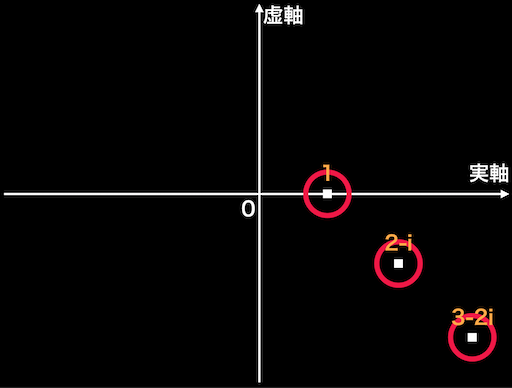
いったん複素数で表現してしまえばとてもシンプルで、これなら数列の初歩を理解していれば一般項を出せますよね。辺０の開始位置$s_0$を複素数として
$s_0=(N-1)-(N-2)i$
と表すことができます。

##辺のスタート位置を求める・後編

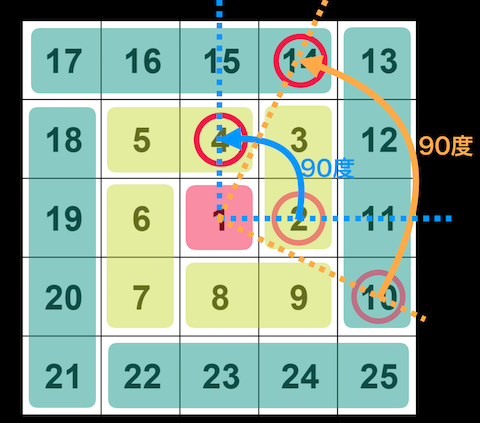
問題は他の辺ですが、これは原点を中心に回転させればよく、その角度は90度です。$i$をかけることで90度回転することを思い出せば、辺の位置(0,1,2,3のどれか)を$r$とすれば $i^r$を掛ければ良いことがわかります。
よって開始位置$s_r$は
$s_r=s_0 i^r = \left[(N-1)-(N-2)i\right]i^r$
これで算出できました。単純明快、これが複素数の威力です。

##進行方向を求める
ここまで理解していればこれは簡単です。

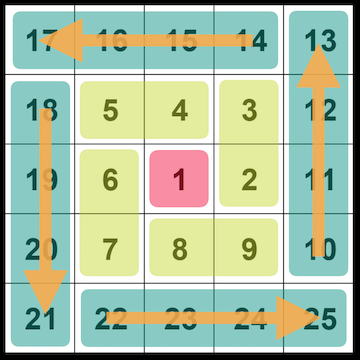
辺０番の進行方向は真上、すなわち$i$です。
辺０番の進行方向：$i=i^1$
辺１番の進行方向：$-1=i^2$
辺２番の進行方向：$-i=i^3$
辺３番の進行方向：$1=i^4=i^0$
なので、進行方向$d_r$は
$d_r=i^{r+1}$
となります。

##ついに一般項へ
辺の開始位置がわかり、進行方向がわかり、進行ステップ数がわかっているので、もう難しくありません。
すべての情報を結集し、一般項$a_n$を求めます。

$a_n=s_r+td_r$
ただし
$d_r=i^{r+1}$
$s_r=\left[(N-1)-(N-2)i\right]i^r$
$t=m \bmod l$
$r=floor(\frac{m}{l})$
$m=n-4N^2+12N-10$
$l=2(N-1)$
$N=ceil(\frac{\sqrt{n}+1}{2})$

以上です。N以外の記号を展開すると、冒頭の式になります。
プログラムを書く際は複素数の掛け算や足し算を実装し、最終的に得られた値の実部をx軸、虚部をy軸に取ることで描画することができます。

#Hexmapへの応用
同じ理屈で、hexmapにも対応してみましょう。
やはり中央から始まって、グルグルと回りながら平面を充填するパターンを考えます。

正方形と同様に群数列を見出します。
（実は正方形での群数列の作りも、同じアルゴリズムで六角形に対応する目標があってああなっています。）

群数列はこうなります。x6に六角形の特徴が出ていますね。

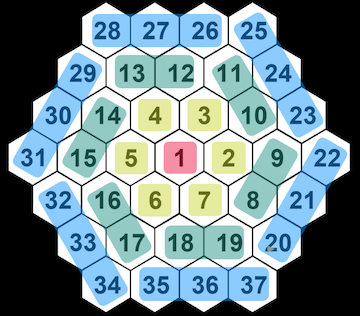
手順は省略しますが正方形と同じやり方、同じ順番でひとつずつ問題をクリアしていくと、一般項はこうなります。

$a_n=s_r+td_r$
ただし
$d_r=(\frac{1}{2}+\frac{\sqrt{3}}{2}i)^{r+1}$
$s_r=(N-1)(\frac{1}{2}+\frac{\sqrt{3}}{2}i)^r$
$t=m \bmod l$
$r=floor(\frac{m}{l})$
$m=n-3N^2+9N-8$
$l=N-1$
$N=ceil(\frac{1}{2}+\frac{\sqrt{3}}{6}\sqrt{4n-1})$

それぞれの記号の意味は正方形版と同じです。

#プログラム例
サンプルコードをpythonで記述してみました。
python は組み込みで複素数型 complex があり、演算も可能です。

import math
def getRectProgression(n):
    if n <= 1:
        return complex(0, 0)
    #end
    N = int(math.ceil((math.sqrt(n)+1)/2))
    m = n - (2*N-3)*(2*N-3) - 1
    l = (N-1)*2
    r = int(m/l)
    t = m % l
    ir = complex(0, 1) ** r
    irt = ir * complex(0, t)
    s0 = complex(N-1, -N+2)
    s = s0 * ir
    a = s + irt
	return a

上記が正方形版の一般項になります。

import math
def getHexProgression(n):
    if n <= 1:
        return complex(0, 0)
    #end

    N = int(math.ceil(0.5+(math.sqrt(3)/6)*math.sqrt(4*n-1)))
    m = n - 3*N*N + 9*N - 8
    l = N-1
    r = int(m/l)
    t = (m % l)*math.sqrt(3)*0.5
    i = complex(0.5, math.sqrt(3)*0.5)
    ir = i ** r
    ir1 = i ** (r+1)
    ir1t = complex(t,0) * ir1
    s0 = complex(math.sqrt(3)/2 + (N-2)*(math.sqrt(3)/4), -(N-2)*3/4)
    s = s0 * ir
    a = s + ir1t
	return a

上記が正六角形版の一般項になります。
いずれも、nに正の整数を入れると複素数で位置座標を返します。

#ギャラリー

矩形

hexagon

通路の幅が一定の迷路を生成

完全に連続しているので光点をずっと追っていけます

#まとめ
ま、矩形マスでらせんを描きたいと思ったら、普通は一般項なんて求めずにプログラムの条件分岐などで作ってしまうものと思います。でも一般項を出してしまえば、ものすごく大きな第$n$項であっても一定の時間で算出できますし、数式は具体的な言語で記述されたコードよりも汎用性が高いので、恒久的に使えるのではないでしょうか。

複素数はどちらかといえば地味な概念で、クォータニオンに比べればプログラミングで登場することもそんなにないと思うのですが、強力なツールになる例もあるよね、という話でした。